Rechenstäbe, -schieber,
-scheiben,
-zylinder, -walzen und -tafeln
|
Bereits kurz nachdem Lord Napier 1614
seine Logarithmentafel veröffentlicht hatte, konstruierte
►Edmund Gunter
1624 eine logarithmische Skala, auf der Proportionen
mit einem Zirkel abgegriffen und an eine andere Position übertragen
wurden. Die Skala wurde zunächst auf einen Rechenstab oder auch
auf einen
Proportionalzirkel aufgebracht.
In der Regel reichte sie von 1 bis 100 über zwei Größenordnungen.
Bereits 1632 konstruierte
William Oughtred eine Rechenscheibe mit einer einzelnen kreisförmigen Endlosskala und zwei verstellbaren
Zeigern, die den Zirkel ersetzten.
Rechenscheiben erreichten zunächst
keine große Verbreitung. In England setzte sich der
Rechenschieber vom Typ "Sliding Gunter" durch: zwei
gegeneinander verschiebbare Stäbe mit Gunterskalen oder alternativ
einer Zunge in einem Körper aus zwei Leisten. Der erste, der dafür
eine standardisierte Form definierte, war
James Watt. Im 19. Jahrhundert kam
der Läufer dazu, der es ermöglichte, Werte auf nicht
benachbarten Skalen einander zuzuordnen. In dieser Form wurde der
Rechenschieber zum Standard-Handwerkszeug des
Ingenieurs. Rechenschieber
sind meist nicht für eine spezielle Anwendung, sondern für allgemeine
technische oder kaufmännische Multiplikations- und Divisionsaufgaben optimiert. Den Weg in
die
►Lehrpläne
allgemeinbildender Schulen in Deutschland fand der
Rechenschieber erst nach dem ersten Weltkrieg.
►Ausführliche
Geschichte
►Einführungsvideo.
►Lehrbuch
►When
Slide Rules Ruled |
||
|
|
Gunter
Rule Buchsbaumlineal 24 Zoll zum Messen und Rechnen Logarithmische Skalen 1624 zunächst auf Sector später als Lineal mit 22 Skalen Bis ins 19. Jahrhundert Hilfsmittel zur Navigation Ohne Herstellermarkierung Großbritannien ca. 1830 |
vorn: Logarithmische Skala Num von 1 bis 100,
außerdem Skalen Sin, Tan, S*R, T*R, V*S und Meri und Eq Parts (für
Mercatorkarten).
hinten: lineare Zollskala von 24 bis 0, darunter links lineare Skala von 10 bis 0 mit Hilfslinien zum Abgreifen dezimaler Zwischenwerte, rechts Lea (lineare Bezugsskala), Cho (Grad), Rum (Kompassmarken 90°=8 Rumb), Sin, Tan, S*T, M*L (Miles of Longitude, Abstand zweier Längengrade gegebener Breite), Cho. ►Ähnliche Geräte ►Anwendung ►Gunter Rules in Navigation |

|
Pes mechanicus artificialis oder neu erfundener Maß-Stab a) Variante mit Zirkel b) Variante mit zwei Stäben Michael Scheffelt 1699 / 1718 Reproduktion R.A. 2019 |
Quadratstab, 1 Ulmer Schuch (289 mm) lang 6-Zoll-Skala in Zwölftelteilung,dazu Gradskala, 10-Zoll-Skala in Zehntelteilung, dazu Quadrat-, Kreisflächen-, Kubikskala doppelte Gunterskala zum Rechnen dazu Sinusskala von 35' bis 90° und Tangens-Skala von 35° bis 45° ►Scheffelt: Pes mechanicus ►Scheffelt: Instrumentum proportionum ►The oldest German Slide rule |
 |
Curieuser Rechen=Stab Rechengerät entworfen von Jacob Leupold 1727 im "Theatrum Arithmetico-Geometricum" nach einer Beschreibung von Seth Partridge von 1661 Reproduktion R.A. 2016 |
Leupold liefert Anleitungen zum Nachbau, darunter Scheffelts Pes
mechanicus artificialis zum "Rechnen auf Linien mit Zirckel" und ein
doppelseitiger
Rechenschieber zum ´"Rechnen auf Linien ohne Zirckel" Lineare Skala 12 Zoll in Zehntelteilung Logarithmische Skala, 2 Dekaden 1..10..100 Sinusskala, Tangensskala Gradskala ►Leupold: Theatrum Arithmetico Geometricum ►The oldest German Slide rule |

|
Carpenter's slide rule / Timber rule / Polymeter nach Henry Coggeshall 1677 Dieses Exemplar: Stanley Rule & Level Co. New Britain Conn. USA ab 1857 - 1920 $ 0,92 (1914) Näheres |
Klapp-Zollstock für Zimmerleute 2 mal 12 Zoll. Die ausziehbare Zunge des einen Schenkels enthält eine logarithmische Skala von 1 bis 100 Darüber findet sich das Gegenstück, darunter eine verschobene Skala von 4 bis 40 zur Berechnung des nutzbaren Holzanteils in Baumstämmen. Der zweite Schenkel enthält Hilfsskalen zum Verhältnis von Länge und Breite von Brettern. die Rückseite dient als Zollstock. ►sliderules.info ►Buch "Polymeter" |

|
Excise officer's slide rule nach Thomas Everard 1683 "Stereometry made easie" Ohne Herstellermarkierung Großbritannien vor 1824 ►Fassberechung Gebrauchsanweisung |
12 Zoll langer Vierseiten-Rechenschieber: Er enthält mehrere logarithmische Skalen 1..10, eine Reversskala zum Dividieren und eine doppelt lange Skala zum Wurzelziehen. Außerdem zwei experimentell ermittelte Prozentskalen, die den Steuerbeamten (Excise officer) zur Berechnung des Inhalts nur teilweise gefüllter liegender oder stehender Fässer dienten. ►Rechenschieber.org ►mechrech.de ►sliderules.info ►Nathan Zeldes ►Download des Everard-Buchs |

|
Excise officer's slide rule Spätere Form Dring & Fage London Tooley Street zwischen 1824 und 1849 ►Fassberechung Gebrauchsanweisung ►Weiterentwicklung |
10 Zoll langer zweiseitiger Rechenschieber mit zwei Zungen, die zu einer
Doppelskala
kombiniert werden können. Der Rechner besitzt die gleichen
Skalenpaare wie der Everard-Typ. Messingstifte bezeichnen "Gauge Points" z.B. für "ImG". Dieser Punkt markiert den Durchmesser eines 1 Zoll hohen zylindrischen Behälters mit dem Volumen von 1 Gallone. Mit dem Rechenschieber kann man auf andere Zylinderhöhen oder Durchmesser umrechnen. ►sliderules.info ►mathsinstruments ►sliderulemuseum ►Tom Martin |

|
System Soho James Watt um 1800 ►Soho-Varianten Version Lenoir ab 1825 ►Animation John Farey 1827 Näheres Nachbau R.A.2023 |
Frühe Geräte mit logarithmischen Skalen richteten sich an Praktiker:
Landvermesser, Zimmerleute, Seeleute
oder Steuereinnehmer.
Für Ingenieure mit hohen Qualitätsansprüchen entwarf um 1800
James
Watt einen Standard-Rechenschieber nach dem System Soho
mit einfachem Layout und nur wenigen, aber sehr exakt gravierten Skalen.
Die besten Soho-Rechenschieber kamen später aber aus Frankreich, wo die Instrumentenbauer ►Lenoir 1825 eine vollautomatische Maschine zum Gravieren logarithmischer Skalen entwickelt hatten. |
 |
System Mannheim A.W. Faber (►350) ab 1892: gedruckte Skala Tavernier-Gravet ab 1890 ab 1825 gravierte Skalen Dennert & Pape Typ 109 ab 1888 Zelluloidskala A.W. Faber (►367) 1899 Stellenmerkzeiger |
Lenoirs Nachfolger
►Tavernier-Gravet propagierte ab 1851 das neue Layout
von Amédée Mannheim: Ein Läufer verknüpfte das obere mit dem unteren Skalenpaar.
Die Zunge bekam auf der Rückseite je eine Sinus-, Tangens- und
Mantissenskala. In Deutschland produzierten ab 1872 Dennert & Pape
(Aristo) Rechenschieber nach dem System
Mannheim. 1878 nahm auch Albert
Nestler die Produktion
auf. Wie vor ihm Lenoir entwickelte er eine
►automatische
►Graviermaschine.
Bei den ersten Modellen von A.W. Faber waren 1892 die Skalen
noch auf Holz gedruckt.
Ab 1888 beschichteten D&P das Holz mit
Zelluloid.
►Faber-Datierung ►Sliderules through Time |
 |
System Rietz Wichmann OEM Nestler 1908 ohne CI und ST Gebrauchsanweisung A.W. Faber 51/87 1935 Faber-Castell 1/87 1954 Schichtholzaufbau Aristo Scholar 0903 ca.1963 10 Skalen einseitig |
Beim
System Rietz von 1902 wurde eine Kuben- skala K integriert, die
Mantissenskala L auf die Vorderseite verlegt und
an den Schmalseiten zwei Lineale für cm und 1:25 hinzugefügt. Später kamen die
Inversskala CI
und die ST-Skala für kleine Winkel dazu. Dieser Aufbau
wurde für einige Jahrzehnte zum Standard - vor dem Krieg auf Körpern
aus Schichtholz mit federnder Gleitfuge und später vorwiegend in Kunstoff. Anwender Anleitung Rietz+Darmstadt ►Altersbestimmung ►sliderulemuseum ►Lob des Rechenschiebers |

|
Elektrotechnik Nestler No. 32 Electro 1908 Anleitung (No. 37) Faber-Castell 378 Elektro 1925 Reiss Elektro 1960 Faber-Castell Elektro 111/98 1965 Anleitung |
Ab 1905 erschienen immer mehr Spezialausführungen. Die Version
"Elektro" bot Skalen zur Berechnung des Gewichts und
Spannungsabfalls von Leitungen aus Querschnitt und Länge. Die
zunächst verwendeten Skalen über 4 Dekaden (0,1 bis 10000) wurden
später von LogLog-Skalen abgelöst, mit denen auch gebrochene
Potenzen bestimmt und der
Wirkungsgrad von Motoren und Dynamos berechnet werden konnte.
►Elektro-Rechenschieber ►Modellvergleich |

|
Wirtschaft A.W.Faber 307 Columbus System Rohrberg 1929 (für Schüler) ->342 Albert Nestler No. 40 ca. 1935 für Kaufleute Faber-Castell 1/22 ca. 1940 Disponent |
Der Nestler Typ 40 (ab 1913) und der Faber-Castell 1/22 "Disponent"
verzichteten auf Trigonometrie und besaßen dafür Marken und Skalen
zur Umrechnung englischer Maße und Geldbeträge auf kontinentale
Äquivalente. Mittels einer um den Faktor 3,6 verschobenen Skala
konnte man mit einer einzigen Einstellung taggenaue Zinsen
bestimmen. Zinseszins wurde zunächst mit Tabellen, später mit Log-Log-Skalen
bestimmt. ►Katalog ►Vortrag mit Folien ►Nestler |
 |
Darmstadt und Duplex Nestler Typ 21 1936 Darmstadt 13 Skalen Aristo Studio 0868 1949 24 Skalen 12,5 cm lang (auch in 25 oder 50 cm) Castell Schul-D-Stab 19 Skalen 1965 Reiss Progress 1968 14 Skalen |
1935 wurde das System Darmstadt definiert. Es platzierte auf der Rückseite der Zunge drei Log-Log Skalen und
verlegte die Trigonometrieskalen auf die Schmalseite. So konnte man bei klassisch einseitigem Schichtholz-Aufbau
13 Skalen unterbringen. Ab den 50-er Jahren ermöglichte der Einsatz von maßhaltigen Kunststoffen und Aluminium immer individuellere doppelseitige Layouts und die Unterbringung von immer mehr Skalen: Log-Log-Skalen wurden zum Standard; inverse und gefaltete Skalen und der Wechsel zwischen Vorder- und Rückseite verringerten die Zahl der Neueinstellungen bei längeren Rechenwegen. |
|
Letzte Generation Faber-Castell 2/83N 1969 Novo-Duplex 30 Skalen Reiss Duplex 3227 1968 mit Hyperbelfunktionen 30 Skalen, Anleitung Aristo 0969 StudioLog 1969 31 Skalen Anleitung ►Animationen |
Gegen Ende der 1960-er Jahre, als schon die ersten elektronischen Arbeitsplatzrechner erschienen, brachten die großen Hersteller noch eine Generation von Rechenschiebern "für Maschinen- und Elektroingenieure" heraus, die das Konzept bis an die Grenzen der Handlichkeit ausreizte. Doch es nützte nichts: Elektronische Bauteile wurden kleiner, ihre Möglichkeiten dagegen immer größer. 1972 erschien der elektronische HP-35. Er bot mehr Funktionen als jeder Rechenschieber bei höherer Genauigkeit. Den Herstellern von Rechenschiebern blieben nur ►Rückzugsgefechte. |
 |
Retro-Statussymbol Skalenlänge 4 cm Vernon Industries GB Nach 1975 |
Im Computerzeitalter wurde der Rechenschieber unter Ingenieuren zum Symbol für die gute alte Zeit: Hier eine Krawattennadel als funktionsfähiger Rechenstab mit Skalen A,C,D zum Multiplizieren, Dividieren, Quadrieren. |
| Rechenscheiben: Die gerade Skalenanordnung bei Rechenstäben und -schiebern birgt ein Problem: Viele Rechnungen führen zu einem Überschreiten der Dekadengrenze. Ein Verhältnis, das auf dem Rechenstab innerhalb der logarithmischen Skala von 1 bis 10 mit dem Zirkel abgemessen wird, endet bei einer Verschiebung außerhalb dieser Skala. Nach Einstellung der Faktoren auf dem Rechenschieber ragt die Zunge links oder rechts heraus, sie muss "durchgeschoben" werden von der 1 auf die 10. Rechenstäbe besitzen deshalb oft zwei Dekaden: die Skala erstreckt sich von 1 über die 10 zur 100. Dadurch sinkt aber entweder die Ablesegenauigkeit oder es steigt die Länge des Rechenstabs. Die einfachste Lösung ist hier, in die Breite zu gehen und die Skala kreisförmig und damit unendlich lang zu machen. So entsteht eine Rechenscheibe oder ein Rechenring. Die Klassifizierung der geraden Geräte in Rechenstäbe (plus Zirkel) und Rechenschieber (mit zwei gegeneinander verschiebbaren Skalen) wird bei den Rechenscheiben durch eine dritte Gruppe erweitert: eine Skala mit zwei drehbaren Zeigern (Oughtred), zwei gegeneinander verstellbare Skalen (Palmer), oder eine drehbare Skala mit einer festen Marke und einem einstellbaren Zeiger (Boucher). | ||
 |
Circles of Proportion William Oughtred 1632 Reproduktion R.A. 2019 ►Animation |
Kreisförmige Rechenscheibe mit einer logarithmischen Skala und sechs trigonometrischen Skalen (jeweils 2 Bereiche von Sinus und 3 Bereiche von Tangens) sowie einer Skala der dekadischen Logarithmen ►William Oughtred |

|
Instrumentum Mathematicum
Universale Johannes Matthes Biler Jena 1696 nach Jacob Leupolds "Theatrum Arithmetico-Geometricum" 1727 Reproduktion R.A. 2019 |
Rechenscheibe mit fünf halbkreisförmigen Skalen: 1. von innen (verstellbar) log Skala 1...10...100 2. (fest) log Skala 1...10...100 3. Winkel hier aufsuchen, Tangens auf Skala 2 4. Winkel hier aufsuchen, Sinus auf Skala 2 5. Gradskala 0° - 180° zum Messen und Zeichnen Als Läufer dient ein Bindfaden |

|
Palmer's Computing Scale 28x28 cm 65 cm-Skala Aaron Palmer George Fuller um 1845 Boston, USA Reproduktion R.A. 2018 |
Vorderseite: "Palmer's Computing Scale" Doppelskala mit
zahlreichen Markierungen für "Gauge Points" (Umrechnungsfaktoren),
insbesondere für amerikanische und englische Währung und
Zinsfaktoren Rückseite: "Fuller's Time Telegraph" zur Errechnung der Tage zwischen zwei Kalenderdaten in der Zinsrechnung ►sliderules.info ►sliderulemuseum |

|
Calculigraphe System Boucher Ø 6cm, 12 cm-Skala Frankreich 1876 Henri Chatelier Paris USA: $ 8,50 ►Anleitung |
Rechenuhr für allgemeine Anwendungen System Boucher: feste Marke auf Deckglas und beweglicher Zeiger (Knopf 1 dreht Skala unter fester Marke, Knopf 2 bzw. Knopf 1 mit Taste dreht Zeiger) Vorderseite: log Skala 1-10, dazu Quadratwurzel und Gradskal für Sinus Rückseite: Kubikwurzel und Logarithmus ►Geschichte1 ►Geschichte2 ►Katalog 1899 |

|
Calculimètre Ø 6cm, 16 cm-Skala Georges Charpentier Frankreich 1881 Tavernier-Gravet u.a. in USA vertrieben von Keuffel & Esser, Dietzgen ►Animation ►Animation2 Gebrauchsanweisung |
Rechenscheibe für allgemeine Anwendungen Doppelskala für Multiplikation und Division, außerdem Quadratwurzelskala. Rückseite: Zehnerlogarithmen für höhere Potenzen und Wurzeln, Sinusskala, Tangensskala ►mehr Info ►Rechenbeispiele ►Calculimètre-Selbstbau ►Patent ►Varianten1 ►Varianten2 |

|
Halden Calculex Ø 6,4cm, 16 cm-Skala Joseph Halden & Co. Ltd. Manchester patentiert 1905 1 £ 6s Anleitung |
Rechenscheibe für allgemeine Anwendungen Vorderseite von außen nach innen: Zehnerlogarithmus, log. Doppelskala für Multiplikation und Division, Quadratwurzelskala Rückseite von außen nach innen: Gradskala (für Sinus), log. Skala, reverse log Skala, Kubikwurzelskala ►Kritik |

|
Fowler's Calculator Type H Ø 2,5" 20 cm-Skala Fowler & Co, Manchester SN 5090 ab 1915 Preis 37s 6d |
Drehbare Skala unter fester Marke auf Deckglas und beweglichem
Zeiger (System Boucher) Vorderseite: log. Skala, Reversskala 1/x für Division, linerale Logarithmenskala, Wurzelskala in zwei Abschnitten, Sinusskala Rückseite: log. Skala und Kubikwurzelskala in drei Abschnitten ►Firmengeschichte ►Fowler Rechenuhren |

|
Krugowaja Logarifmitscheskaja Linejka KL-1 Ø 5 cm 10 cm-Einzelskala Berchne-Bolschtschskij Iwanowo, UdSSR ab ca. 1965 Preis: 3 Rubel 10 Kopeken Anleitung ►Vorführung |
Multiplikation, Division über drehbarer kreisförmige 11 cm-Skala
mit Marke und Zeiger, außerdem Quadrate und Quadratwurzeln. Rückseite: Sinus, Tangens auf feststehender Skala. Verknüpfung von Vorderseite und Rückseite über gekoppelte Zeiger. |
 |
Rechenscheibe Nr. 1 Ø 30 cm, 75 cm-Skala patentiert 1904 K.Emil Tröger, Mylau Dieses Exemplar ca. 1965 Hans Tröger Kirchenthumbach/Opf. |
Rechenscheibe großer Genauigkeit mit Läufer.
Multiplikation und Division über Doppelskala Teilung 0,005/0,01/0,02 Feste Markierungen für Pi, kW/PS u.a. Angeboten wurden auch eine gleich große Scheibe mit zusätzlicher Kehrwertskala, eine größere Scheibe (Ø 39 cm) und eine kleinere Scheibe Ø 15 cm ohne Läufer, Teilung 0,01/0,02/0,05 und Rechenscheibe für Grafiker |

|
Pythagoräische Rechenscheibe 14x15cm, 35 cm-Skala Entwurf 1883: Donatus Röther, Weiden Version von 1907 2 Mark im Selbstverlag, später Reiss, Liebenwerda ►Animation Anleitung |
Rechenscheibe speziell zur Landvermessung. Logarithmisch geteilte Skala mit fester Marke und beweglichem Zeiger für allgemeine Berechungen, dazu lineare Skala der Zehnerlogarithmen zur Berechnung von Potenzen und Wurzeln. Weitere Skalen: "t", "u", "tang", "cos aus tang" und "sec aus sinus" zur direkten Umrechnung von Seiten im rechtwinkligen Dreieck und "segm λ" zur Berechnung von Kreisabschnitten Näheres |

|
Pythagoras- und Rechenscheibe 24x24cm, 53-cm-Skala Dipl.-Ing. K. Gampert ca. 1920 Reproduktion R.A. 2019 ►Original ►Animation Kurzanleitung |
Log. Skala zur Multiplikation und Division mit fester Marke und Läufer Zwei gegeneinander verschiebbare Skalen. Außerdem zwei spiralförmige "Pythagoras-Skalen" zur Ermittlung der dritten zu zwei gegebenen Seiten im rechtwinkligen Dreieck. |

|
Circular Columbus Calculator Columbus Calculator Co Wien 1922 Ø 12,5 cm 35-cm-Skala Anleitung |
In Deutschland selten angebotene
Rechenscheibe mit zwei beweglichen Cursors. Log. Skalen für Multiplikation, Division, Quadrat- und Kubikwurzel Sinus und Tangens Außerdem lineare Logarithmenskala Auf der Rückseite befindet sich eine Tabelle mit spezifischen Gewichten und Konstanten. |
|
|
%-Calculator System H-C-Lange H.C.Lange, Elmshorn |
Kaufmännische Rechenscheibe zur Bestimmung prozentualer Zuschäge oder Abzüge auf Ein- und Verkaufspreise. Auch als universeller Rechenschieber verwendbar. |
 |
Rechenscheibe
8/10 Ø 12,5 cm, 26 cm-Skala Faber Castell ca. 1969 Anleitung |
Multiplikation und Division über Doppelskala mit Läufer. Spezielle Skalen für x², x³, sin, tan, arc. Kreisberechnung, Umrechnung kW <-> PS. |
|
ABC-Rechner IWA 1638 System Wern 21*21 cm 52-cm und 33-cm-Skala 1966 29 DM ►Animation ►Anleitung ►Patent Druckvorlage |
Rechenscheibe die im Bereich von 0,001 bis 1.000.000 außer der Ziffernfolge auch die Größenordnung der
Operatoren verarbeitet. Erstes Skalenpaar (51 cm, Fehler<1%) Zweites Skalenpaar (33-cm-Skala, Fehler<0,2%) Multiplikation, Division, Dreisatz und Proportionen, prozentuale Auf- und Abschläge, Umrechnung diverser Einheiten. Außerdem x², x³, sin, cos, tan in Grad und Rad, Potenzen, Wurzeln und Logarithmen im Bereich 1,001 bis 1040. ►Info ►Loblied ►Rechnerlexikon ►Youtube |

|
IWAMATIC 1660 Ø 11 cm 30 cm- und 21 cm-Skala IWA, Esslingen 1972 35 DM Gebrauchsanweisung ►Patent |
Rechenscheibe, bei der die beiden Operanden und das Ergebnis der Rechnung
untereinander abgelesen werden können. Erreicht wird dies durch ein
Planetengetriebe, dessen (fester) äußerer weißer Skalenring innen mit einem
Zahnkranz versehen ist. Der drehbare weiße innere Skalenring außen
verzahnt (Sonnenrad). Der mittlere graue Skalenring dreht sich über Planetenräder
gekoppelt mit halber Geschwindigkeit. Skalen von außen nach innen: Logarithmusskala, Skalen A, B invers, B, C invers, Sinus, Tangens. |

|
Circle Profit Calculator Ole Jorgensen ca. 1970 |
Stftebecher für den Schreibtisch mit Skalen auf der Ringaußenseite ("Rechenrad") Eine feste lineare Skala und vier verstellbare ringförmige logarithmische Skalenringe - Linearskala 0-100 - prozentuale Subtraktion - prozentualer Vergleich - prozentuale Addition - log. Skala von 1 bis 10 Auch als "Universal Circle Calculator" mit Quadratskala und Kubikskala statt Prozentskalen. |
|
Geräte mit langen Skalen: Die typische Gunter-Skala ist 24 Zoll lang und reicht über 2 Größenordnungen von 1 bis 100. Die Skala für eine Größenordnung war also mit 12 Zoll etwa so lang wie die 25 cm-Skala des im 20. Jahrhundert gebräuchlichen Rechenschiebers. Schon im 16. Jahrhundert bestand jedoch das Bedürfnis nach genaueren Skalen: Die kreisförmige Skala auf Oughtreds Rechenscheibe war etwa 76 cm lang. Bereits um 1660 entwickelte John Brown eine Rechenscheibe, deren spiralförmige Skala in fünf Windungen eine Länge von 2,13 m erreichte. Überdies war sie von innen nach außen geführt und verbesserte so die kritische Ablesegenauigkeit am Ende der Skala. Auch in den folgenden Jahrhunderten erschienen immer wieder neue Geräte. Auf Nystrom's Calculator von 1848 waren die Skalenabschnitte sägezahnförmig in die Breite geführt. Bei anderen Rechenscheiben und Rechenuhren war die Skala abschnittsweise (Fowler) oder spiralförmig (Atlas, Logomat) von innen nach außen geführt. Bei Rechenzylindern war sie schraubenfederförmig um einen Zylinder gewickelt (Fuller, Otis King). Hinzu kamen Rechentafeln und Rechenroste, deren Skalen in Abschnitte aufgeteilt und nebeneinandergelegt (Multiplex, Illgen, Logaritmal) und Rechenwalzen, bei denen die Abschnitte um einen Zylinder angeordnet waren (Thacher, Loga). ►Überblick von Ed Chamberlain ►Skalen |
||
 |
Faber-Castell 342
1923 Columbus Sys. Rohrberg zweigeteilte 50 cm-Skala Nestler No. 18 ab 1912 mit 50 cm-Skala Faber-Castell 1969 Novo-Duplex 2/83N mit Wurzelskala ►Animation ►Näheres ►Manual |
Schon früh gab es viele Modelle wahlweise außer mit 25 cm auch
mit 50
cm Länge (z.B. Nestler No.18).
Der Mathematiker Albert Rohrberg verlängerte 1923 das C- und D- Skalenpaar eines kaufmännischen Rechenstabs
auf 50 cm und teilte es in zwei Hälften. Die gegenüber dem Standard
leicht veränderte Handhabung erlaubte nun Rechnungen mit drei
Operanden (z.B. zur Berechnung von
Tageszinsen) mit nur einer Einstellung aber mit doppelter Genauigkeit. Einige späte Duplex-Stäbe von Faber-Castell ersetzten die A/B und die C/D-Skala durch eine doppelt so lange zweigeteilte "Wurzelskala", mit der man auch doppelt genau multiplizieren und dividieren konnte. |

|
Nystrom's Calculator John W. Nystrom 1848 Ø 24 cm Hersteller: George Thorsted New York ,USA Preis 1854 $20 Reproduktion R.A. 2020 ►Animation ►Anleitung ►Patent |
Messingscheibe mit logarithmischer Skala und Sinusskala für
Punktrechnung (3-4-stellig), lineare Skala (2-3-stellig) zur
Addition von Logarithmen, jeweils mit Sägezahnbögen zur genauen Ablesung von
Zwischenwerten. Außerdem ganz innen eine Kompassskala "Points" zur Navigation. Zwei Zeiger, die separat eingestellt und gegeneinander arretiert werden können. Merkscheibe zum Verfolgen der Größenordnung ►Patentmodell ►späteres Modell ►Druckvorlage1 Druckvorlage2 |
|
|
Fowler "Magnum" Long Scale Calculator Modell 4MTG1 Ø 4 5/8" 1,27 m-Skala (6 Abschnitte) Fowler & Co Manchester, UK ab 1927 Preis: 1£ 6s Anleitung |
Multiplikation und Division über drehbare Skala mit fester Marke auf
Deckglas und drehbarem Zeiger. Kreisförmige Skala ca. 33 cm mit zugehörigen Skalen für Wurzel, Reziprokwert, Logarithmus, Sinus und Tangens. Zusätzliche Langskala ca. 1,27 m, aufgeteilt auf sechs konzentrische Kreise, angeordnet von innen nach außen zur Verbesserung der Ablesegenauigkeit. Näheres ►Innenleben |
|
|
The Atlas Calculator Ø 21 cm spiralförmige 11,80 m-Skala Gilson Slide Rule Co. Stuart Florida 1931 ►Anleitung |
Multiplikation und Division mit zwei Zeigern über einer
kreisförmigen und einer spiralförmigen Skala. Außen befindet sich die kreisförmige Skala für etwa vierstellige Genauigkeit. Bei Bedarf erfolgt eine Feinkalkulation auf der Spiralskala mit 30 Windungen. Die Rückseite enthält trigonometrische Skalen (Sinus, Cosinus, Tangens) und dezimale Äquivalente für Brüche bis 1/64. ►Entwicklung |
|
Tyler Slide rule 21,5x21,5 cm Logarithmische Spirale ca. 33 cm John Tyler Weems, Annapolis, USA ca. 1955 Reproduktion R.A. 2020 ►Animation |
Sehr unkonventionelle Rechenscheibe Logarithmische Skala in Form einer log. Spirale Ein fester Index und ein beweglicher Läufer für Proportionen, Multiplikation und Division Funktionsgraphen für Quadratwurzel, Sinus/Cosinus, Tangens und nat. Logarithmus Lineare Randskala für Zehnerlogarithmus Näheres ►Photocalcul |

|
Logomat Pfiffikus 2001 Ø 4,5 cm spiralförmige 35 cm-Skala (!) Logomat Rechengeräte Pfungstadt ca. 1971 Einzelpreis 5 DM Anleitung |
Multiplikation und Division mit zwei Zeigern über Spiralskala mit 3
Windungen, angeordnet von innen nach außen zur Verbesserung der
Ablesegenauigkeit. Einige Geräte doppelseitig mit Quadrat- und Kubikskala auf der Rückseite. Gerät, Etui und Anleitung in Streichholzbriefchengröße |
|
|
Logomat mini 2000 Ø 9 cm spiralförmige 60 cm-Skala Logomat Rechengeräte, Pfungstadt ca. 1972 34,80 DM Anleitung |
Universelle Rechenscheibe für Multiplikation und Division auf Spiralskala
mit drei Windungen. Ein Lupenläufer steigert die Ablesegenauigkeit. Zusätzlich austauschbare "Programmscheiben" als anwenungsspezifische Rechenhilfe für - fremde Währungen - Maße und Gewichte - prozentuale Aufschläge und Rabatte - Kehrwert - zweite und dritte Potenz und Wurzel |

|
Double Logarithmic Decadic Long-Scale Calculator Oliver Steffens Neuentwicklung 2020 |
Drehbare Scheibe mit festem Index und extrem genau ablesbarem
verstellbarem Nonius-Läufer. Kreisförmige Skala y ca. 30 cm lang, dazu die Skalen 1/y, y², sin(y), tan(y). Auperdem die "Pythagorasskala" √(1- 0,1y²) und die Logarithmenskala. Spiralförmige logarithmische Skala über drei Windungen, verwendbar für Kubikwurzeln, mit von innen nach außen wachsender Genauigkeit und zwei begleitende Log-Log-Skalen 10x und 10x/10 für beliebige Potenzen und Wurzeln. |

|
Fuller's Calculator Stanley, London 12,7 m-Skala (500 Zoll in 50 Spiralwindungen) Modell 1, ab 1877 (dieses Exemplar 1930) SN 6291 30 Preis 1913: 30$ Preis 1938: 5£ 10s Anleitung Anleitung Barnard Simulation zum Download |
Beim Fuller-Rechenzylinder ist eine 12,7 Meter lange Skala
spiralfederförmig um einen Zylinder gewickelt. Das erlaubt Multiplikation und Division mit zwei Zeigern über einzelner Skala. Bis zu fünfstellige Genauigkeit. Logarithmen können auf über kleineren Hilfsskalen abgelesen werden, dadurch ist die Berechnung von Potenzen und Wurzeln möglich. Auf dem mittleren Zylinder Hilfstabellen für Sinus und Dezimalteile von englischen Maßen, bei Modell 2: Hilfstabellen für sin und log. |

|
Rechenzylinder für komplexe Zahlen nach D.J. Whythe Stanley London 1962 1) Nachbau R.A. 2017 aus Teilen eines Fuller Calculators 2) Nachbau R.A. 2015 nach ►Bauanleitung von Robert Dawson |
Exkurs:
Im Jahre 1962 kam der "Stanley Complex Number Slide Rule" auf den
Markt, eine Variante von Fuller's
Calculator, mit der man
die Multiplikation komplexer Zahlen (2+5i) * (3+7i)
grafisch durchführen konnte, ohne Teilprodukte ausmultiplizieren und
addieren zu müssen. Anwendungsbeispiel ►The Whythe Complex Slide rule in Fuller Style ►Wikipedia ►Calculating History ►Tina's Complex Number slide Rule ►Rechnen mit komplexen Zahlen |

|
Otis King's Calculator
Carbic Ltd., England ab 1921 1,70 m-Skala oben: Modell K, SN V6874 1962, 3£ unten: Modell L, Nachbau R.A. 2005 |
Der deutlich handlichere Otis King besitzt ebenfalls eine
Spiralfeder-Skala und erlaubt
Multiplikation und Division übert zwei Skalen und Läufer mit etwa vierstelliger Genauigkeit. Modell K mit doppelt ausgeführter Skala auf dem inneren Zylinder (spart Einstellbewegungen), Modell L mit zwei einfachen log. Skalen und zusätzlicher linearer Mantissenskala zur Bestimmung von Wurzeln und Potenzen. ►Näheres bei Dick Lyon |

|
Thacher's Calculating Instrument Keuffel & Esser, New York 9,10 m-Skala ab 1881 (dieses Exemplar 1927) SN 5289 Preis 1913: 35 $ Kurzanleitung |
Anders arbeitet ie Rechenwalze von Ewin Thacher. Hier sind die
Skalen in parallel angeordnete Abschnitte aufgeteilt.
Multiplikation und Division erfolgen auf den gegeneinander verschiebbaren teilweise
überlappenden Skalenabschnitten mit bis zu fünfstelliger Genauigkeit. Die Innenskala trägt 20 parallele Abschnitten auf einem Zylinder (60 cm lang Ø ca. 10 cm). Die Gegenskala ist auf einer Hülle aus 20 dreieckigen Gitterstäben aufgetragen, dort finden sich außerdem zusätzliche Skala für Quadrate, Quadrat- und Kubikwurzeln. Näheres Skalenbild |

|
Loga Calculator 10 RD Heinrich Daemen-Schmid Uster-Zürich, Schweiz 10 m-Skala (Deckelbeschriftung 15m) SN 10 9366 erstmals patentiert 1907 dieses Exemplar etwa 1930 Preis 1921 500 Fr ►Anleitung ►Patent |
Hier trägt die verschiebbare Manschette eine 10 m-Skala (50 parallele Abschnitte von 21 cm
Länge) und der darunterliegende weiße Zylinder (Ø 16 cm Länge 45 cm)
50 überlappende Abschnitte mit doppeltter Länge. Die Log. Skala
ermöglicht mit vier-
bis fünfstellige
Genauigkeit. Auf der Manschette sind Reziprokwerte (grün) und Kreisdurchmesser (rot) entsprechend der schwarz markierten Skalenwerte eingetragen. Das Gerät besitzt Bremsen, um Manschette zu fixieren, und aufsteckbare Reiter für Konstanten (z.B. Wechselkurse) Spätere Rechenwalzen ►Modell- und Preisliste ►Rechnerlexikon |
|
|
Illgen'sche Rechentafel 2 m - Skala, vierfach Paul Illgen, Leipzig Preis ca. 1920: 60 M |
Das gleiche Konstruktionsprinzip wie bei der Loga wurde hier in die
Ebene ausgebreitet. Die
Multiplikation und Division (besser: Dreisatz und Proportionen)
erfolgt über
ein Rechengitter mit Doppelskala in zehn Abschnitten auf einer durchsichtigen "Glimmer"-Platte.
Die vier Mal so große Grundplatte aus Blech erspart das "Durchschieben". Gebrauchsanweisung und Reklameblatt. ►Ähnlich: Calculigraph |
|
|
Graphische Rechentafel aus: "Der Multiplex" von Friedrich Schneider 50 cm-Skala München 1909 (Nachbau nach Buchillustration) Druckvorlage |
Eine ähnliche Konstruktion in Billigausführung. Multiplikation, Division mit Rechengitter 21,5x13,5 cm mit Doppelskala in zehn teilweise überlappenden Abschnitten. Außerdem Proportionen, Quadrat- und Kubikwurzel mit 3- bis 4-stelliger Genauigkeit. Näheres |

|
Logaritmal 1,5 m-Skala Ing. Dr. Vaclav Jelinek Buchhandlung Peroult, Mährisch Ostrau Tschechische Republik Preis 1943: 6,60 RM Animiertes Modell (mit vierfacher Grundplatte) Simulation zum Download Druckvorlage mit Anleitung |
Und hier die die postkartengroße Kleinausgabe.
Multiplikation und Division über Rechengitter mit Doppelskala in jeweils
zehn Abschnitten. Zusätzliche Skala zur Bestimmung von Zehnerlogarithmen zwecks Berechnung von Potenzen und Wurzeln. |

|
Universal Calculator Graphische Logaritmentafel Columbus Calculator Co. (Buchbinder Franz Kritz) Wien ca. 1920 |
Klapptafel mit
einer 3 m langen Doppelskala in 20 Abschnitten. Eine lineare Skala
von 0 bis 100 (Ziffern schwarz) ist kombiniert mit einer
logarithmischen Skala von 100 bis 1000 (Ziffern rot). Man sucht auf
der roten Skala zwei Zahlen auf und liest daneben auf der schwarzen
Skala deren Logarithmus ab. Diese addiert man mit dem
Zahlenschieber, sucht auf der schwarzen Skala die Summe auf und
liest auf der roten Skala das Produkt ab. ►Columbus
Addiergerät ►Maximator-Tabelle |
|
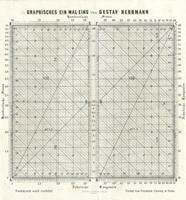
Das graphische 1x1 oder die Rechentafel, ein Ersatz für den Rechenschieber Gustav Herrmann Vieweg Braunschweig 1875 Anleitung Rechentafel besser aufgelöst |
Ausführung von Multiplikation, Division, Potenzieren und Radizieren
mit
beliebigen auch gebrochenen Potenzen durch Verfolgen von Linien in einem
quadratischen Raster mit logarithmischen Randskalen. Dazu
Randskalen in Grad, um mit trigonometrischen Werten
arbeiten zu können. Zwei Jahre später erschien mit "Herrmanns Rechenknecht" eine aufwendige Rechenscheibe mit 10 konzentrisch angeordneten Skalen und eine zweite Ausführung mit Fünfmeterskala. |
|
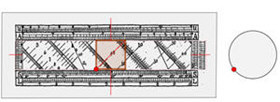
Rechendreher nach Dr. Philipp Lötzbeyer Neukölln 1923 DRP 383821 Nachbau R.A. 2021 ►Animation ►Patentschrift |
Alternativentwurf
für universelle Rechenschieber. Multiplikation und Division auch mit Sinus- und Tangens-, Kehrwert-, Quadrat- und Kubikskala, lineare Logarithmusskala. Die Operanden werden auf zwei üblichen log. Skalen eingegeben, die jedoch paarweise um 90° gedreht angeordnet sind. Abgelesen wird das Ergebnis auf einem um 45° gedrehten zweidimensionalen Nomogramm, das mittels Drehknopf unter einem Fenster verschoben werden kann. Details |
Rechenwerkzeug.de