Ein Rechenstab für komplexe Zahlen
 Worum geht's?
Worum geht's?
Die Gleichung x² - 6x + 13 = 0 ist in der Menge der reellen Zahlen nicht
lösbar.
Nach der bekannten p/q-Formel erhält man die Lösungen
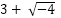 und
und 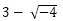 .
.
Wurzeln aus negativen Zahlen sind in der Menge der rellen Zahlen nicht
definiert. Um trotzdem mit ihnen rechnen zu können, klammert man aus der
Wurzel alles außer -1 aus und schreibt die Wurzel aus -1 kurz als i : 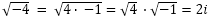 .
.
Die Lösungen der
genannten Gleichung kann man dann kurz als 3+2i und 3-2i
schreiben. Einen solchen Ausdruck nennt man eine komplexe Zahl. Sie besteht
aus dem Realteil 3 und dem Imaginärteil 2i. In vielen Fällen verschwindet im
Laufe weiterer Berechnungen der Imaginärteil wieder, und man erhält für das eigentlich
gestellte Problem zuletzt ein reelles
Zahlenergebnis.
Die Zwischenschritte weiterer Rechnungen sind aber von dem Moment an, wo komplexe Zahlen ins Spiel kommen, recht mühsam. Jede Multiplikation von zwei komplexen Zahlen verlangt vier Multiplikationen und zwei Additionen ...
(3+2i) * (5+3i)
= 3*5 + 3*3i + 2i*5 + 2i*3i
= 15 + 9i + 10i -
6
(da: 2i*3i = 2*3*i*i =6i² = -6).
= 9 + 19i
... und die Division ist noch viel aufwendiger. Dieser Aufwand schreit nach einem Hilfsmittel. 1962, ein paar Jahre vor der allgemeinen Verfügbarkeit von Computertechnik, war "Stanleys Complex Number Slide Rule", entworfen von D.J. Whythe ein professionelles Werkzeug für solche Berechnungen.

Die Skala
a)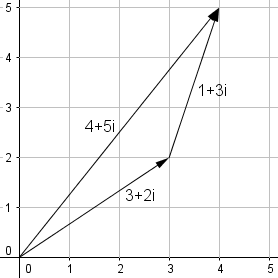 b)
b) 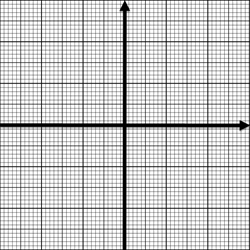 c)
c) 
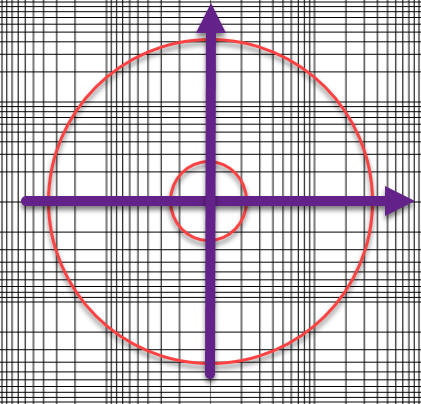
Komplexe Zahlen können als Zeiger in einer Zahlenebene dargestellt werden. (Abb. a) Entlang der horizontalen Achse wird dabei der reelle, entlang der vertikalen Achse der imaginäre Teil abgetragen. Zur Verkettung zweier Zeiger werden die beiden Komponenten getrennt addiert. Auch Whythe verwendet bei seinem Rechenzylinder die Darstellung in einer Zahlenebene. Allerdings sind die Achsen, weil hier nicht addiert, sondern multipliziert wird, nicht linear (Abb. b), sondern logarithmisch skaliert (Abb c).
Aber warum sind die Gitternetzlinien gekrümmt? Um das Koordinatensystem um einen Zylinder wickeln zu können, hat Whythe aus der Zahlenebene einen Kreisring mit einer logarithmischen Dekade von 1 bis 10 ausgeschnitten. Diesen Ring hat er dann innen gedehnt und außen gestaucht, sodass beide Kreise den gleichen Radius bekamen. Die vorher geraden Gitternetzlinien nehmen dabei die Form eines U an und die vier Halbachsen liegen nun parallel nebeneinander. Aber die geometrische Operation des Aneinanderleges von Zeigern funktioniert nach wie vor. Nur liefert die Addition zweier Zeiger auf der logarithmischen Skala nicht die Summe, sondern das Produkt der Operanden.
Hier der aufgeschnittene Zylindermantel als Rechteck:
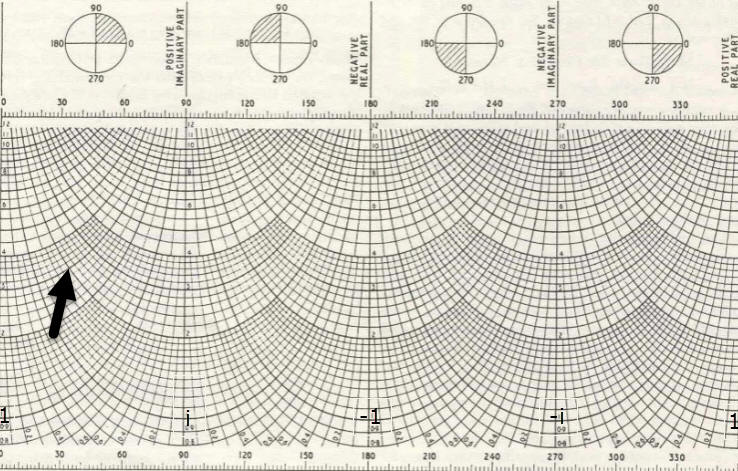
Am unteren Rand der Skala sind also von links nach rechts vier Markierungen sichtbar: Die 1 der realen Komponente, das i der imaginären Komponente, die -1 der realen Komponente und das - i der imaginären Komponente. Um einen Zylinder herum angeordnet ist die rechte Seite des Rechtecks mit der linken zu einer Endlosskala verbunden.
Man findet eine komplexe Zahl dort, wo die Kurve ihres reellen Teils die Kurve ihres irrealen Teils schneidet. Um die komplexe Zahl 3+2i aufzusuchen, geht man also von der 1 aufwärts zur 3 und vom i aufwärts zur 2i Von der 3 aus verfolgt man die schwarze Kurve nach rechts, von 2i aus die rote Kurve nach links. Dort, wo sich beide Kurven schneiden (Pfeil), ist der Ort von 3+2i. Die Zahl 3-2i findet man, indem man von der 3 nach links und von -2i nach rechts geht. (Zur Erinnerung: Der rechte Rand klebt am linken!)
Der Rechner von Whythe benötigt nur eine logarithmische Skalendekade (1..10), da seine Cursors transparent sind. Der kurze, fest mit dem Griff verbundene Cursor trägt eine Markierung an der Spitze. Der doppelt so lange, über der Skala bewegliche Cursor jedoch besitzt eine zweite Markierung, die gegenüber der Spitze um eine Skalenlänge verschoben ist. In den Fällen, wo die eine Cursormarkierung bei einer Rechnung unten aus der Skala hinauswandert, tritt eine zweite, um eine Skalenlänge verschobene Cursormarkierung von oben in die Skala ein.
Das Gerät
Ich habe den Whythe-Rechner zweimal rekonstruiert. Zuerst nach einer Bauanleitung von Robert J MacG Dawson.
Meine Variante besteht aus
• der Rollenverpackung eines
Posters,
• einer ausrangierten Gardinenstange,
• einer schmalen
Holzleiste und
• der von Robert Dawson konstruierten Skala, die man
hier herunterladen kann.
Die Skala von Robert Dawson ist gegenüber der originalen Skala von Whythe nach oben verdoppelt. Dies ist erforderlich, da die Variante von Dawson für zwei hölzerne Cursors ausgelegt ist, die beide nur an der Spitze abgelesen werden können. In der Abbildung ist der untere der feste Cursor und der obere der bewegliche Cursor. Insgesamt ist der Dawson-Rechener mit der zweifarbigen und verdoppelten Skala erheblich besser abzulesen als das Original von Whythe.
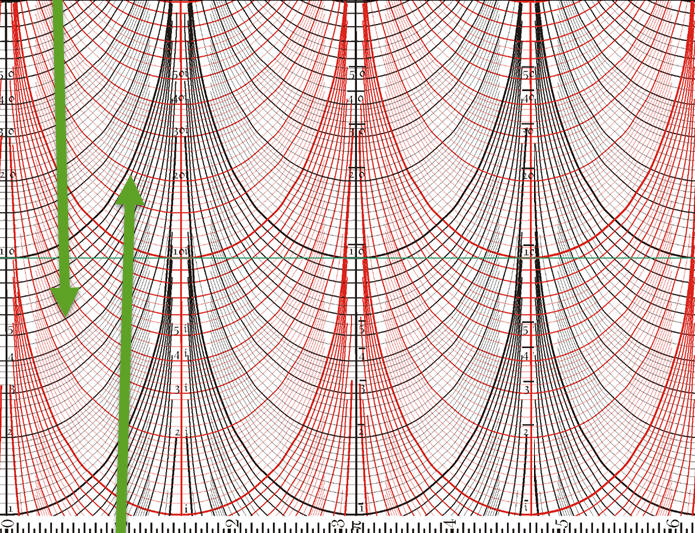
Multiplikation
Man bewegt den Zylinder so, dass der feste Cursor auf den ersten Faktor (3+2i) zeigt. Dann stellt man den beweglichen Cursor so ein, dass er auf die 1 zeigt (1+0i). Anschließend bewegt man den Zylinder so, dass die Spitze des beweglichen Cursors auf den zweiten Faktor (5+3i) zeigt. Der feste Cursor zeigt nun - siehe Abbildung - auf das Produkt (9+19i) und kann direkt als Faktor oder Dividend einer Folgerechnung verwendet werden.
Division
Man bewegt den Zylinder so, dass der feste Cursor auf den Dividenden zeigt, dann den beweglichen Cursor so, dass er auf den Divisor zeigt. Anschließend bewegt man den Zylinder so, dass der bewegliche Cursor auf die 1 zeigt. Der feste Cursor zeigt dann auf den Quotienten.
Später habe ich die Zylinder eines heruntergekommenen Fuller Calculators mit einer auf Fotopapier ausgedruckten Skala aus dem Journal of the Oughtred Society und zwei auf Plexiglas selbst gemalten Skalen versehen und so eine ziemlich originale Kopie des ursprünglichen Modells von Whythe erhalten.

Näheres: D.J. Whythe, "The Whythe Complex Slide Rule In Fuller Style",
Journal of the Oughtred Society 8(1) (1999) p.15
Rechenwerkzeug.de