Die pythagoräische Rechenscheibe von Röther
Ein Fundstück als Forschungsauftrag
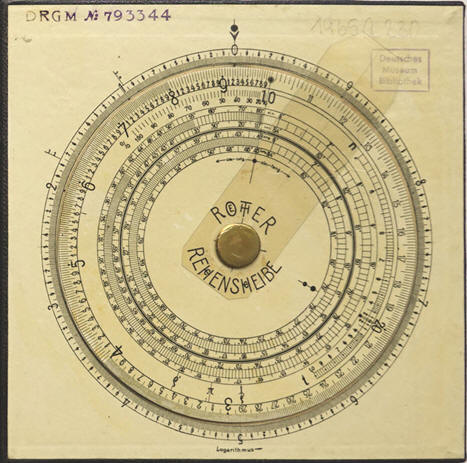
Rechenscheibe im Layout von 1899 (Gradskala auf der Grundplatte hinzugefügt)
Röther?_Nie_gehört!
Das kann_ich_besser!
Präzisionsinstrument_aus_der_Bastlerwerkstatt
Skalenstriche_positionieren_-_eine_Sträflingsarbeit
Exakt_-_aber_preiswert
Scheiben_für_Haus-_und_Feldgebrauch
Was heißt hier "pythagoräisch"?
Zwei_Werkzeuge_im_Vergleich
Wie wär's mit_einer_Rechenmaschine?
Modellpflege_posthum
Epilog
Als ich vor einiger Zeit nach einem kürzlich erschienenen Buch recherchierte, fiel mir zusätzlich eine antiquarisch angebotzene Rechenscheibe ins Auge - durch ungewohnte Skalen, vergilbtes Papier und ihre grafisch ansprechende Jugendstil-Beschriftung. Das "Buch" bestand aus zwei stoffüberzogenen Platten aus Hartpappe, einer dünnen, drehbaren Skalenscheibe, einem durchsichtigen Zelluloidstreifen mit eingeritzter Haarlinie als Läufer und einer Reißzwecke als Achse. Die Gebrauchsaweisung fehlte. Da der Preis überschaubar war, kaufte ich das merkwürdige Objekt. Und schon bevor die Lieferung eintraf, begann ich ein wenig zu forschen.
Auf der Suche nach einschlägigen Informationen stieß ich auf einen Geometer, der in den Jahren 1877 bis 1879 als Vermesser und Kartierer am Kataster von Nürnberg mitgewirkt hatte, 1882 die Stelle als Bezirksgeometer in Weiden übernommen hatte und 1883 als Mitglied in den Historischen Verein der Oberpfalz aufgenommen wurde.
Donat Röther (auch Donatus Roether) wurde am 27. März 1851 in Kissingen geboren. Dort war schon sein Vater Michael Röther Bezirksgeometer für den Bezirk Münnerstadt gewesen. Donat besuchte die königliche Studien-Anstalt Münnerstadt und das königliche Realgymnasium Würzburg. Seine Noten waren eher unterdurchschnittlich: Im Schuljahr 1866/67 erreichte er einen Notendurchschnitt von 3 und lag auf Platz 10 von 12 Schülern der Klasse, nur im Zeichnen hatte er eine 1. Nach dem Militärdienst wurde er 1873 durch König Ludwig II von Bayern zum "Reserve-Second-Lieutenant" befördert. 1876 wohnte er in Nürnberg, 1878 in München. Laut dem Melderegister von Weiden i. d. Opf. erstattete er zehn Jahre später dort "Aufenthaltsanzeige". Er war verheiratet mit Margaret(h)a, geborene Seebauer, * 25. August 1854 in Nürnberg. Das Ehepaar hatte zwei Kinder, Eleonore, * 17. Juli 1878 und Julie/Julia, * 11. Juni 1881. Beide wurden in München geboren. Julie ist offenbar früh verstorben und in Kissingen beigesetzt. 1914 verzog die Familie Röther von Weiden nach Würzburg, wo er bereits seit 1903 als Bezirksgeometer amtierte.
In den "Heften zur Bayerischen Geschichte und Kultur Band 26: Wie Bayern vermessen wurde" erfuhr ich: "Geometer" ist eine allgemeine Bezeichnung für die bei der topografischen Landesaufnahme und beim Kataster tätigen Vermesser. Bayern wurde seit dem Beginn des 19. Jahrhunderts systematisch vermessen und der Bezirksgeometer war in seinem Bezirk für die Fortführung der Katasterkarten zuständig. "Erfahrene Geometer der Landesvermessung konnten sich für dieses Amt bewerben. Das Einkommen aus dieser verantwortungsvollen Tätigkeit, für die nur ein geringes Grundgehalt bezahlt wurde, war so bescheiden, dass nur wenige sich dafür interessierten. Die Aufsicht über die Bezirksgeometer oblag Kreisgeometern, deren Entlohnung offensichtlich nicht viel besser war." (S.53) "Die Geometer, ab 1828 auch die Obergeometer, waren nicht fest angestellt, sondern wurden für die abgelieferte Arbeit bezahlt. Auch die Instrumente waren auf eigene Kosten zu beschaffen. ... Erst ab 1878 gab es auch fest angestellte Geometer. Trotzdem lebten die meisten weiterhin von Akkordarbeit und Tagegeld. Im Jahr 1884 wurde dann der lange geforderte Gebührentarif eingeführt. Doch trotz all dieser Verbesserungen blieben die Geometer in den Augen der bürgerlichen Handwerksmeister 'arme Fretter' und 'Hungerleider'." (S.46)
Im Jahre 1887, als Bezirksgeometer von Weiden, hatte Donat Röther die Hungerleiderphase wohl hinter sich. Nicht ohne Stolz teilte er im Märzheft der "Zeitschrift für Vermessungswesen" (S. 302) mit, dass er seit vier Jahren mit einer selbst gefertigte Rechenscheibe arbeite und dass diese sogar genauere Ergebnisse liefere als andere auf dem Markt bereits eingeführte Geräte:
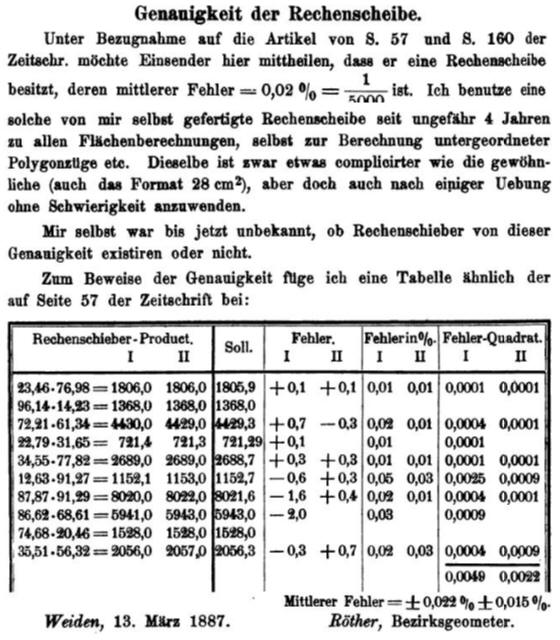
Wenn die 28 cm² kein Druckfehler sind, war Röthers erste Scheibe kaum größer als ein Logomat Pfiffikus. Der Rechenschieber, auf dessen Produktvorstellung auf Seite 57 in einem früheren Heft desselben Jahrgangs Bezug genommen wird, war der gerade neu erschienene zelluloidbeschichtete Stab von Dennert und Pape. Er hatte im Test eine maximale Abweichung von 0,16% geliefert.
In England waren logarithmische Rechengeräte nach der Erfindung der Gunterskala im Jahr 1620 kontinuierlich weiterentwickelt worden. Rechenschieber zählten bereits um 1800 zur Standardausstattung etwa von Seeleuten, Maschinenbauern und Steuerbeamten. Auch in Frankreich gehörte der Umgang mit Rechenschiebern (System Mannheim 1850) zum Anforderungsprofil höherer Beamter. In den USA wurden Rechenscheiben (Palmer's Computing Scale 1845) und bereits auch eine Rechenwalze (Thacher 1881) allmählich populär. In Deutschland dagegen waren trotz der frühen Veröffentlichungen von Michael Scheffelt (1708) und Jacob Leupold (1729) logarithmische Rechengeräte auch gegen Ende des 19. Jahrhunderts noch kaum verbreitet. Dennert & Pape (Aristo) produzierte 1872 den ersten Rechenstab in Serie, Nestler folgte 1878 und A.W. Faber 1892.
Röther, der um 1883 eine Rechenscheibe für seinen Dienstgebrauch entworfen hatte, war also damit in Deutschland eine Art Pionier.
Schon das Grundkonzept seines Geräts war eigenwillig. Nachdem 1632 bei Oughtreds "Circles of Proportion", der allerersten logarithmischen Rechenscheibe, eine Art Zirkel aus zwei Zeigern über einer einzelnen kreisförmigen logarithmischen Skala gedreht worden war, besaßen spätere Entwürfe analog zum Rechenschieber in der Regel zwei gegeneinander verschiebbare Skalen. Erst 1876 war mit dem Boucher Calculator ein dritter Typ patentiert worden: eine "Rechenuhr" mit einer festen Markierung in 12-Uhr-Position auf dem Deckglas und darunter einem drehbaren transparenten Läufer über einer ebenfalls drehbaren Skala. Röther war wohl der Erste und vielleicht auch der Einzige, der diese Anordnung auf eine Rechenscheibe mit fester Grundplatte übertrug. Die Mehrzahl der Anwender benutzte Geräte mit doppelter Skala. Für sie war die Arbeit mit Röthers Scheibe "etwas complicirter", sprich gewöhnungsbedürftig.
Präzisionsinstrument aus der Bastlerwerkstatt
Mein Exemplar des Geräts (d=11cm, A=95 cm²) ist eine merkwürdige Mischung aus Präzision und Bastelarbeit: Die eigentliche Skalenscheibe ist filigran und hochpräzise von Hand entworfen, jedoch einfach aus starkem Papier hergestellt. Man braucht die Fingernägel, um die Scheibe am Rand anheben und drehen zu können. Das dünne Läuferscheibchen und die Reißzwecke als Achse wirken alles andere als professionell, aber das Layout der Scheibe und die Vertiefung für den Reißnagelkopf im Deckel sind originelle Design-Ideen.
Vermutlich hätten sich weder Dennert noch Faber mit Papierscheiben an die Öffentlichkeit getraut. Der Standard waren immer noch Geräte aus Buchsbaum, mit eingeritzten Skalen und eingeschlagenen Ziffern. Dieter von Jezierski zitiert in "Rechenschieber - eine Dokumentation" einen Hinweis des englischen Herstellers Rabone, dass dort die Gunterlinie, also eine Skala mit 540 Teilstrichen von einem erfahrenen Handwerker in 10 Minuten in Buchsbaum eingeschnitten wurde. Dies geschah Strich für Strich auf jedem einzelnen Rechenstab mithilfe einer nicht näher beschriebenen Vorrichtung. Der französische Instrumentenbauer Paul-Étiénne Lenoir entwickelte jedoch schon um 1830 eine leistungsfähige Maschine, die gleichzeitig die Skalen von 8 Rechenschiebern gravieren konnte.

Die 1878 bzw 1891 patentierten Rechenwalzen von Thacher und Fuller besitzen Skalen auf bedrucktem und klar lackiertem Papier, aufgezogen auf eine feste Unterlage. Das 1892 erschienene erste Rechenschiebermodell von A.W. Faber ist aus Buchsbaum hergestellt die Skalen sind aber bereits aufgedruckt. Und 1886 begannen Dennert & Pape, die Oberfläche ihrer Rechenschieber mit weißem Zelluloid zu überziehen. Das manuelle Einritzen von Skalen in Buchsbaumkörper Geschichte. Die Ziffern scheinen dagegen auf maschinell gravierten Modellen noch lange von Hand positioniert und eingeschlagen worden zu sein.

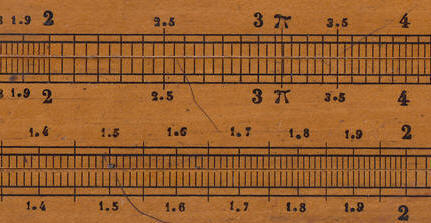
Tavernier-Gravet (Lenoir)
A.W. Faber
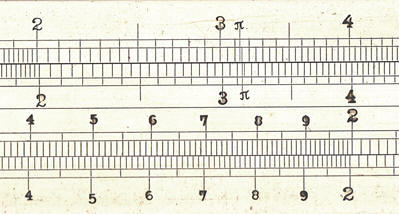
Dennert & Pape
Nestler (Billigmodell)
Röthers Scheibe fühlt sich an wie Baryt-Fotopapier. Während gedruckte Skalenstriche in der Vergrößerung leicht ausgefranst aussehen, sind Röthers Striche und Zahlen auch unter der Lupe scharf und sie zeigen minimale typographische Unregelmäßigkeiten. Ich vermute, dass Röther den Entwurf seiner Rechenscheibe im Großformat mit Tusche und Schriftschablonen auf einem Zeichenbrett erstellt hat, ihn dann abfotografiert und das Glasnegativ für jedes einzelne Exemplar der Scheibe auf Fotopapier kopiert hat. Verschiedene Ausgabeformate in kleinen Serien sind mit fotografischer Reproduktion leichter machbar als mit Drucktechnik. Auch damit beschritt Röther eigene Wege, und er nutzte dazu den damals aktuellen Stand der Fototechnik. Vor allem aber konnte er die selbe Vorlage in verschiedenen Größen reproduzieren, und er vermied dabei die Fehler, die beim manuellen Kopieren der Skala unvermeidlich auftreten.

Skalenstriche positionieren - eine Sträflingsarbeit
|
Nach seiner Mitteilung in der ZfV hat Röther seine Rechenscheibe „selbst gefertigt“. Was bedeutet das? Wie die Handwerker in England hat Röther die Skalenstriche auf seiner Druckvorlage wohl anhand von Funktionstabellen gesetzt. Bei der der Hauptskala konnte dabei er auf vorliegende Logarithmentafeln zurückgreifen, andere Skalen basieren auf Röthers eigenen Rechnungen.
Um Strecken
exakt zu teilen, hatte er sich ein Hilfsmittel konstruiert. Im
Katalog mathematischer und mathematisch-physikalischer Modelle,
Apparate und Instrumente (Nachtrag 1893 S. 39f) wird das
Instrument angeboten. Man kann damit Skalenstriche auf 0,1
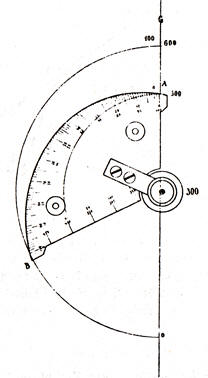
Millimeter genau setzen: "Polar- und Einteilungs-Masstäbe, construirt von Bezirksgeometer Röther in Weiden, ausgeführt und ausgestellt vom math.-mechanischen Institut von A. Ott in Kempten (Bayern.)
Diese Masstäbe beruhen auf der Eigenschaft der logarithmischen
Spirale, die darin besteht, dass zu gleichen Bögen gleiche
Differenzen der Radien nach den Endpunkten gehören. Bei dem
Polarmasstab ... ist die Curve aus einer Metallplatte
hergestellt und der Curvenrand in Millimeter geteilt, wobei die
Constante der logarithmischen Spirale so gewählt wurde, dass die
Radiendifferenz von einem Teilstrich bis zum nächsten 0,2 mm
beträgt. Mit Hilfe dieser Teilung können dadurch, dass man das
Instrument mit dem Pol auf eine Gerade legt und um denselben dreht,
auf dieser Geraden beliebige Längen
bis auf
1/10 mm
genau
abgetragen oder abgemessen werden.
|
 |
Im Jahre 1899, also zwölf Jahre nach der ersten Veröffentlichung, war Röthers Rechenscheibe so weit gediehen (siehe Abbildung ganz oben), dass er sie als Gebrauchsmuster 137583 schützen ließ und über die "Zeitschrift für Vermessungswesen" zum Kauf anbot. Nicht ohne Stolz berichtet er von erheblich gesteigerter Genauigkeit.

Er hatte den Durchmesser der Scheibe vergrößert, die Skala verlängert. Außerdem experimentierte er mit weiteren Skalen.

Mit dem Preis sprach Röther auch Kleinverdiener an. "Richtige" Rechenstäbe waren damals erst ab zehn Mark zu haben. Bestrebungen, Rechenstäbe im deutschen Schulunterricht einzuführen, stießen deshalb damals auf Widerstand: sie seien zu teuer (Ramm-Ernst: Stahlgehirne S. 34, Fußnote 69). Ob der Hinweis "Selbstverlag" bedeutet, dass er die Scheiben auch eigenhändig produziert hat? Zu Anfang wohl schon.
Bereits ein Jahr nach der Markteinführung meldete die "Zeitschrift für Instrumentenkunde" (S. 336): "Die kleine Röthersche Rechenscheibe erfreut sich bereits ziemlich großer Verbreitung." Die von Röther angekündigte genauerere Scheibe beurteilt der Rezensent wegen ihrer umständlichen Bedienung eher skeptisch.
Scheiben für Haus- und Feldgebrauch
Im Jahr 1907 - Röther war immer noch Bezirksgeometer, aber seit 1904 zuständig für Würzburg Stadt, Würzburg Land, Ochsenfurt und Röttingen - wurde eine weiter verbesserte Ausführung angekündigt Dafür erwirkte er einen neuen Gebrauchsmusterschutz DRGM 297600. Schon vorher hatte er mit dem "Optischen Institut Edmund Biow" in Würzburg einen Vertriebspartner und vielleicht auch Hersteller gewonnen. Googelt man Bilder von Röthers Rechenscheibe, so entdeckt man auch Ausführungen, die mit der Prägung "Reiss GmbH Liebenwerda" gekennzeichnet sind. Damit fand das Gerät schließlich einen in Fachkreisen renommierten Anbieter und bekam sogar einen Eintrag im Standardwerk "A History of the Logarithmic Slide Rule" (S. 95, Nr. 151) von Florian Cajori.
Mittlerweile gab es vier Versionen. Angeboten wurden: eine "Präzisionsrechenscheibe" d=22 cm, eine "Scheibe für den Hausgebrauch" d=18 cm, eine "für den Feldgebrauch" d=11 cm und eine Variante "im Taschenformat für gelegentliche Berechnungen" d=7 cm. Die beiden letzten sind "durch besondere Vorrichtungen vor Verletzungen geschützt".
Die "Präzisionsrechenscheibe" ist die oben rezensierte Version mit der abschnittsweise geteilten Skala. Eine Abbildung dieser Variante konnte ich bisher leider nirgends finden, sie war wohl ähnlich aufgebaut wie spater die Fowler Longscale Rechenuhren. Mitgeliefert wurde bei allen Scheiben das Heft "Rechenscheibe: Beschreibung und Anleitung zum Gebrauch derselben", verfasst von Erfinder höchstselbst und gedruckt in der Universitätsdruckerei Stürtz in Würzburg.
Die drei kleineren Scheiben sind Größenvarianten der
gleichen Vorlage.
Röther warb dafür mit einem Faltblatt:

Was heißt hier "pythagoräisch"?
Obwohl die Rechenscheibe sowohl in der Anleitung als auch im Prospekt als allgemeines Rechenhilfsmittel dargestellt wird, hat Röther sich bei der Konzeption seiner Scheibe vornehmlich an Aufgaben aus seiner trigonometrischen Praxis orientiert. In der ZfV hat er einige typische Anwendungen seiner Scheibe beschrieben:
"Die Berechnung einzelner Teile des rechtwinkligen Dreiecls aus gegebenen anderen mit Hilfe des pythagoräischen Lehrsatzes ist an und für sich ziemlich umständlich und hiebei die Venutzung einfacher mechanischer Rechenhilfsmittel mangels entsprechender Genauigkeit in der Regel ausgeschlossen. Beachtet man jedoch den Umstand, dass der Unterschied zwischen der grösseren Kathete und der Hypotenuse immer nur einen verhältnismäßig kleinen Bruchteil dieser Seiten darstellt, und von deren Neigung zu einander abhängig ist, so wird ein Verfahren, welches die Ausnützung dieser Tatsache zum Zwecke einfacher mechanischer Berechnung ermöglicht, um so willkommener sein, als hiebei eine Genauigkeit erreicht wird, welche allen praktischen Anforderungen entspricht.
Die vom Verfasser konstruierte "pythagoräische Rechenscheibe" enthält
ohne Beeinträchtigung der übrigen Teilungen zwei kleine mit t und u
bezeichnete Hilfsteilungen, mittels welcher
1) der Zuschlag p α zur
größeren Kathete berechnet wird, um die Hypotenuse zu erhalten und
2) der
Abzug p α, um welchen die Hypotenuse verringert werden muss, um die Kathete
zu erhalten."
Mit den "übrigen Teilungen" ist natürlich in erster Linie die logarithmisch
geteilte Skala am äußeren Rand gemeint, mit der Multiplikationen, Divisionen
und Kehrwertbildung ausgeführt werden, daneben aber auch
3) die Skala
"tang" zur Bestimmung des Tangens und Cotangens im Bereich von 6° bis 84° -
der Tangens kleinerer und größerer
Winkel kann über
die auf der Scheibe markierte Umrechnungskonstante ρ' ermittelt werden,
4) die Skala "cos aus tang", die beim Ablesen auf der Außenskala den
Umrechnungsfaktor zwischen Tangens und Cosinus liefert,
mithilfe dessen die zu einer Steigungsstrecke gehörige horizontale
Entfernung und Höhendifferenz bestimmt werden kann,
5) die Skala "sec aus sinus" die beim
Ablesen auf der Außenskala den Umrechnungsfaktor vom Sinus zum Tangens
liefert,
was zum Beispiel zur Umrechnung von prozentualer Steigung in einen
Winkel dienen kann,
6) die neue Skala "segm λ", die die Berechnung der
Fläche eines Kreissegments anhand seiner Breite und Höhe ermöglicht und
7)
die neue Skala "Logarithmus", die zu den Zahlen der Außenskala die Zehnerlogarithmen
liefert, etwa zwecks Wurzelberechnung.
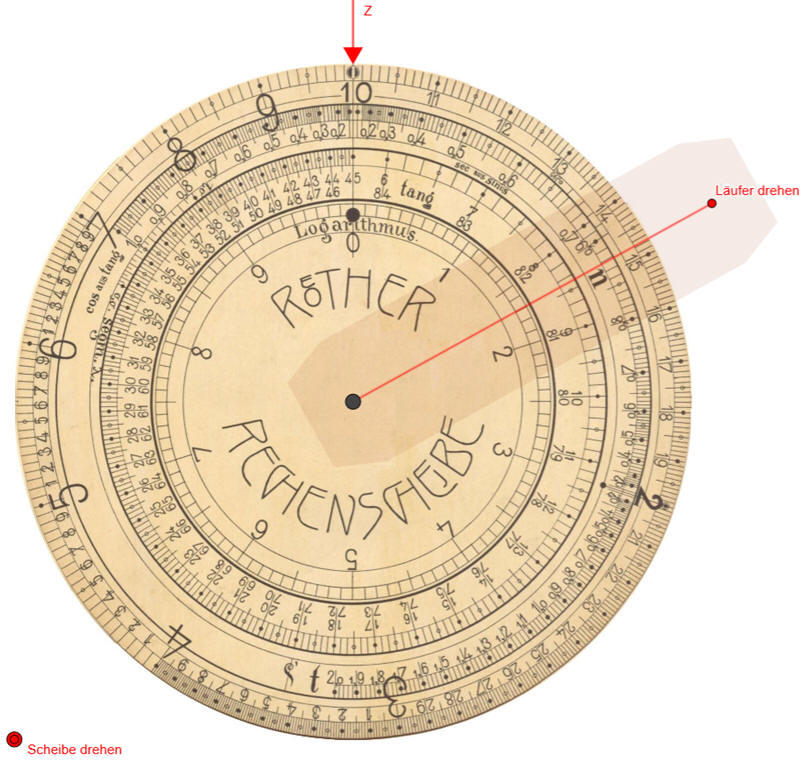
Animation
Ausführliche Anleitung
Druckvorlage zum Ausdrucken und
Nachbauen
Ein Beispiel zur t-Skala gibt die ausführliche Anleitung von 1907. Sie können die Rechnung mit der Animation nachvollziehen.

Der hier von Röther beschriebene Weg zur Berechnung der Hypotenuse eines rechtwinkligen Dreiecks ist sehr unkonventionell, aber er scheint mir weder schneller noch genauer als der formelgemäße Weg über das Quadrieren, Addieren und Wurzelziehen. Auffallend ist, dass Röther zugunsten seiner Spezialskalen auf die Implementierung einer Wurzel/Quadratskala verzichtet hat. Der übliche Rechenweg für die Aufgabe wäre auf Röthers Scheibe nur mit einem Umweg über die allgemeine Logarithmusskala möglich. Ähnlich fragwürdig erscheint mir, dass man den Sinus und Cosinus eines Winkels nur über eine Umrechnung aus dem Tangens gewinnen kann. Solche Umwege bringen zusätzliche Einstellungen und damit Zeit- und Genauigkeitsverluste mit sich.
Röthers Kollege Lüdemann nennt in einer Besprechung der Rechenscheibe in der ZfV vom Juli 1907 (S. 513) ein Beispiel, bei dem die Berechnung der Differenz zwischen Kathete und Hypotenuse über die u-Skala und die segm λ-Skala Vereinfachungen bringt. Außerdem werden dabei die auf logarithmischen Rechengeräten nicht möglichen Strichrechnungen vermieden. Es geht um „die umständliche Berechnung von Kreisabschnitten, die ja namentlich im modernen Städtebau so oft vorkommen.“

Diese Aufgabenstellung habe ich (mit anderen Zahlenwerten) auf einem Rechenstab und auf Röthers Rechenscheibe ausgeführt.
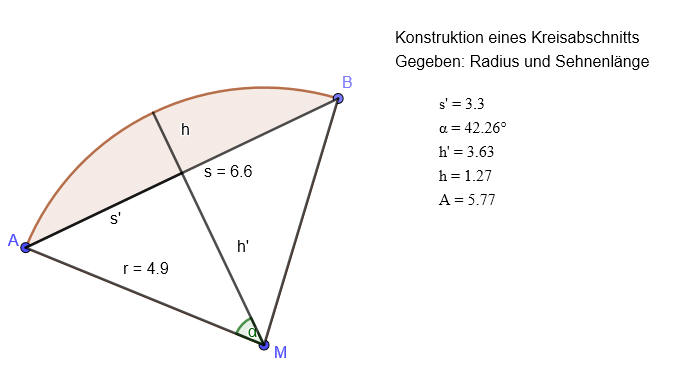
Zu berechnen sind die Höhe h
und die Fläche A eines Kreisabschnitts (farbig unterlegt).
Benötigt
werden hierfür der Radius r und die
Länge der Sehne s.
Mit einem der damals erhältlichen Rechenschieber nach dem System Mannheim (z. B. dem A.W. Faber 350) geht man so vor:
|
Man berechnet
nacheinander |
s'= 6,6 / 2 = 3,3 sin(α)=3,3 / 4,9= 0,624 α =arcsin(0,674) = 42,3° (Zunge umdrehen, Wert übertragen) cos(42,3°) = sin(47,7°) = 0,741 (Subtraktion, Wert übertr.) h'= 0,741* 4,9 = 3,63 (Zunge umdrehen, Wert übertragen) h = 4,9-3,63 =1,27 (Subtraktion) |
Mein Ergebnis ist tatsächlich auf zwei Stellen korrekt. Allerdings brauchte ich für die Einstellungen eine Lupe.
| Um die Fläche A des Kreisabschnitts zu
bestimmen, nimmt man - die Fläche des kompletten Kreisausschnitts A1= r²*π/360*2α - die Fläche des Dreiecks zwischen Sehne M: A2=s/2*h' - und subtrahiert A = A1 - A2 |
A1 = 4,9²*π/360*84,6 = 17,68 (2 Skalensprünge) A2= 3,3 * 3,63 = 11,98 (Neueinstellung) A = 17,68 - 11,98 = 5,70 (Subtraktion) |
Das sind bei Wiederverwendung von notierten Zwischenergebnissen zehn Punktrechnungen, zwei Skalensprünge (Übertragung eines Zwischenergebnisses auf eine andere Skala) und drei Subtraktionen. Die Subtraktionen müssen im Kopf oder auf Papier erfolgen, da Rechenscheiben keine Strichrechnung erlauben. Das Endergebnis weist eine Ungenauigkeit von 1,2% auf.
Den
etwas anderen Rechenweg mit der Röther Rechenscheibe kann
man an der Animation
nachvollziehen.
Auf dem Original (Durchmesser 11 cm) lassen sich Einstellungen jedoch
exakter vornehmen.
| - Man teilt s durch
2, dann durch r. - Das Ergebnis entspricht sin(α). - Diesen Wert sucht man auf der Spezialskala u auf und stellt den Läufer darüber. - Dann dreht man die kleinere Kathete unter den Läuferstrich - und erhält bei der Marke Z die Höhe des Segments |
s' = 6,6 / 2 = 3,3
(6,6 auf Z, L auf 2, 10 unter L -> Z=3,3) s'/r = 3,3 / 4,9 = 0,67 (L auf 4,9; 10 unter L -> Z=0,67) Läufer auf 0,67 der u-Skala (Skalensprung) 3,3 der Hauptskala unter L h = 1,27 bei Z abgelesen |
| Die Fläches A des
Kreisabschnitts kann
man so bestimmen: - man berechnet h/r, - sucht das Ergebnis auf der Skala segm λ und stellt es auf Z - und berechnet die Fläche mit A = segm(λ)*s*h |
λ=h/r =1,27 / 4,9 = 0,26 segm(0,26)=0,687 auf Z (Skalensprung) A = 0,687 * 6,6 * 1,27 = 5,73 |
Insgesamt sind das nur fünf Punktrechnungen und zwei Skalensprünge. Außerdem spart man die Subtraktionen ein, d.h. man kann die komplette Rechnung mit der Rechenscheibe ausführen und benötigt keine Nebenrechnungen auf Papier. Da die Skala der Rechenscheibe etwas länger ist als die des Rechenstabs (35 cm gegenüber 25 cm), sollte sie genauere Ergebnisse liefern, die Genauigkeit meiner Rechnung war bei sorgfältiger Einstellung auch mit nur 0,7% Abweichung minimal besser als beim Rechenstab. Nach den Angaben in der Anleitung (1:1200 pro Rechnung bei der 11-cm-Scheibe) sollte die addierte Abweichung der sechs Operationen allerdings maximal 0,5% betragen. Das Ergebnis entsprach also nur annähernd den Erwartungen.
Die Handhabung meines Exemplars der Rechenscheibe war insgesamt weniger angenehm als die meines Rechenschiebers. Zwar brauchte ich dank der sehr klaren Skala keine Lupe, aber die Reibung zwischen Scheibe und Grundplatte war zu hoch. Es war eine unangenehme Pfriemelei, die dünne Scheibe zum Drehen am Rand anzuheben und den Läufer dabei exakt zu fixieren. Zwei jüngere Exemplare der Scheibe, die ich später ausprobieren konnte, liefen wesentlich glatter als mein Exemplar. Die Scheibe ließ sich hier leicht mit aufgelegtem Finger unter dem mit dem Daumen fixierten Läufer durchdrehen.
An die Arbeitsweise mit Skala, Marke und Läufer musste ich mich erst gewöhnen. Ich habe mit der Rötherscheibe zunächst länger gebraucht als mit dem Rechenschieber, fand die Handhabung aber mit der Zeit recht praktisch. Röther jedenfalls war sicher:

Die Frage, ob "die umständliche Berechnung von Kreisabschnitten, die ja namentlich im modernen Städtebau so oft vorkommen" - also der Berechnung von Grundstücksgrößen an Straßenkurven - die Anschaffung der Scheibe und die Einarbeitung in proprietäre Verfahren rechtfertigt, musste der potentielle Käufer beantworten. Dass der Leidensdruck dieser Umständlichkeit für den Erfinder die einzige Motivation war, in Konkurrenz zu einigen etablierten Firmen ohne große Werkzeugausstattung spezielle Skalen zu konzipieren die zugehörigen Tabellen mit mehrstelliger Genauigkeit zu berechnen, tausende Skalenstriche präzise von Hand zu zeichnen und die Scheibe zu Anfang auch noch selbst herzustellen und zu vertreiben, darf man bezweifeln. Röthers Antriebskräfte waren wohl eher fachlicher Ehrgeiz und Spaß am Design. Neben der Rechenscheibe und den Maßstäben hat er auch einen Neigungsmesser und ein "Orientierungs- und Winkelinstrument" konstruiert und allgemeine Artikel über Fachfragen publiziert.
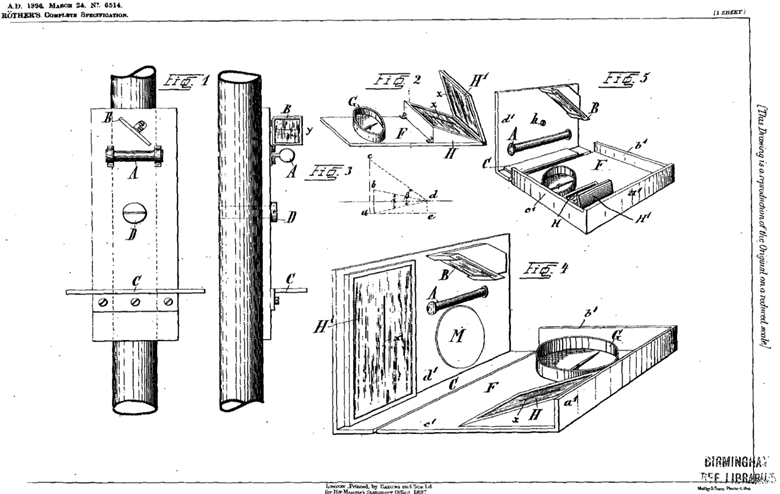
1896 erhielt Röther in England das
Patent GB189606514 auf einen
Neigungsmesser
zum Abstecken
oder Messen eines Gefälles
Für den Verschönerungsverein Würzburg zeichnete Röther im Jahr 1907:
Die Rundsicht
von der Frankenwarte
Wie wär's mit einer Rechenmaschine?
In "Stahlgehirne" (Kapitel 3.3) ist nachzulesen , dass die "Landmesser" schon vor dem ersten Weltkrieg auch von den Herstellern mechanischer Rechenmaschinen stark umworben wurden. Diese boten für Standardaufgaben Formulare an, auf denen Arbeitsabläufe vorgegeben und nur noch individuelle Maße einzutragen und durchzurechnen waren. Im Gegensatz zur Arbeit mit logarithmischen Rechengeräten mit trigonometrischen Spezialskalen waren hierfür aber neben der schweren Rechenmaschine auch nach wie vor Zahlentafeln zum Nachschlagen trigonometrischer Werte erforderlich. Im gleichen Heft der ZfV (Dezember 1899 S. 687-696), in dem Röther seine Rechenscheibe zum ersten Mal zum Verkauf angeboten hatte, wurde von einem seiner Kollegen die schwergewichtige Multipliziermaschine "Millionär" von einem Fachkollegen Röthers hoch gelobt. Einem anderen Rezensenten erschienen Rechenmaschinen zwar genau, aber "viel zu theuer und langsam", und für die meisten Geometer waren sie wohl unerschwinglich.
Röther scheint sich jeoch auch mit Rechenmaschinen beschäftigt zu haben: In der Novemberausgabe 1907 der ZfV lieferte er eine Zahlentafel mit vierstelliger Genauigkeit für den Faktor Lambda (dem Verhältnis zwischen der Fläche eines Kreisabschnitts und dem umschließenden Rechteck), und er adressierte sie ausdrücklich auch an Maschinenbenutzer. Mit welchen Hilfsmitteln er selbst die Formel tausend mal durchgerechnet hat, lässt er offen. Da aber selbst seine Präzisionsrechenscheibe für eine einzelne Rechnung nur auf vier Stellen genau rechnete, muss er wohl, um für die Ergebnisse einer komplexeren Formel eine vierstellige Genauigkeit zu garantieren, selbst auch Zugang zu einer Rechenmaschine gehabt haben.

Nach dem ersten Weltkrieg erschien 1921 eine Neuauflage der Rechenscheibe zusammen mit einer 11-seitigen "Anleitung für den Gebrauch der verbesserten Rötherschen Rechenscheibe" von Anton Bayr, heute noch auszuleihen in der Bibliothek des deutschen Museums. Bayr teilt darin mit, dass er als früherer Mitarbeiter Röthers auf vielfaches Drängen hin dessen Rechenscheibe verbessert und neu aufgelegt habe, "nachdem sie durch die Kriegszeit und durch vorzeitiges Hinscheiden von Röther in Vergessenheit kam".
Die Rechenscheibe von Bayr besitzt einen übersichtlicheren Aufbau als die Rötherscheibe und ist durch eine dickere verschraubte Achse und verminderte Reibung zwischen Scheibe und Grundplatte leicht mit aufgelegtem Finger zu drehen. Die Skalen "cos aus tang", "sec aus sin" und "segm λ" hat Bayr durch eine native Skala für sin/cos ersetzt. Die Logarithmusskala ist in besserer Auflösung nach außen auf die Grundplatte gewandert. Insgesamt hat Bayr sich dem klassischen Skalensatz wieder mehr angenähert, eine Quadrat- oder Wurzelskala gibt es aber immer noch nicht. Allerdings fehlt dem neuen Entwurf etwas vom Charme des Röther'schen Jugendstil-Designs. Die Scheibe trägt die neue Gebrauchsmusternummer DRGM 793344, aber keine Herstellermarkierung.
►
AnimationAnleitung
Die Bayr-Scheibe scheint ebenfalls rasch in Vergessenheit geraten zu sein. In einer Marktschau von der Allgemeinen Vermessungs-Nachrichten von 1924 mit insgesamt elf Rechengeräten für Vermesser tauchen die Namen Röther und Bayr nicht mehr auf.
Auch Konkurrenzmodelle blieben wohl Eintagsfliegen: Die von Dipl. Ing K. Gampert für das Bayerische Landesvermessungsamt (also nach 1915) konstruierte "Pythagoras- und Rechenscheibe" aus der ►Sammlung von Wilfried Denz (►Animation) besaß einen ähnlichen Aufbau wie die Rötherscheibe. Sie verzichtete jedoch ganz auf Winkelfunktionsskalen und ermöglichte zusätzlich zum logarithmischen Multiplizieren und Dividieren lediglich über zwei spiralförmige Skalen die Berechnung der dritten Seite im rechtwinkligen Dreieck mit immerhin dreistelliger Genauigkeit. Die Arbeitsweise bei den beiden pythagoräischen Skalen ist ähnlich wie beim Rechenstab mit zwei Skalen. Nehmen wir z.B. ein rechtwinkliges Dreieck mit den Seitenlängen 30, 40 und 50: Man stellt die 30 der inneren Skala gegenüber der roten 0-Marke der äußeren Skala. Dann sucht man die 40 auf der äußeren Skala, stellt den Läufer darauf und liest ihr gegenüber auf der inneren Skala die Hypotenusenlänge 50 ab (30²+40²=50²). Kathetenberechnung funktioniert umgekehrt: Man sucht eine Kathedenlänge auf der äußeren Skala, stellt den Läufer drüber und dreht die Hypotenusenlänge der inneren Skala darunter. Dann liest man die anderen Kathetenlänge gegenüber der 0-Marke ab. Liegen die Werte auf verschiedenen Spiralwindungen, so ist der Versatz bei der Addition entgegengesetzt und bei der Subtraktion gleichgerichtet. Handwerklich scheint das Gerät im Prototyp-Stadium steckengeblieben zu sein, in Bezug auf Vielseitigkeit war es gegenüber Röthers Scheibe ein Rückschritt.
Sehr viel professioneller wirkt da der Rechenschieber R.R. Py-Lo (pythagoräisch-logarithmisch) für Eisenbahn-Landmesser von Seiffert, den Reiss 1924 auf den Markt brachte und der später von Wichmann vertrieben wurde. Aber er ist heute ebenfalls bei Auktionen und bei Sammlern kaum zu finden. Offenbar arbeiteten die Geometer lieber mit den trigonometrischen Standardskalen.
Letzten Endes blieb von den pythagoräischen Geräten nur eine Art Fußnote übrig: Im Jahre 1934 wurde das Rietz-Skalensystem der Standard-Rechenstäbe im System Darmstadt um die Skala" P √(1-x²) ergänzt. Sie gestattet die direkte Umrechnung zwischen Sinus und Cosinus und ist mit keiner der Röther'schen Skalen identisch.
Auch Röthers von Boucher übernommenes Bedienungskonzept mit einer einzelnen logarithmischen Skala, einer festen Marke und einem transparenten Läufer konnte sich auf Dauer nicht durchsetzen. Fast alle anderen davor und danach in Deutschland angebotenen Rechenscheiben besaßen zwei gegeneinander drehbare logarithmische Skalen. Das Skala-Marke-Läufer-Konzept überlebte jedoch bei den Fowler-Rechenuhren in England und es erlebte in der Sowjetunion noch 1965 eine Renaissance mit der offenbar millionenfach verbreiteten Rechenuhr Moskp KL-1.
Während Teile der Geisteswelt am Anfang des 20. Jahrhunderts den "Untergang des Abendlands" heraufdämmern sahen, war die "Gründerzeit" gleichzeitig von rasender technischer Entwicklung geprägt. Donatus Röther scheint einer der rastlosen Erfinder und Tüftler gewesen zu sein, die Spaß an der Technik hatten und neue Ideen um die Wette produzierten.
Glanzstücke jeder Sammlung sind die
Meilensteine und die Exoten. Röthers Rechenscheibe gehört wohl eher zu den
Exoten.
Rechenwerkzeug.de