Rechenstäbe und Rechenwalzen

Addieren geht einfacher als multiplizieren und subtrahieren geht viel einfacher als dividieren - eine Binsenweisheit.

Auf der Suche nach schnellen und wenig fehleranfälligen Rechenmethoden entdeckte man eines Tages, dass man Multiplikationen durch Additionen und Subtraktionen durch Divisionen ersetzen kann:

100 * 1000 = 10² * 10³ = 10²⁺³ = 10⁵ = 100000

512 : 64 = 2⁹ : 2⁶ = 2^9-6 = 2³ = 8

Im Jahre 1614 veröffentlichte Lord Napier of Merchiston die erste Logarithmentafel. Jeder Zahl wurde darin die Hochzahl zugeordnet, mit der eine feste Basis potenziert werden musste, um die entsprechende Zahl zu erhalten.
Wollte man zwei Zahlen multiplizieren, so schlug man in der Tabelle die Hochzahlen (logarithmen) der beiden Faktoren nach,  addierte diese und suchte anschließend die Zahl, deren Logarithmus man bei der Rechnung erhalten hatte. Dieses Verfahren ist unabhängig von der Basis mit der der Logarithmus gebildet wird, schon 1615 setzte sich aber die 10 als Basis durch.

	Zahl	Logarithmus	Multiplikation: log(2) = 0,301 log(3) = 0,477 0,301+0,477 = 0,778 0,778 = log(6) Division: log(8) = 0,903 log(4) = 0,602 0,903-0,602=0,301 0,301 = log(2)
	1	0
	2	0,301
	3	0,477
	4	0,602
	5	0,699
	6	0,778
	7	0,845
	8	0,903
	9	0,954
	10	1

Nun weiß jeder, dass man Zahlen addieren kann, indem man zwei Zollstöcke aneinanderlegt 2 cm + 3 cm = 5 cm:

Verwendet man für diese Operation eine logarithmische Skala, so wird aus dieser Operation eine Multiplikation. Die  logarithmische Skala reicht von 0 bis 1. Die Abstände ihrer Teilstriche sind entsprechend den Logarithmen gesetzt, aber mit den zugehörigen Zahlen beschriftet. Aneinandergelegt werden auf der folgenden Skala die Logarithmen 0,301 + 0,477 = 0,778. Auf der Skala erschein die Rechnung  2 * 3 = 6.

Der Rechenstab liefert nur die Ziffernfolge des Ergebnisses. Die Größenordnung ist durch Überschlag zu ermitteln. Die abgebildete Rechnung könnte also ebenso gut 20 * 30 oder 0,2 * 30 oder 200 * 30000 lauten. Die Skala ist im Übrigen endlos zu denken: Hinter der 10 und vor der 1 liegt dieselbe Skala. Wenn, wie bei der Aufgabe 2 * 8, der zweite Faktor hinter der 10 der ersten Skala liegt, stellt man die 10 auf die 2 und liest links ab. Diesen Vorgang bezeichnet man als "Durchschieben".

Die ersten Rechenstäbe besaßen nur eine Skala. Man rechnet mit einem Stechzirkel. Um 3 * 2 zu rechnen, greift man den Abstand zwischen 1 und 3 ab und überträgt ihn hinter die 2. Doch die Arbeit mit dem Stechzirkel legt noch eine andere Interpretation nahe. Betrachtet man Zahlenpaare, die auf der Skala den gleichen Abstand haben, so entdeckt man, dass diese Zahlenpaare der Proportionsgleichung a : b = c: d genügen. 1 verhält sich zu 3 wie 2 zu 6. Viele Aufgaben des täglichen Lebens (die sog. Dreisatzaufgaben lassen sich auf diese Weise lösen: 37,5 Liter Benzin verhalten sich zu 525 km Fahrstrecke wie x Liter zu 100 km Fahrstrecke. Man greift auf der Skala den Abstand zwischen 3,75 und 5.25 ab und überträgt ihn vor die Zehn. Der Durchschnittsverbrauch auf 100 km beträgt also 7 Liter.

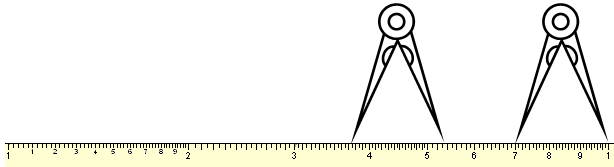
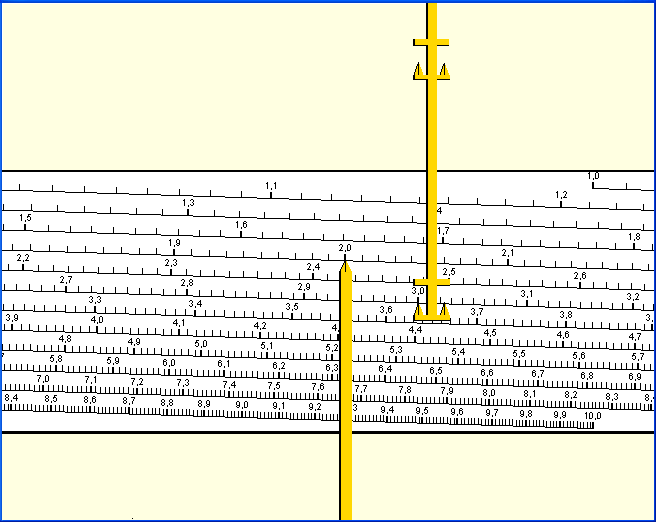
Das größte Problem der Rechenstäbe ist ihre beschränkte Genauigkeit. Normale Rechenstäbe sind etwa 25 cm lang und man kann auf ihnen mit zwei- bis dreistelliger Genauigkeit rechnen. Auf einer kreisförmigen Rechenscheibe mit einem Durchmesser von 30 cm (z.B. der großen Tröger-Rechenscheibe) lässt sich immerhin schon eine  knapp 72 cm lange Skala unterbringen. Mit wachsenden Anforderungen genügte das nicht mehr. Und es war auch nicht nötig. Das Prinzip der Übertragung von Proportionen ließ sich nämlich auch auf Skalen übertragen, die schraubenfederförmig um einen Zylinder gewickelt oder in achsenparallelen Teilstücken auf einen Zylinder montiert waren. Hier werden zwei Zeiger auf eine feste Proportion eingestellt und dann die Skala unter ihnen verschoben:

Bewegliche Simulation zum Download (Windows-Programm)

Rechenwerkzeug.de