Mess- und Zeichengeräte

Analog funktionierende Mess- und Zeichengeräte

Ein Thermometer mit einer Doppelskala in Celsius und Fahrenheit ist kein Rechenhilfsmittel im strengen Sinne, da die beiden Skalen lediglich dazu dienen, Messwerte in der gewünschten Einheit abzulesen. Es kann aber zum Rechenhilfsmittel werden, wenn man es zum Umrechnen benutzt. Beim genaueren Hinsehen entdeckt man, dass in viele Mess- und Zeichengeräte Umwandlungs- und Rechenvorgänge bereits fest integriert sind. Ohne den Umweg über die numerische Darstellung (also auch unter Vermeidung des Zahlenrechnens) lassen sich Größen umformen und physikalische Vorgänge in Echtzeit modellieren, indem man Skalen dehnt, Getriebe konstruiert oder Hebel zur Bildung von Proportionen ausnutzt. So wird ein einfaches Messgerät zum Analogrechner. Die große Zeit der reinen Analogrechner ist vorbei. Digitale Steuerungen sind heute in der Regel leichter zu konstruieren, universell zu programmieren und billig herzustellen. Zur Messung analoger Größen integriert man Analog-Digital-Wandler, zur Steuerung analoger Ausgänge Digital-Analog-Wandler als Schaltkreise in Chips. Die Verarbeitung der Diaten erfolgt aber in der Regel digital. Prozessoren und Speicher sind winzig klein und so schnell, dass die Programme gefühlt in Echtzeit ablaufen. Und die Größe der Geräte wird in der Regel nicht durch die Verarbeitungsstufe, sondern durch Eingabe- oder Anzeigeelemente vorgegeben.
	Zollstock handgefertigt vor 1900	Vier Elfenbeinstäbe verbunden mit drei Messinggelenken. Aufgeklappt 1 Fuß (hier 31,2 cm) lang. Drei verschieden genormte Zollskalen, jeweils eingeteilt in Achtelzoll (1" = 26 mm, 1" = 25,6 mm, 1" = 23,5 mm bzw. 11/12 von 25,6 mm), Außerdem eine Zentimeterskala. Der Zollstock ist sowohl zum Messen wie zum Umrechnen der verschiedenen Einheiten geeignet.
	Proportionalzirkel Messing "Original Riefler" von R.Reiss, Liebenwerda etwa 1920	Proportionalzirkel nach Jost Bürgi (1552-1632) Mit den beiden Skalen des Geräts, kann der Proportionalzirkel dazu verwendet werden, Zeichnungen in variablem Maßstab zu vergrößern oder zu verkleinern. Ebenso ist es möglich, Strecken in 2 bis 10 und Kreise in 3 bis 20 gleiche Teile aufzuteilen. Es gab Vorläufer mit festem Maßstab, sog. Reduktionszirkel.
	Compas de proportion Messing Länge: 1 pied de roi Michel Grilliet Paris Frankreich etwa 1770 Anwendung Animation	Proportionalzirkel (auch "Proportionalwinkel") nach Galilei (1564-1642) und anderen Lehrern. Dient zum Abgreifen, Messen und maßstäblichen Übertragen von Strecken und Winkeln mittels Stechzirkel. Übliche Skalenausstattung: - Les Cordes (Winkelmessung über Sehnen), - Les Egales (proportionale Änderung von Strecken) - Les Plans, Les Solides (Flächen und Körper) - Les Poligones (Regelmäßige Vielecke) - Les Metaux (Metallbestimmung) - Poids des boulets, - Calibre des pieces (Geschosskaliber)
	Sector Elfenbein. Länge: 1 engl. Fuß Williams & Haydon London etwa 1830 Skalen 2	Proportionalzirkel, wie er in England um 1624 von Edmund Gunter beschrieben wurde. Über die zum Konstruieren erforderlichen Skalen hinaus enthält der Sector die von Gunter entworfenen Funktionsskalen (Sinus, Tangens, Logarithmus) zur analogen Durchführung numerischer Rechnungen mittels Stechzirkel. ►mathsinstruments ►The Works of Edmund Gunter ►Scheffelt: Instrumentum Proportionum
	Konstruktionswerkzeug Kirschbaum- oder Lindenholz Hamburg 19. Jahrhundert	Nach dem Vorbild englischer Mess- und Rechen-hilfen gefertigtes Lineal. Es enthält je eine Längenskala in dänischen (314 mm) und schleswig-holsteinischen Fuß (287 mm), eine logarithmische Skala über zwei Dekaden und eine Reihe von Sinusskalen zum Konstruieren von Winkeln, außerdem einen Transversal-Maßstab zum genauen Messen und Zeichnen. Alle oft gebrauchten Punkte sind mit eingeschlagenen Metallstiften ausgestattet, sodass sie mit einem Stechzirkel leicht abgegriffen werden können. Näheres
	Gunter Rule Buchsbaumlineal 24 Zoll zum Messen und Rechnen Logarithmische Skalen 1624 zunächst auf Sector später als Lineal mit 22 Skalen Bis ins 19. Jahrhundert Hilfsmittel zur Navigation Ohne Herstellermarkierung Großbritannien ca. 1830	vorn: Logarithmische Skala Num von 1 bis 100, außerdem Skalen Sin, Tan, SR, TR, VS und Meri und Eq Parts (für Mercatorkarten). hinten: lineare Zollskala von 24 bis 0, darunter links lineare Skala von 10 bis 0 mit Hilfslinien zum Abgreifen dezimaler Zwischenwerte, rechts Lea (lineare Bezugsskala), Cho (Grad), Rum (Kompassmarken 90°=8 Rumb), Sin, Tan, ST, M*L (Miles of Longitude, Abstand zweier Längengrade gegebener Breite), Cho. ►Ähnliche Geräte ►Anwendung ►Gunter Rules in Navigation
	Protractor Transporteur mit Transversalmaßstab Buchsbaumholz Großbritannien 19. Jahrhundert	Der Protractor ist die britische Version eines Winkelmessers. Winkel können damit auf ähnliche Weise wie mit einem Geodreieck oder Halbkreswinkelmesser gezeichnet, aber auch mithilfe eines Zirkels und der "Chord"-Skala konstruiert werden. Auf der Rückseite können Zollbruchteile mit dem Zirkel abgegriffen werden. Solche Lineale wurden im 19. Jahrhundert in der Regel im Set zusammen mit einem Sector, einem verstellbaren Parallelenlineal und mehreren unterschiedkichen Zirkeln verkauft.
	Das mathematische Aschenbrödel oder der Ingenieur-Messknecht Maximilian Robert Pressler Leipzig Baumgärtner's Buchhandlung 1870 ►Volltext	Faltbare Karte mit Lot als Höhenmesser mit optionalem Visierzubehör, dazu analoge Skalen und digitale Tabellen 128 Seiten Anleitung mit diversen Tabellen und Beispielrechnungen zu Trigonometrie, Flächen- Volumen- und Gewichtsberechnung, Umrechnung von Einheitenen und Währungen, aber auch Zins- Renten- und Kalenderrechnung. 4. Auflage eines ähnlichen Buches, das ab 1850 unter dem Titel "Presslers mathematische Brieftasche" erschienen war.
	Messzange Genauigkeit 1/10 mm ca. 1920	Durch proportionale Vergrößerung der Skala um den Faktor 4 wird eine höhere Genauigkeit erreicht.
	Schieblehre OMC Fontana ca. 1975	Mit einer Schieblehre kann man die Dicke kleiner Gegenstände oder den Innen- und Außendurchmesser von Rohren auf 1/20 mm genau messen. Die Skala besitzt einen sogenannten Nonius - eine um 0,5 mm versetzte und um 5% gekürzte Gegenskala. Sie wird dort abgelesen, wo zwei Skalenstriche genau übereinstimmen. Der gemessene USB-Stecker ist 1,24 mm breit. ►Wikipedia
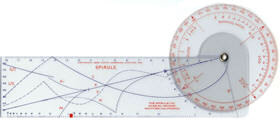
	Spirule Walter R. Evans USA 1951	Kombination aus Winkelmesser und Lineal zur Analyse und Anpassung von ►Wurzelortskurven aus der Regelungstechnik. Die für das Instrument namengebende logarithmische Spirale S ermöglicht in Verbindung mit diversen Skalen die numerische Bestimmung von Pol- und Nullstellen der Kurve und deren Veränderung durch die analoge Addition und Multiplikation von Vektoren. Manual 1 ►Manual 2
	Inklinometer (Slope Meter) Hendrick Mfg. Co USA	Nach Aufsetzen der rechteckigen Bronzetafel auf eine schräge Fläche kann man an der Spitze des frei beweglichen Zeigers die Neigung der Fläche in Grad ablesen. Eine eingravierte Tabelle rechnet die ermittelte Neigung in prozentuale Steigung um. In einer zweiten Spalte kann man ablesen, um wie viel Zoll die Fläche auf einen Fuß horizontalen Abstand ansteigt oder fällt. 17° Neigung = 30,57% Steigung = 3 ²¹/32 Zoll Niveauunterschied pro Fuß. Das Gerät diente speziell dazu, die Gefälle am Rand von Kohletagebaugruben abrutschsicher anzulegen.
	Ringsonnenuhr nach einem Vorbild aus dem 17. Jahrhundert Kala 2020	Im Unterschied zu einfachen Sonnenuhren berücksichtigt eine Ringsonnenuhr die durch die Schräge der Erdachse bedingten jahreszeitlichen Abweichungen des Sonnenstands (± 10 min). Man stellt den Aufhänger auf den Breitengrad des Ortes und den schwarzen Schieber auf den laufenden Monat ein und dreht den Ring so, dass das Abbild des Loches auf dem Äquatorring sichtbar wird. Dadurch steht der Meridianring in Nord-Süd-Richtung und der Lichtpunkt unter der aktuellen wahren Ortszeit. ►Helios Sonnenuhren
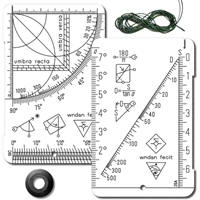
	Quadrant-Telemeter Wndsn 2015 ►Beschreibung	"Scheckkarte" zum Visieren und Messen Vorderseite (Quadrant): Messung von Winkeln zur Vertikalen oder Horizontalen und der prozentualen Steigung Rückseite (Telemeter): Messung von Winkelgröße oder Winkelabstand anvisierter Objekte und Umrechnung von Winkeln in Längen mittels Nomogramm
	Kurvimeter Werbegeschenk von VW Deutschland ca. 1980	Das Gerät wird über Wegstrecken auf Karten abgerollt und zeigt für die Maßstäbe 1:25000, 1:50.000, 1:75.000, 1:100.000, 1:150.000, 1:300.000, 1:500.000 und 1:800.000 die tatsächliche Streckenlänge sowohl gerader als auch gekrümmter Linien an.
	Roller Rule The Pencil with a Brain USA um 1950	Ein Reibrad, das über gerade oder gekrümmte Linien abgerollt werden kann. Die zurückgelegte Strecke (bei jeder Umdrehung 2 Zoll) wird am Reibrad auf 1/8 Zoll genau angezeigt. Über eine Spindel wird ein Zeiger auf einer Skala bewegt und zeigt bis zu 36 ganze Zoll (90 cm) an. Der untere Teil verbirgt einen Drehbleistift. Der Anleitung zufolge kann es sogar addieren, subtrahieren, multiplizieren und dividieren, ist aber durch Kopfrechnen locker zu schlagen.
	Maßstabsskalen Aristo Germany	Skalen zum direkten Ablesen von Abständen auf Plänen im Maßstab 1:10, 1:15, 1:20, 1:25, 1:30, 1:33 1/3, 1/40, 1:50, 1:75, 1:125
	Maßstabsskalen Soldatenausrüstung ca. 1940	Topographische Karte 1:100.000 und Maßstabsskalen 1:100.000, 1:25.000, 1:50.000 jeweils ausgehend von einem Eckpunkt
	Pantograph Deutschland ca. 1970	Gerät zum Vergrößern oder Verkleinern von Zeichnungen mit einstellbarem Maßstab (1:2; 1:2,25; 1:2,5; 1:2,75; 1:3; 1:4; 1:5; 1:6; 1:7; 1:8; 1:10). Im Unterschied zum Proportionalzirkel bleiben hier entsprechende Strecken automatisch parallel. Streckenteiler
	Gerber Variable Scale The Gerber Scientific Instrument Company Hartford Connecticut 1953-1995 Anwendung	Lineal mit einer variablen Skala, aufgetragen auf einer 1 Zoll langen dreieckigen Spiralfeder mit 100 Windungen. Die Feder lässt sich auf 10 Zoll ausziehen. So erhält man eine Skala von 0 bis 10, die an beliebige Maßstäbe angepasst und direkt zum Messen oder Zeichnen verwendet werden kann. Außer der variablen Skala befinden sich auf dem Lineal drei festen Skalen. ►Näheres ►Berechnung von Wurzeln komplexer Zahlen ►Ähnliches Gerät (Centifix)
	Hyperbeltafel Maßstab 1:1000 M. Kloth um 1900	Hyperbeltafeln sind Glasplatten mit aufgedruckten Hyperbelscharen. Sie waren erhältlich in gängigen Landkartenmaßstäben und dienten zur Flächenberechnung von Grundstücken. Legt man die Glasplatte so auf ein Dreieck, dass dessen eine Seite parallel zur y-Achse des Diagramms ist und je eine Ecke auf den beiden Achsen liegt, so kann man an der dritten Ecke des Dreiecks dessen Flächeninhalt ablesen. ►Rechnerlexikon
	Polarplanimeter A.Ott, Kempten SN 38651 ca. 1950	Ein analoger Integralrechner, mit dem man Flächeninhalte messen kann. Der Rand einer Figur wird mit einem Stift umfahren. Dabei registriert eine mitlaufende Rolle die Dreh- und Schubbewe-gungen des Fahrarms. Während die Drehbewe-gungen sich in der Summe gegenseitig aufheben, ergibt die Summe der Schubbewegungen ein Maß für den Flächeninhalt der umfahrenen Figur. Dieser kann auf drei bis vier Stellen genau abgelesen werden. ►Beschreibung von Wolf-G. Blümich ►Andere Fabrikate
	Belichtungsmesser Deutschland ca. 1925	Optischer Belichtungsmesser. Eine Reihe von Öffnungen wird zunehmend abgedunkelt. Anhand der letzten noch sichtbaren Öffnung kann man beim Durchschauen die Umgebungshelligkeit abschätzen. Diese rechnet man mittels eines drehbaren Skalenrings in eine beliebige Zeit-Blenden-Kombination um.
	Pedometer Henri Chatelain Palo Co France ca. 1900	Das Pedometer, heute ein Fitnessgerät, diente früher zur Entfernungsmessung. Pedometer sind schon im 16. Jahrhundert bekannt. ►Wikiipedia Mein Pedometer wurde in Frankreich für den englischen Markt hergestellt. Ein beim Gehen schwingendes Pendel zählt digital die Schritte und rechnet sie über ein Getriebe in Yards und Meilen um. (1760 Yards=1 englische Meile). Diese werden analog angezeigt. Über einen kleinen Hebel, der bei aufgeklapptem Rückdeckel zugänglich ist, kann das Gerät an unterschiedliche Schrittlängen angepasst werden. ►Chatelain
	Gebühreneinheitenzähler in der Vermittlungsstelle Deutsche Bundespost 1964	Im Jahr 1964 gab es in den Vermittlungsstellen der Post Anzeigetafeln jeweils etwa hundert mechanischen Zählwerken, eins pro Anschluss. Ein Elektromagnet erhielt während jedes Telefonats abhängig von der Zone (lokal, reginal, national, international) in Sekunden- oder Minutenabständen einen elektrischen Impuls. Dieser betätigte einen kleinen Schalter im Zählwerk. Die Anzahl der Impulse wurde mechanisch digital gezählt. Am Ende des Monats wurde die Anzeigetafel fotografiert und die Gebühreneinheiten mit dem Kunden abgerechnet.
	Gebührenzähler für Kunden Deutsche Bundespost ca. 1970	Mechanischer Kurzzeitmesser digital vorwärtszählend mit analoger Rechenfunktion. Die Deckscheibe mit Indexstrich wird nach links bis zum Anschlag gedreht, und mit einem Druck auf den Knopf in der Mitte wird beim Beginn des Gesprächs der Ablauf gestartet und gestoppt. Auf der Skala ganz außen kann man dann die Gesprächsdauer ablesen. Die anderen Skalen nennen dazu den Preis des Gesprächs bei verschiedenen Zeittakten. (Die rote Zahl vor jeder Tabellenzeile gibt den "Zeittakt" an, also wie viele Sekunde man für eine "Tarifeinheit" zum Preis von damals 21 Pfennig telefonieren konnte.)
	Taktgeber E. Zimmermann Leipzig Berlin um 1900	Dies ist ein digitaler Taktgeber für elektrische Impulse aus dem Anfang des 20. Jahrhunderts. Ein Pendel, das von einer Feder in Gang gehalten wird, lässt eine Nockenscheibe in 60 Sekunden einmal rotieren. Auf deren äußerstem Umfang sitzen 60 Pins, weiter innen gibt es Kreise mit 30, 20, 15, 10, 5, 4, 3, 2, 1 Pins, die entsprechend viele Impulse pro Minute auslösen. Wie bei einem Metronom lässt dich außerdem das Gewicht am Pendel verschieben und der Impulsabstand analog feinregulieren.
	Fliegeruhr Jaragar China 2019 28,50 €	Mechanische Automatik-Armbanduhr mit ►Tachymeterskala zum Ablesen der Geschwindigkeit beim Zurücklegen einer bekannten Strecke und einer verstellbaren logarithmischen Skala zur Umrechnung auf andere Strecken. Mittels einer logarithmischen Skala kann man Umrechnungen vornehmen. Auch die Uhr enthält eine Rechenmaschine: Sie zählt die Bewegungen einer Unruh und rechnet sie über ein Getriebe in Sekunden, Minuten und Stunden um, die sie analog anzeigt.
	Fahrradtacho mechanisch China 2019 9,90 €	Ein analoger Differentialrechner. Die Umdrehung des Rades wird mit einem Haken abgegriffen und mit einer Welle zum Tacho übertragen. Dieser rechnet über ein kleines Getriebe die Anzahl der Radumdrehungen in Kilometer um und gibt sie auf ein Zählwerk. Eine Metallglocke dreht sich dabei gleichzeitig um einen an der Tachonadelachse befestigten Dauermagneten und erzeugt dabei magnetische Wirbelströme. Abhängig von der Drehzahl wird die Achse gegen eine Feder unterschiedlich stark mitgenommen. Der Zeiger des Tachos bewegt sich dabei über eine Skala (UpM / km/h).

Rechenwerkzeug.de