Ein Mess- und Zeichenlineal aus Norddeutschland

Dieses Lineal habe ich bei einem Verkäufer aus Hamburg erstanden, der es auf dem Dachboden gefunden hatte. Wie der Galilei'sche  Proportionalzirkel oder der britische Sector kann es in Verbindung mit einem Zirkel zum Messen und Konstruieren dienen, es verfügt aber zusätzlich über Sinus- und Tangensskalen und eine logarithmische Skala. Weder Längen noch Winkel können jedoch direkt von einer der Skalen auf Papier übertragen werden, es muss durchgängig ein Zirkel verwendet werden. Insofern ähnelt das Werkzeug dem normalerweise 24 englischen Zoll langen Gunterlineal, das zwischen 1700 und 1900 zur Navigation auf See eingesetzt wurde.

Das Lineal arbeitet mit zwei verschiedenen Längenmaßeinheiten. Die Aufschrift 1 S.H. Fuss interpretiere ich als "Schleswig-Holsteinischer Fuß". Für Schleswig und Holstein (und auch Hamburg) galten seit 1585 gemeinsame Maßeinheiten, das Fußmaß war nach heutigen Einheiten 286,6 mm. 1 Dän. Fuss ist dagegen als "Dänischer Fuß" zu lesen. In Dänemark galt seit 1698 der "Rheinländische Fuß" zu 313,8 mm. Im Jahre 1868 wurden Schleswig und Hostein als preußische Provinz vereinigt. Etwa gleichzeitig wurde im Norddeutschen Bund das im Frankreich 1799 eingeführte metrische System eingeführt, aber noch längst nicht sofort und überall benutzt.  Dennoch wäre es sinnvoll gewesen, es auch mit einer Zentimeterskala auszustatten. Auf den zahlreichen in diesen Jahren neu erschienenen Rechenschiebern ist sie durchgängig vorhanden. Die Herstellung dieses Lineals lässt sich also auf die Mitte des 19. Jahrhunderts oder früher datieren.

Die Ausführung der Teilungen (sehr exakte Raster ohne einzelne Überlängen, erkennbar handgeritzte, aber regelmäßige Skalenstriche, präzise positioniert eingeschlagene Ziffern und zahlreiche zum Schutz der Skalen mit Metallstiften markierten Punkte) ist aufwendig. Sie entspricht der Machart handwerklich gefertigter Zollstöcke, Gunterlineale und Rechenschieber im England des 17. bis 19. Jahrhunderts, insbesondere die Raster und Ziffern wirken aber maschinell positioniert. Das Material ist nicht Buchsbaum, das in England damals bevorzugt benutzt wurde, sondern ein härteres, asthaltigeres Holz, vielleicht Kirschbaum- oder Lindenholz. Leider ist es am linken Ende verzogen und gerissen.

Ergänzende Informationen oder Abbildungen von Geräten mit ähnlichem Skalenlayout nehme ich gern entgegen.

Das Lineal bietet zahlreiche Konstruktionshilfen

Vorderseite:

(Anklicken für größeres Bild)

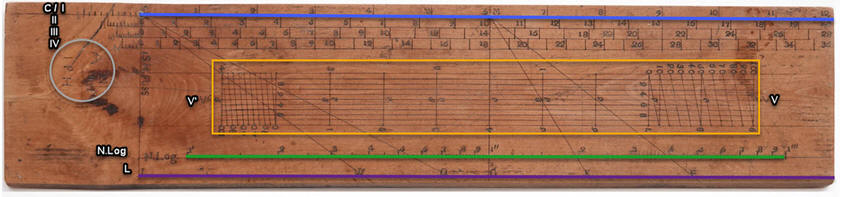
Die abgeschrägte Kante des Lineals (hier als Unterkante) trägt selbst keine Skala und dient nur zum Zeichnen gerader Linien. Streckenlängen müssen mit einem Zirkel von einer Skala zur Zeichnung oder zurück übertragen werden.

Die Maßskala I, benannt mit C (von mir blau markiert), ist 1 S.H. Fuss lang d.h. ein schleswig-holsteinischer oder auch Hamburger Fuß zu 287 mm. Sie ist geteilt in 12 Zoll mit Dezimalen auf der Verlängerung. Dazu gehören die Skalen II mit 20 Teilungen, III mit 28 Teilungen und IV mit 36 Teilungen. Mittels dieser Zusatzskalen kann die Hauptskala auch auf Drittel oder Siebentel Zoll genau abgegriffen werden.

Die Transversal-Skala, benannt mit V bzw V' (von mir gelb umrandet), ist vorwärts von 0 bis 9, rückwärts von 0 bis 3 beziffert und auf Hundertstel genau abgreifbar. Ihre Einheiten sind nicht wie sonst üblich mit Zoll kompatibel, weder mit dänischen noch schleswig-holsteinischen Zoll. Wenn sie nur zum zeichnerischen Addition und Subtraktion von Streckenlängen dienen, ist das auch nicht erforderlich. Transversalmaßstäbe gab es schon seit dem Mittelalter.

Die logarithmische Skala (Gunter's Scale) über zwei Dekaden, benannt N.Log (von mir rot markiert), dient zur Multiplikation und Division. Sie wurde erstmals 1624 von Edmund Gunter nach den Logarithmentabellen von Napier konstruiert und auf dem "Sector" und später dem "Gunter Rule" mit Sinus- und Tangensskalen kombiniert.

Am unteren Rand  (von mir lila markiert) befinden sich auf einer Linie L die Markierungen W, Q, G, K, E. Verbindungslinien mit der Markierung C bzw. M auf der gegenüberliegenden Seite bilden Winkel von 53 und 62 bzw. 30 und 50 Grad zur Null- bzw. Mittellinie der Skala. Ihre Verwendung ist unklar.

Der kleine Kreis (von mir grau markiert) ist mit 43 Punkten markiert. Er ist beziffert mit dem Kürzel I.P.H., den Buchstaben A und N und der Zahl 837. Ob es sich dabei um eine Konstruktionshilfe oder lediglich um eine Herstellermarkierung mit Seriennummer handelt, muss offen bleiben.

Rückseite:

Während viele Elemente der Vorderseite von anderen Zeichenwerkzeugen oder aus der Literatur (Leupold, Bion, Scheffelt) bekannt sind, ist die Rückseite des Werkzeugs sehr ungewöhnlich gestaltet:

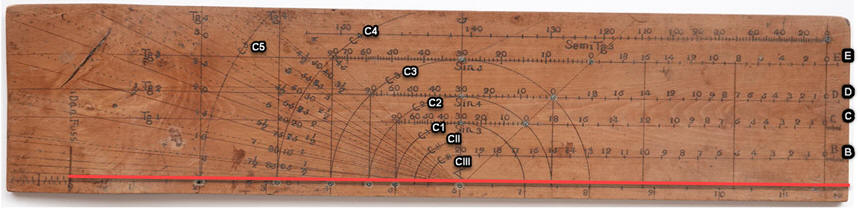
Die Maßskala (von mir rot markiert) ist hier einen dänischen Fuß (314 mm) lang. Sie ist aufgeteilt in 12 Zoll, wahlweise auf Zehntel oder Zwölftel Zoll genau abgreifbar.

Über ihrem Mittelpunkt befinden sich sieben Halbkreise um den Punkt A, benannt vom größten zum kleinsten mit C5, C4, C3, C2, C1, CII, CIII. Darüber als Tangente zu einem kleineren und Sekante zu einem größeren Kreis drei Sinusskalen Sin3, Sin4 und Sin5, die sich nicht auf die jeweils angrenzenden Kreisem sondern auf die "Einheitskreise" C3, C4 und C5 beziehen, außerdem am oberen Rand eine Tangensskala, die sich auf den Kreis C3 bezieht. Der Radius von C1 ist 1 Zoll. Die Radien der Kreise stehen von innen nach außen jeweils im Verhältnis 1:√2, d.h. jeder Kreis hat die halbe Fläche des nächstgrößeren. Zur Durchführung von trigonometrischen Berechnungen wird ein passender Sinus abgegriffen und mittels der Logarithmusskala im Verhältnis des aktuell gegebenen Radius zum jeweils verwendeten "Einheitsradius" vergrößert oder verkleinert.

Die oberste Skala der Rückseite beginnt rechts und ist beziffert mit Semi Tg3. Der Abstand zwischen 0 und 90 auf dieser Skala entspricht dem Radius von C3, also dem Tangens von 45°. Der "Halbtangens" wurde in der sphärischen Trigonometrie verwendet.

Darunter sind vom rechten Rand des Lineals bis an den Rand der Halbkreise vier Skalen E, D, C und B aufgetragen. Sie sind linear in Einheiten beziffert, die sich wie 5:6:7:8 verhalten. Mir ist unklar, welche Beziehung zwischen den Skalen und den Kreisen existiert.

Eine Winkelskala von 0 bis 180, wie sie auch damals meist entlang eines Halbkreises (Transporteur) oder auf drei Kanten eines Rechtecks (Protractor) aufgetragen war, fehlt hier. Stattdessen existiert von M ausgehend über einem Kreisausschnitt von 45 Grad ein Fächer von Linien, auf die man eine Kante oder einen Faden auflegen kann. Die Bezifferungen siind entlang Kreis C4  in Schritten von 5° von 0 bis 45° und in Schritten von 1/2" von 0" bis 4" (nautischen Strichen) und rückwärts von 45° bis 90° und von 4" bis 8" aufgetragen. Eine weitere Winkelskala benannt mit K in Fünf-Grad-Schritten findet sich auf der Tangente an C4.

Konstruktion eines Winkels

1. Greife auf dem Lineal mit einem Zirkel den Radius eines der Kreise C3, C4 oder C5 ab.

2. Zeichne einen Kreis mit diesem Radius um den gewünschten Scheitelpunkt des Winkels.

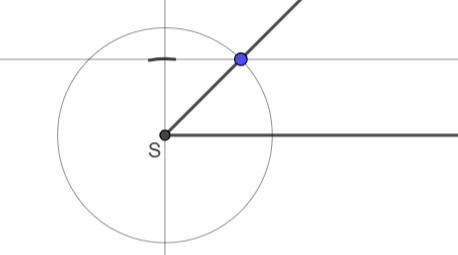
3. Zeichne vom Scheitelpunkt S nach außen eine Halbgerade. Sie bildet den ersten Schenkel des Winkels.

4. Zeichne durch S außerdem eine Senkrechte zu diesem Schenkel.

5. Greife auf der Skala Sin3, Sin4 oder Sin5 passend zum oben gewählten Kreis die Strecke von 0 bis zur gewünschten Gradzahl ab.

6. Markiere diese Gradzahl auf der Senkrechten.

7. Zeichne durch die Markierung eine Parallele zum ersten Schenkel. Die Parallele schneidet den Kreis.

8. Verbinde den Scheitelpunkt S mit diesem Schnittpunkt.

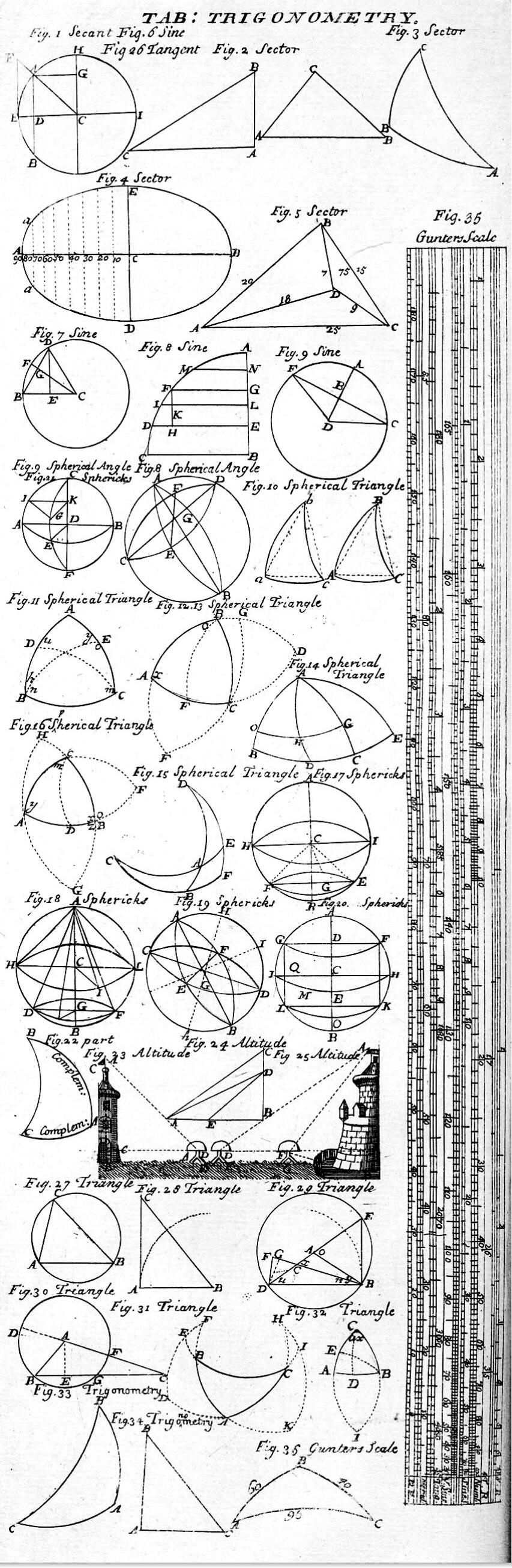
Konstruktionsbeispiele für das Gunter-Lineal (aus Cyclopedia (Chambers) - Volume 2 : Ephraim Chambers 1728 : Internet Archive):

 

Rechenwerkzeug.de