Analog rechnende Geräte
|
Technische Systeme funktionieren heute meist im Dreischritt "Messen - Rechnen - Steuern". Sensoren messen einen Zustand, Computer verarbeiten die von den Sensoren gelieferten Daten und Motoren verändern den Ist-Zustand in der gewünschten Weise. Die Daten sind häufig analog, sie müssen also zunächst einmal digitalisiert werden, bevor sie verarbeitet werden können. Und die digital vorliegenden Resultate des Computers müssen wiederum oft einem analog funktionierenden Regler übergeben werden, um den erforderlichen Kraftaufwand sensibel zu steuern. Früher, als das numerische Rechen noch viel Zeit erforderte, versuchte man dagegen, Rechenvorgänge nur einmal durchzuführen oder ganz zu vermeiden und analoge Ausgangsgrößen analog anzuzeigen oder direkt zu verknüpfen und in andere analoge Größen zu übersetzen. Was der Unterschied zwischen analogen und digitalen Rechnern ist, erfahren Sie in diesem ►Video. Einen Überblick über analog rechnende Geräte liefert Wilfried de Beauclair in ►Mathematik ohne Ziffern. Einen Vergleich der Vorzüge analoger und digitaler Rechenverfahren gibt Andreas Brennecke im ►Rechnerlexikon. Eine Sammlung elektronischer Analogrechner zeigt Bernd Ulman im ►Analogmuseum. Hinweise auf online einsehbare Literatur findet sich ►hier und ►hier und ►hier. |
|
|
Nach einer von mehreren Theorien diente die etwa 4000 Jahre alte
►Himmelsscheibe von
Nebra als analoger Kalender: "Die Horizontbögen überstreichen jeweils einen Winkel von 82 Grad, ebenso wie
Sonnenauf- und -untergang zwischen Winter- und Sommersonnenwende am
Horizont auf dem Breitengrad des Fundorts. Wurde die Scheibe waagerecht
so auf dem Mittelberg positioniert, dass die gedachte Linie vom oberen
Ende des linken Bogens zum unteren Ende des rechten Bogens auf die
Spitze des etwa 85 km entfernten Brocken zeigt, konnte die Scheibe als
Kalender zur Verfolgung des Sonnenjahrs genutzt werden." (Text und Grafik: wikipedia) |
 |
|
Der älteste bekannte mechanische Analogrechner stammt aus dem 2. Jahrhundert vor
Christus. Es ist der ►Mechanismus von Antikythera, der
das Sonnensystem nachbildete und z. B. die Vorhersage von Sonnen- und
Modfinsternissen erlaubte. Das Wissen über astronomische Zusammenhänge ging in der Folgezeit verloren. Erst im 16. und 17. Jahrhundert bauten Astronomen wie Wilhelm Schickard und Philipp Matthäus Hahn, wieder Himmelsgloben und Weltmaschinen mechanische Weltmodelle. (Foto: Ausschnitt aus der Weltmaschine im Landesmuseum Darmstadt) |
 |
| Von Philipp Matthäus Hahn stammt auch diese Neigungswaage. Auf der linken Seite, am Zeigerarm ist ein Gewicht befestigt, an einer von mehreren Positionen des Hebels das zu wiegende Objekt. Mit der Neigung des Arms bewegt sich der Zeiger. Das Gewicht des Gegenstands kann auf der zum Befestigungsabstand korrespondierenden Skala abgelesen werden. (Foto: Hahn-Museum Onstmettingen) |
 |
|
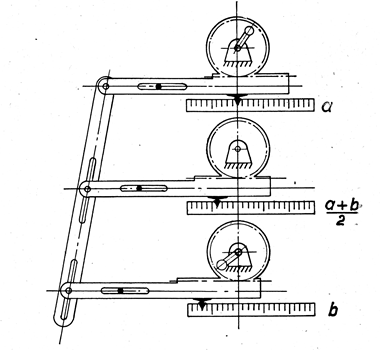
Hans Körnwien skizziert in seinem Buch
►"Graphisches Rechnen"
von 1949 auf Seite 259 ein einfaches Gestänge, mit dem man drei Zeiger (oder
Regler) in
ein festes Verhältnis zueinander setzen kann. Im Beispiel wird auf drei gleichen
linearen Skalen aus den beliebig einstellbaren Zahlen a und b das
arithmetische Mittel gebildet. Durch die Verwendung unterschiedlicher Skalenweite (Zahnradgröße) oder den (teilweisen) Einsatz logarithmischer Skalen ist dieses System vielfältig variierbar. |
 |
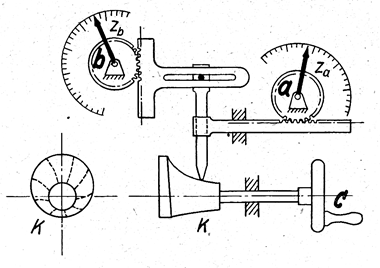
| Im Lehrbuch ►"Graphisches Rechnen" von Hans Körwien findet sich auf Seite 261 auch die Skizze einer Vorrichtung, mit der den beiden Anzeigen (oder Reglern) a und b ein festes Produkt c zugeordnet werden kann. Ändert sich a, so passt sich b an und umgekehrt, aber das Produkt bleibt erhalten. Durch Einstellung einer Kurbel c kann das gewünschte Produkt verändert werden. Der Körper K ist so geformt, dass die Hyperbeln einer Hyperbeltafel mit allen Zwischenwerten stufenlos darauf abgegriffen werden können. |
 |
|
Der Schnellkalkulator System Bloch ist ein
mechanisches Nomogramm mit 7 logarithmischen Skalen über zwei
miteinander verbundenen Hebeln und einem drehbaren Flügel. Er dient zur Kalkulation von Akkordzeiten für Dreh-, Bohr-, Fräs- oder Hobelarbeiten an spanabhebenden Maschinen. Das Gerät liefert nach Einstellung von Länge und Breite oder Durchmesser eines Werkstücks, der Umdrehungsgeschwindigkeit und dem Vorschub pro Umdrehung der Maschine die Bearbeitungszeit in Minuten. ►Animation (Schnellkalkulator) Zu diesem Analogrechner existiert eine Abwandlung, mit der man das Volumen und Gewicht der erzeugten Fräs- und Drehteilen bestimmen kann. ►Animation (Gewicht-Schnellrechner) |
 |
|
Kompliziert geht es im Inneren des Stabilogauge zu. Das ist ein
analoger
Schiffsstabilitätsrechner. Die Nutzlasten 'Deck Load', 'Upper 'Tween
Deck', 'Lower 'Tween Deck', 'Nos 1-4 Holds & Deep Tanks' und 'Double
Bottom Tanks' und die 'Density Correction und 'Free Surface
Correction' werden über Mikormeterschrauben eingegeben. Deadweight
(tons)', 'Displacement (tons)' und 'Mean Draft (feet)' werden auf
der horizontalen Skala abgelesen und 'GM' (Metazentrische Höhe) auf
der vertikalen Skala. Verschwindet der GM-Zeiger unter der roten
Flagge, ist das Schiff instabil. Die Position der roten Flagge ist
nicht konstant. Sie hängt ab von allen
Mikrometerschraubeinstellungen. Wenn die rote Flagge im GM-Fenster
sichtbar ist, ist das Schiff im Schadensfall möglicherweise nicht
stabil genug." (Text und Bild: Andries de Man im Rechnerlexikon) |
 |
|
Ein Gerät nach anderem Prinzip, aber mit ähnlicher Funktion ist Eriksberg's Loading Guide nach dem
System von Thorsten Andersson. Es wurde 1954 speziell für den Tanker ►T/T
Tarim entworfen. Bei Frachtschiffen ist es wichtig, die Ladung gleichmäßig in die Laderäume zu verteilen. Hängt der Bug oder das Heck zu tief, so ist das Schiff schwer zu steuern. Konzentriert sich die Ladung auf die Mitte (Sagging) oder die beiden Enden (Hogging), so verzieht sich der Schiffsrumpf und wird bei Seegang starken Belastungen ausgesetzt. Mit diesem analogen Addierer kann man die Ladung eines Frachtschiffes vor dem Beladen so über die Länge des Schiffes verteilen, dass das Schiff horizontal im Wasser liegt (Trimmen) und der Rumpf gleichmäßig belastet wird (Stress). Außerdem kann der aus dem Gesamtgewicht der Ladung resultierende Tiefgang ermittelt werden. Wo die in Fuß angegebene Trimmzahl (Neigung des Schiffsrumpfs) gemessen wird, wie sie ausgeglichen werden kann und wie die Spannung in die grafisch angegebenen Toleranzgrenzen gebracht wird, ist der beigefügten Anleitung nicht zu entnehmen. ►http://rechnerlexikon.de/artikel/Eriksbergs_Loading_Guide ►Animation ►Excel-Version (Bild: W. Schumann) |
 |
|
Mechanische Zahlenrechner arbeiten in der Regel digital. Nachdem das
Einerzahnrad eine volle Umdrehung von 1 bis 9 zurückgelegt hat, wird
beim Übergang von der 9 zur 0 das Zehnerrad um eine Stelle
mitgenommen. Mechanische Ungenauigkeiten werden durch
Raststellungen eliminiert. Man kann sich aber auch die Rasten sparen und dem Benutzer den Rundungsvorgang überlassen, Je nachdem, wo man beim IFACH-Addierer einsticht wird bei der Drehbewegung die Scheibe so positioniert, dass im Ergebnisfenster eins von zwei möglichen Ergebnissen den Vorrange erhält. |
 |
| Ein anderes Beispiel ist das Addierwerk der Maschine von Tschebyschew, die auf einem Planetengetriebe mit Übersetzungen von jeweils 10:1 basiert. Die Ziffer, auf die der Zeiger in der Einerstelle zeigt, bestimmt die Position des Zeigers über der Zehnerstelle. |
 |
|
Der Stellenübergang muss nicht dem Zehnersystem folgen: Komplizierter wird es, wenn die Übersetzung veränderbar
sein soll wie beim Rechenwerk einer Zapfsäule.
Das untere der beiden großen Zählwerke läuft analog mit der Pumpe und zeigt die
getankte Benzinmenge an, das obere zeigt den zu zahlenden Preis. Über
jedem der beiden großen Zählwerke befindet sich ein kleines grünes
Zählwerk, das die insgesamt getankte Menge bzw. die gesamte Einnahme
anzeigt. Die kleinste Stelle läuft jeweils stufenlos, die Zählwerke
selbst aber funktionieren mit digitalem Zehnerübergang. Mithilfe der drei Zahlenwalzen am unteren Rand kann der Tankwart den Preis pro Liter verändern. Während die einzelnen Stellen beider Zählwerke dem Dezimalsystem folgen, geschieht die Kopplung von Menge und Preis über ein einstellbares fein gestuftes Schaltgetriebe. Für die variable Übersetzung zweier Drehzahlen gibt es aber auch komplett stufenlos einstellbare Lösungen, so etwa das ►DAF Variomatic Getriebe für Autos oder das ►nuVinci-Getriebe für Fahrräder. 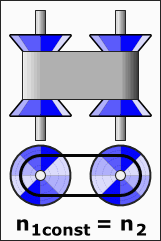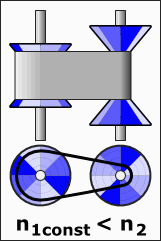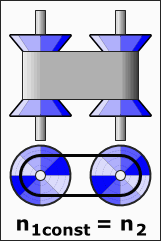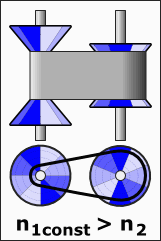 |
  |
|
Getriebeübersetzungen kann man zum Zahlenrechnen benutzen. Hier ein Getrieberechner von Leonardo Torres Quevedo (1895) zur Bestimmung der reellen und komplexen Lösungen kubischer Gleichungen. Eine Räderwerk zur mechanischen Berechnung von Funktionstabellen hatte bereits Charles Babbage ab 1822 entwickelt, aber mangels finanzieller Unterstützung durch den Staat nur als Funktionsmodell fertigstellen können. Die "Differenzmaschine" funktioniert jedoch nicht analog, sondern digital, denn sie besteht aus einer Kombination von Zählwerken, die sprungweise laufen.
|
|
| Dieser Universal-Gleichungslöser für Polynome 3. Grades wurde bereits von Leibniz erdacht und von Janos Segner (1704-1777) in der Enzyklopädie von Diderot und d'Alembert als Entwurf veröffentlicht, aber erst im 20. Jahrhundert tatsächlich gebaut. ►Näheres ►Website |
|
|
Bei einem mechanischen Tachometer wird die Umdrehung des Rades mit einem Haken abgegriffen und mit
einer Welle zum Tacho übertragen. Dieser rechnet über ein kleines
Getriebe die Anzahl der Radumdrehungen in Kilometer um und gibt sie
auf ein Zählwerk. Eine Metallglocke dreht sich dabei gleichzeitig um einen an der Tachonadelachse befestigten Dauermagneten und erzeugt dabei magnetische Wirbelströme. Abhängig von der Drehzahl wird die Achse gegen eine Feder unterschiedlich stark mitgenommen. Der Zeiger des Tachos bewegt sich dabei über eine Skala (UpM / km/h). Die Funktion Zeit -> Geschwindigkeit (Tachonadel) ist die erste Ableitung der Funktion Zeit -> Weg (Kilometerzähler). |
 |
|
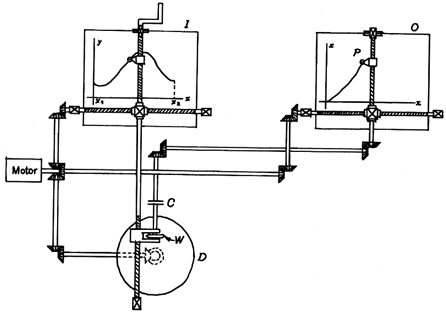
Umgekehrt ließe sich aus der
Funktion Zeit -> Geschwindigkeit die Funktion Zeit -> Weg gewinnen.
Hierzu benötigt man einen "Reibradintegrierer" Auf
einer Integrierscheibe D dreht sich eine Rolle W. Diese wird bei hoher
Geschwindigkeit an den äußeren Rand der Scheibe geführt und dreht sich
dort entsprechend schneller als weiter innen. (Abbildung aus: Karplus,
Soroka: Analog Methods - Computation and Simulation. New York 1958) |
 |
|
Ein analoger Integralrechner, mit dem man Flächeninhalte messen kann. Der Rand
einer Figur
wird mit einem Stift umfahren. Dabei registriert eine mitlaufende Rolle
die Dreh- und Schubbewegungen des Fahrarms. Während die Drehbewegungen
sich in der Summe gegenseitig aufheben, ergibt die Summe der Schubbewegungen
ein Maß für den Flächeninhalt der umfahrenen Figur. Dieser kann auf
drei bis vier Stellen genau abgelesen werden. ►Wie funktioniert ein Planimeter |
 |
|
Eine Maschine zur Berechnung von Gezeiten von 1920. Die
rückseitige Beschriftung der Postkarte lautet: "Uncle Sams mechanischer
Prophet.". Auf der Aufnahme von der Rückseite kann man all die kleinen
Räder erkennen, die zusammenarbeiten um die Zahlenfülle einer
Gezeitentabelle zu erzeugen, die von den Küstenbehörden und geodätischen
Ämtern in Washington veröffentlicht werden. Das Gerät berücksichtigt
gleichzeitig 37 Einflussfaktoren, darunter die relative Position von
Sonne, Mond und Erde und die Form des Hafens. Es berechnet die Zeit und
Höhe des Hoch- und Niedrigwassers für hunderte von Häfen. Die interne
Toleranz der Maschine beträgt 1/600 Zoll. |
|
|
Das 19. und das frühe 20. Jahrhundert waren die große Zeit analoger Mess- und Steuerungssysteme.
Fliehkraftregler steuerten die
gleichmäßige Kraftabgabe von Dampfmaschinen und Wasser-kraftwerken.
Bordrechner halfen bei der Last-verteilung, Kreiselkompasse
bei der Steuerung von Schiffen. Mechanische Analogrechner
halfen als Feuerleitsysteme, um bereits beim
Abschuss von Torpedos die Bewegung des feuernden Schiffes und des
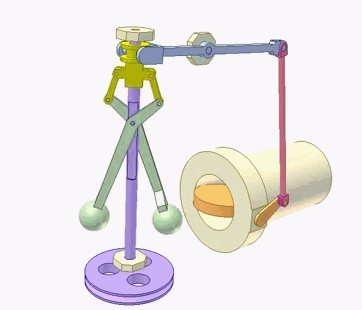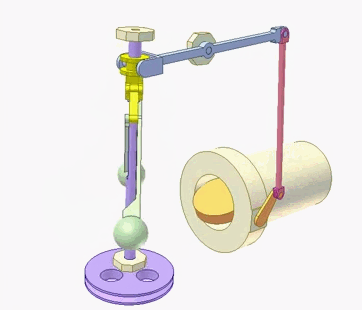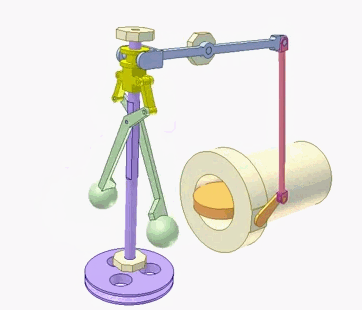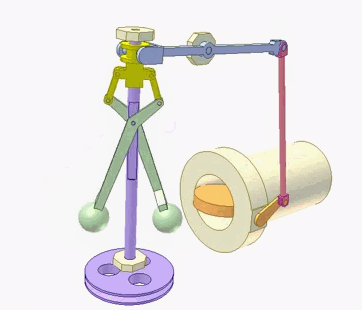
Ziels zu berücksichtigen. Zur Steuerung und Stabilisierung von Raketen wurden die Signale der Messeinrichtungen mittels elektronischer Analogrechner summiert, multipliziert oder integriert. Digitalrechner wären viel zu langsam gewesen. Hier ein früher ►Analogrechner zur Flugsimulation |
 |
| Der MONIAC (Monetary National Income Analogue Computer), auch bekannt als Phillips Hydraulic Computer oder Financephalograph ist ein Analogcomputer, der mittels Wasserflüssen (Fluidik) den Geldfluss durch eine Volkswirtschaft simuliert. Der Computer wurde 1949 vom neuseeländischen Ökonomen und Erfinder Alban W. Phillips entworfen und zusammengebaut, während Phillips noch Student der London School of Economics (LSE) war. Etwa vierzehn Exemplare des MONIAC wurden gebaut. Der MONIAC konnte komplexe Berechnungen vornehmen, die von anderen Computern dieser Zeit nicht verarbeitet werden konnten. Verschiedene Wassertanks simulierten Haushalte, Wirtschaft, Staat, Export und Import. (Wikipedia) |
 |
|
Ein
einfacher
elektronischer Analogrechner ist der Edmund Analog Computer.
Damit können numerische Multiplikationen und Divisionen
(mithiilfe der Skalen auch von Sinus-, Kosinus- und Tangenswerten gegebener Winkel) durchgeführt werden. Man stellt mit dem linken Drehknopf den ersten Faktor ein, der mittlere
Drehknopf wird auf den zweiten Faktor gestellt und der rechte Drehknopf solange
gedreht bis bei gedrücktem Testknopf auf der Anzeige die Nullstellung erreicht
ist. Dann kann auf der rechten Skala das Ergebnis abgelesen werden. Das Ganze funktioniert wie eine Potentiometerschaltung mit drei Potis und
wird von zwei 1,5-Volt-Batterien gespeist. Die Zeiger
an den Potis können zur Eichung und Verbesserung der Genauigkeit mit
Madenschrauben verstellt werden. |
|
|
Während das vorhergehende Gerät als Bausatz für Bastler auf den Markt kam, war das nebenstehend abgebildete Gerät offenbar ernsthaft als analoger Taschenrechner gedacht. Der MATH-O-MATIC Star-lite NOMT- 660 wurde etwa in den 60er Jahren (also noch vor den digitalen Taschenrechnern) in Japan hergestellt. Er ist etwa 15cm x10cmx4cm groß. Wer ihn kaufte und wozu er eingesetzt wurde, bleibt im Dunkeln. Ausweislich seines Einstellrads beherrschte er Multiplikation, Division Prozentrechnung und sogar Quadrieren und Wurzelziehen. Photo courtesy of Professor Mohamad H. Hassoun, Detroit, Michigan, USA
|
|
|
In der ersten Hälfte des 20. Jahrhunderts gab es sogar etliche elektronische
Analogcomputer. Nachdem sie in den 1970-er Jahren
fast ausgestorben waren, werden heute wieder neue Varianten entwickelt und mit Digitalrechnern zu
Hybridsystemen kombiniert. Dies ist "The Analog Thing", ein Lerncomputer. Er enthält analoge elektronische Bauelemente (Potentiometer, Summierer, Inverter, Multiplizierer und Integrierer), die man durch individuelle Kombination dazu bringen kann, Spannungsverläufe zu erzeugen und vorgegebene Abläufe zu simulieren. Das erfolgt Real Time: Messwerte werden dabei nicht in Zahlen übersetzt und es gibt keinen Algorithmus, der im Speicher abgelegt und von einem Prozessor schrittweise abgearbeitet wird. Ein- und Ausgabe erfolgen durch Übergabe von Signalen im Bereich zwischen -1 Volt und 1 Volt. Die Ziffernanzeige des Geräts dient zur zur Einstellung der acht Potentiometer und zur Anzeige der Spannung an beliebigen Punkten der Schaltung. Signalverläufe lassen sich mit einem Oszilloskop anzeigen. Das Gerät enthält vier Addierer, zwei Multiplizierer, fünf Integrierer und zwei Vergleicher. |
 |
Rechenwerkzeug.de
