Zählhilfen, Rechenbretter und Abakusse
|
"Die Behandlung von Zahlen, das Rechnen und die Mathematik sind nicht denkbar ohne spezifische „Werkzeuge", es sei denn, alle Operationen spielten sich ausschließlich im menschlichen Gehirn ab. Speicherkapazität wie auch Umfang und Geschwindigkeit der Verknüpfung sind jedoch begrenzt, deshalb sah sich der Mensch frühzeitig genötigt, Entbehrliches auszulagern und für das Speichern und Operieren entsprechende Hilfsmittel einzusetzen. Noch bevor dazu schriftliche Symbole - also ►Zeichen für Zahlen und Operationen - vereinbart wurden, versuchte man sich zunächst mit einer gegenständlichen Darstellung. Das Material dafür lieferte die Natur: die Körperteile des Menschen (vor allem Finger und Zehen) sowie Steine, ►Knochen, Stäbchen, Muscheln, harte Früchte oder zu ►Schnüren gebundene Fasern. So leiten sich beispielsweise vom „kleinen Kieselstein", dem lateinischen calculus, die Worte Kalkül, kalkulieren und Kalkulator (engl. calculator) ab." (Friedrich Naumann "Vom Abakus zum Internet", S. 27) Schon auf einer
Vase mit Bildern des Perserkönigs Darius um 500 v. Chr. rechnet ein Beamter mit
Zahlsteinchen auf einem Rechentisch. Aus dieser Zeit stammt auch das älteste erhaltene
Rechenbrett, die
►Salaminische
Tafel. Die Römer entwickelten ihr Rechenbrett weiter zum
Handabakus, der in Spalten verschiebbare Perlen für Einer, Fünfer,
Zehner usw. enthielt. Dieses Gerät tauchte auch um 1300 in China
auf. Im Rest der damaligen Welt überlebte der Rechentisch das
Mittelalter. Daneben lehrte der deutsche Rechenmeister Adam Riese
alternativ auch die schriftlichen Rechenverfahren, die zusammen mit
den indischen Ziffersymbolen einschließlich der Null über die Araber
zu uns gelangt waren.
►Rechnen
mit dem Abakus |
||
|
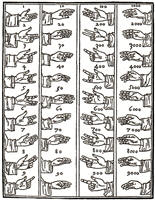
Zahlcodes mit Fingern Beda Venerabilis um 725 Einer und Zehner mit linker, Hunderter und Tausender mit rechter Hand |
Beim englischen Benediktinermönch Beda Venerabilis (um 725) findet
sich dazu die eine Beschreibung, wie man mit dem Beugen und
Auifrichten von kleinem Finger , Ringfinger und Mittelfinger der
linken Hand die Ziffern 1 bis 9 und mit Daumen und Zeigefinger die
Zehner von 10 bis 90 darstellen kann. Die rechte Hand kommt
entsprechend bei den Hundertern und Tausendern zum Einsatz.
Verwendet wurde das System zum Zählen, zum Merken und als
Zeichensprache. |
 |
Abakus als Zählgerät Alter unbekannt Herkunft unbekannt |
Dieser Abakus mit 20 verschiedenfarbigen Kugeln ist auf den seitlichen Leisten mit Tier- und Jagdmotiven bemalt. Dies könnte auf den Inhalt des Spiels hindeuten. Denkbar wäre, dass auf der unteren Leiste die Gesamtzahl der Spiele und auf den beiden kurzen Leisten die Zahl der gewonnenen Spiele zweier Spieler mitgezählt wurden. |

|
Bezique Marker Charles Godall & Sons Camden, London ab 1890 Großhandelspreis: 9 Schilling für 12 Gerätepaare |
Addiergerät mit 4 Stellen nach dem Prinzip des Abakus Beim Bézique-Spiel aus Frankreich (in Deutschland als Binokel bekannt) gibt es Punkte für bestimmte Kartenkombinationen. Diese werden mit dem Marker addiert. Das spielkartengroße Gerät funktioniert wie ein vierstelliger Abakus mit Einer- und Fünferkugeln. Sein Clou ist der verborgen eingebaute Federmechanismus für die Klappen. |

|
Römisches Rechenbrett (nach einer Reproduktion im Römerkastell Saalburg) Nachbau 2002 R.A. |
Die Spaltenbezeichnungen stehen von links nach rechts für Millionen,
Hunderttausender, Zehntausender, Tausender, Hunderter, Zehner, Einer
und Zwölftel. Der obere Teil des Rechenbretts ist genauso aufgebaut wie der römische Handabakus. Allerdings fehlt die Spalte für die kleinsten Münzen. Die untere Felderzeile wurde beim Multiplizieren für den Multiplikator verwendet. |
 |
Römischer Handabakus Nachbildung nach einem Original in der Bibliotheque Nationale in Paris Anfertigung 2017 Replik.de Download: Römischer Taschenrechner für Windows |
Sieben dezimale Spalten für Millionen, Hunderttausender,
Zehntausender, Tausender, Hunderter, Zehner und Einer.
Die Perlen unten zählen jeweils einfach, die oberen fünffach. Die Einer (Zeichen I, dritte Spalte von rechts) sind in Zwölftel aufgeteilt (Zeichen Θ, unten fünf Einer- und oben eine Sechserperle). Mit der Spalte ganz rechts kann man diese Zwölftel weiter halbieren, dritteln oder vierteln. ►How did the Romans calculate ►Calculating with roman Numbers |

|
Rechenbrett nach Gerbert von Aurillac 950-1003 Nachbau 2021 R.A. |
Während damals in Mitteleuropa weiter mit dem System der Römischen
Zahlen gerechnet wurde, verwendete der Mönch, Astronom und
Mathematiker Gerbert (Berater der deutschen Kaiser Otto II und Otto
III und später Papst Sivester II) bereits die arabischen Zahlen, die
er bei seinen Studien in Andalusien kennengelernt hatte. Weil er die
Null noch nicht kannte, mussten er die Ziffernsymbole auf einem
Rechenbrett anordnen. Seine mathematischen Texte sind in der
Sammlung
►Geometria
überliefert. ►Näheres ►Rechenbeispiel |
 |
Rechenkamm nach Johannes de Elsa Bordeaux um 1310 Nachbau 2022 R.A. ►Historia Mathematica |
In einer mittelalterlichen Handschrift fand
Menso Folkerts die Beschreinung eines ungewöhnlichen Rechenbretts:
eine Art Kamm aus Blei den man man als
Hilfe sowohl für das Rechnen mit ganzen Zahlen
als auch mit
Sechzigstelbrüchen oder Münzen
verwenden konnte. Der Rechenpfennig auf der vertikalen Leiste
besitzt, sofern vorhanden, den fünffachen Wert der Rechenpfennige auf
dem jeweiligen Zinken. Im Falle von Bruch- und Münzrechnung werden
auch die Zwischenräume als nichtdezimale "Zwischen-Stellenwerte" einbezogen. Näheres |
|
|
Rechenbrett
nach Adam Riese 1492-1559 Nachbau 2000 R. A. ►Virtueller Rechentisch |
Plättchen auf den Linien repräsentieren von unten nach oben Einer, Zehner
Hunderter, Tausender. Plättchen dazwischen stehen für Fünfer, Fünfziger,
Fünfhunderter. Das Rechenbrett konnte auch ein mit Linien besticktes
Tuch oder ein mit Intarsien furnierter Tisch sein. Gerechnet wurde mit
speziellen Münzen ohne Geldwert, so genannten Rechenpfennigen. ►Tino Hempel |
|
|
Rechenpfennige aus Kupfer und Bronze Deutschland 1485, 1596, 1667 und 1753 Ø ca. 3 cm, ca. 1 mm dick |
Rechenpfennige waren Münzen, die keinen
Geldwert hatten, wohl aber reichhaltig mit Vignetten und Sprüchen
versehen waren. Gerechnet wurde meist auf einem Tuch oder einem speziellen Tisch, der mit eingelegten
Linien versehen war. Die Methoden zum Rechnen finden sich in
Adam Rieses Rechenbuch |
|
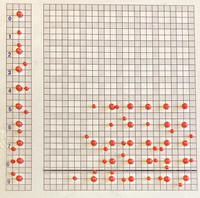
Rechenbrett für Blinde Steckbrett für Ziffernsymbole aus Stecknadelköpfen Nicolaus Saunderson England um 1700 Nachbau R.A. 2021 |
Nicolaus
Saunderson, geboren 1682, war im Alter von einem Jahr
erblindet. Weil er infolge dieser Behinderung weder lesen noch
schreiben konnte, schuf er sich eigene Hilfsmittel für Notizen und
Rechnungen. Auf dem abgebildeten Steckbrett konnte er Diagramme darstellen, Zahlen notieren und sogar rechnen. Im Jahre 1723
wurde er als Lehrer an die Universität Cambridge berufen. Er
veröffentlichete unter anderem eine zweibändige "Abhandlung über die
Algebra". Quelle: Zeitschriftenartikel aus 1841 Weitere Beschreibung in "Versuch einer Geschichte der Rechenmaschine" von Johann Paul Bischoff 1804 |

|
Stschoty russischer Abakus ab ca. 1700 hergestellt ca. 1990 |
12 Stellen Der Stab mit vier Kugeln wurde für Viertelrubel verwendet, die drei Stäbe darunter für Kopeken (Zehner, Einer und Viertel). Häufig finden sich in der untersten Stelle ebenfalls nur vier Kugeln (für Viertelkopeken). Anwender |

|
Deutsche Schulrechenmaschine Taschenausgabe 1962 große Ausgabe IKEA Preis 1995: 20 DM |
10 Stellen Jede Stange repräsentiert eine Dezimalstelle, von unten nach oben: Einer, Zehner, Hunderter, usw. Da in jeder Stelle 10 statt 9 Kugeln vorhanden sind, können Überträge zeitweilig unbereinigt bleiben. Als Napoleons Soldaten auch den Abakus aus Russland nach Westeuropa reimportierten, hatten sich hier die schriftlichen Rechenverfahren so weit durchgesetzt, dass die hölzernen Hilfsmittel hierzulande nur noch als Lehrmittel Verwendung fanden. |

|
Ch'eou chinesisches Rechenbrett Sangi japanisches Rechenbrett Nachbau 2021 R.A. |
Bevor sich um 1300 von China ausgehend der Gebrauch des Suanpan / Soroban durchsetzte wurde dort mit Stäbchen auf Rechenbrettern gerechnet. Allen Varianten gemeinsam war die Verwendung des Dezimalsystems. Die Länge (5-15 cm), Dicke und Material der Stäbchen (Holz, Bambus, Knochen) variierten, ebenso wie die Gestaltung der Fünfersymbole. Negative Zahlen wurden durch Durchstreichen einzelnen Ziffensymbolde mithilfe eines schräg darübergelegten Stäbchens gekennzeichnet. Hier ein Rechenbeispiel |

|
Suanpan chinesischer Abakus hier 9-stellig aus Knochen, öfter 13-stellig aus Holz In dieser Form verbreitet seit dem 14. Jahrhundert, vorher wurden Ziffern meist mit Holzstäbchen in einer Tabelle aus Quadratfeldern dargestellt. |
Wie beim römischen Abakus haben die oberen Perlen jeder Stelle ("Himmel") den fünffachen Wert der unteren Perlen ("Erdel"). Die zweite Kugel oben und die fünfte Kugel unten sind im Dezimal-system überzählig, erleichtern aber den Übertrag. Daneben ist in jeder Stelle die Darstellung der Ziffern 0-15 möglich. Laut "The Abacus Handbook" wurde mit dem Suanpan bisweilen auch hexadezimal gerechnet: Maßeinheiten in China waren früher im 16-er-System aufgebaut. Rechenkünstler ►Wikipedia (engl.) |
|
|
Soroban (Japan) Abwandlung des chinesischen Suanpan vor 1937 |
27 Stellen (auch mit 13, 17 oder 21 Stellen üblich). Die Perlen haben hier die Form von Doppelkegeln. Gegenüber der chinesischen Form des Abakus wurde 1868 die überzählige Fünferperle verboten und um 1937 in Lehrbüchern auch noch die überzählige Einerperle eingespart, sodass in der modernsten Generation der "Himmel" jeder Stelle nur noch eine Perle und die "Erde" nur noch vier Perlen enthält. ►Jörn Lüthjens ►Herstellerwebsite |
|
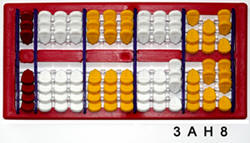
Nepohualtzintzin (auch: Nepoualtzitzin) Maya-Abakus nach David Esparza Hidalgo mit Klappenmechanismus 13-stellig ►Animation ►Vorführung |
Abakus für das
Vigesimalsystem (20-er-System) Stellenwert unten v.r.n.l.: dezimal: 1, 20, 400, ... Stellenwert oben v.r.n.l.: dezimal: 5, 100, 2000, ... Einstellung: 3AH8 vigesimal = 3*8000+10*400+18*20+8 = 28368 dezimal Bei Verwendung als Kalender kann jede Spalte eine Woche repräsentieren: 13 Spalten = 91 Tage = ein Vierteljahr. ►Verwendung ►Theorie ►Abakus-Vergleich ►Didaktik |

|
Yupana Inka-Abakus nach einer Abbildung in Felipe Guaman Poma de Ayala (1535-1616): "El primer nueva corónica" hier fünfstellig dezimal Heute Lehrmittel in Peru Nachbau R.A. 2020 |
Der bei Guaman abgebildete ►Yupana
folgt dem Aufbau der ►Quipu-Knotenschnüre
(dezimale Stellen von unten nach oben wachsend ). Erhaltene Keramiken, die
offenbar als
Yupana verwendet wurdem, besitzen aber einen
recht unterschiedlichen Aufbau und für die Zahldarstellung auf dem
bei Guaman
abgebildeten Yupana existieren mehrere Lesarten (dezimal oder vigesimal oder noch anders? Symbol
auf dem Feld
= Maximalzahl der Zahlsteine oder Wert eines Steins auf dem Feld?). Entsprechend unterschiedlich
wären die Rechenverfahren. ►Raúl Ibánez ►Jim Allen ►Molly Tun ►Aufbau ►Wettrechnen auf Youtube |
Rechenwerkzeug.de