Rechnen mit dem chinesischen Rechenbrett

Die Mathematiker David Eugene Smith und Yoshio Mikami haben im Jahr 1914 die alle zugänglichen Quellen gesichtet und die Geschichte der japanischen Mathematik aufgeschrieben. Das Buch (in Englisch) ist bei archive.org zum Download verfügbar.
Hier einige übersetzte Auszüge aus den Seiten 24 bis 27:

Zahldarstellung

Um das Jahr 1300 kam in China, in Japan, Korea und der Mongolei nach und nach der Abakus (Suanpan, Soroban) als Rechenhilfsmittel in Mode. Vorher hatt man in Ostasien mit Stäbchen auf einem Rechenbrett gerechnet. Die Stäbchen gab es in längeren und kürzeren Varianten, eine Tabelle auf dem Boden diente als Rechenbrett, Zahlenangaben und Rechenergebnisse in Büchern wurden mit den Stäbchen entsprechenden Strichmustern, aber ohne Tabelle geschrieben.

Die Zahldarstellung ähnelt unserer Bierdeckelrechnung. Die Einerstelle wird mit vertikalen Stäbchen gelegt.
Um Fünfer darzustellen, wird kein Schrägstrich gezogen, sondern ein horizontales Stäbchen darübergelegt:

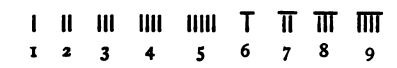
In der Zehnerstelle wird dagegen mit horizontalen Stäbchen begonnen. Ein darunter gelegtes vertikales Stäbchen hat den Wert 50:

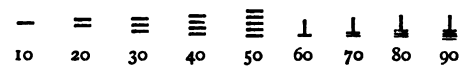
Die Hunderter werden wieder dargestellt wie die Einer, die Tausenderstelle wie die Zehner usw.

Die Zahl 38057 wurde also so gelegt:

und so geschrieben.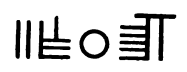

---

Rechenverfahren

Die Rechenverfahren besitzen starke Anklänge an die Art, wie wir auf Papier rechnen. Um auf dem Rechenbrett zwei Zahlen zu addieren, legt man sie in zwei Zeilen stellengerecht untereinander und fasst dann Stelle für Stelle zusammen:
342 + 965 = 1207.

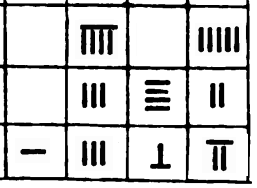
Bei der Division sind etwas mehr Schritte erforderlich: Nehmen wir zum Beispiel die Aufgabe 276 : 12.
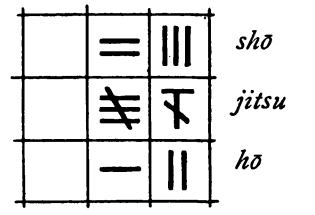
Wir schreiben den Dividenden (jitsu) in die mittlere Zeile und setzen den Divisor (ho) linksbündig darunter.
Die obere Zeile bleibt frei für den Quotienten (sho).

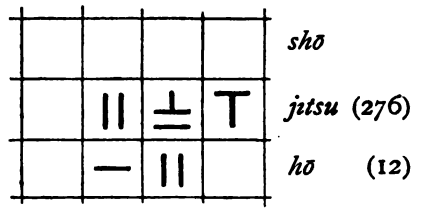
Dann streichen wir die Stelle des Dividenden durch und kennzeichnen ihn so als negativ:

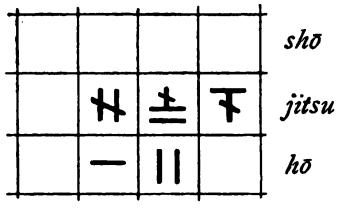
Wir schätzen ab, wie oft der Divisor (12) in den darüber stehenden Stellen des Dividenden (27) enthalten ist und notieren: zwei Mal.

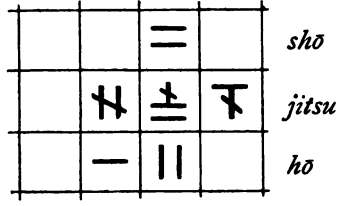
Dann multiplizieren wir den Divisor mit 2 und legen das Ergebnis (24)
neben die beiden als negativ gekennzeichneten  Stellen des Divisors:

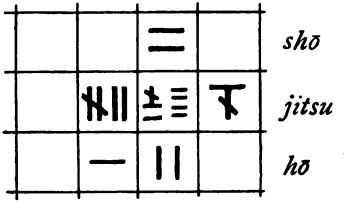
In der Hunderterstelle geht die Rechnung auf, es bleibt nichts übrig, In der Zehnerstelle ergibt die Subtraktion 7 - 4 den Rest 3.
Nun verschieben wir den Divisor um eine Stelle nach rechts.
Wir schätzen ab, dass er im Rest (36) drei Mal enthalten ist und legen die 3 in die Einerstelle des Quotienten.

 Die Mutliplikation 12 mal 3 ergibt genau 36.

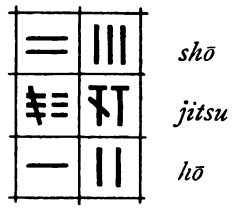
Und die Subtraktion 36 - 36 bleibt ohne Rest.

Ergebnis auf dem Rechenbrett: 23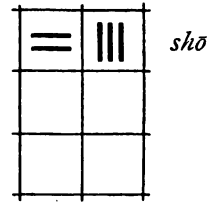

und als Schriftzeichen: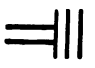

 

Rechenwerkzeug.de