Tabellen, Formeln und Tafelwerke
|
Vor dem Siegeszug von Taschenrechner und Tabellenkalkulation erleichterte man sich das Leben, indem man häufig gebrauchte Zahlenwerte in Form von Formeln und Tabellen zum Nachschlagen bereitstellte. Während etwa das Nachschlagen des kleinen Einmaleins in einer Tabelle einem heutigen Europäer kindlich vorkommt, waren Tabellenhefte noch vor hundert Jahren eine echte Arbeitserleichterung und auch im Arbeitsleben weit verbreitet etwa im Falle von Zinsfaktoren . Tabellen konnten auch beweglich angelegt sein. Schon zu Beginn
des 17. Jahrhunderts entwarf Lord Napier of Merchiston einen Satz
von Holzstäbchen, mit dem man sich Multiplikationstabellen für
mehrstellige Zahlen zusammenstellen konnte. Die Napier-Stäbe wurden
später vielfach variiert und weiterentwickelt, Schickard malte die
Muster auf drehbare Zylinder und setzte sie als Multiplikationsteil
seiner
Rechenmaschine ein. Lord Napier war es
auch,
der die ersten Logarithmentafel publizierte. In
einer Tabelle konnte man nachschlagen, mit welcher Hochzahl man 10
potenzieren muss, um eine bestimmte Zahl zu erhalten. Durch Addition
von Logarithmen konnte man nun Zahlen multiplizieren, durch
Subtraktion dividieren und durch Division Wurzeln ziehen. |
||
|
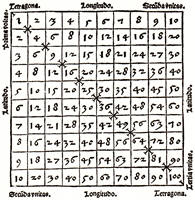
Einmaleinstabelle nach Severinus Boethius um 524 n. Chr. Die Abbildung entstammt seinem Buch "De Arithmetica", das 1488 im Druck erschien (die arabisch-indischen Zahlzeichen sahen zu Boethius' Zeit noch etwas anders aus) |
Die häufigste Hilfstabelle zum Rechen enthält das kleine Einmaleins
und stammt aus der Antike. Bei Leupold findet sich 1727 außer der
quadratischen auch eine dreieckige Variante, die als "tabula
pythagorica "bezeichnet wird. Außerdem gibt es dort eine große runde
Tabelle (siehe unten) und
Additionstabellen für ein- bis zweistellige Zahlen. Allerdings
äußert Leupold die Ansicht, dass die (auswendige) Kenntnis des
kleinen Einmaleins für jeden angehenden Arithmeticus unerlässlich
sei. Weitere Varianten |
|
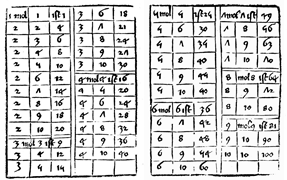
Rechenrezepte im "Bamberger Blockbuch" 1482 Original: Staatsbibliothek Bamberg Nachdruck und Erklärungen: Verlag Saur München 1980 |
Auch nach Gutenbergs Erfindung des Drucks mit beweglichen Lettern erschienen vereinzelt noch "xylographische" Bücher, deren Seiten als Ganzes in eine hölzerne Druckplatte geschnitten waren. Das "Bamberger Blockbuch" ist ein heute nur noch teilweise erhaltenes Heft von 28 Seiten mit Beispielaufgaben, Lösungen und Umrechnungstabellen, die der unbekannte Autor aus Schriften des Regensburger Benediktiners Fridericus Gerhart zusammengestellt hat. |
|
|
Napier-Stäbe John Napier 1550-1617 (Replik 2003 Tropenholz, Herkunft vermutlich Afrika oder Indien) ►Vorführung ►Animation |
Indexleiste als erster Faktor, Vielfachenleisten für 1 bis 9 zur
Zusammenstellung des zweiten Faktors, verwendet als
Multiplikationshilfe.Diagonal nebeneinander stehende Ziffern
benachbarter Leisten sind zu addieren. Zusatzstab zum Ziehen von Quadrat- und Kubikwurzeln. Vorgänger und Nachfolger ►Stephan Weiss ►Peter Kernwein |
|
|
Arithmetische und Geometrische
Progress Logarithmentafel 48 Seiten Jost Bürgi 1620 (Reproduktion 2024) ►Tafel Faksimile ►Tafel mit Erläuterung |
Der Schotte
John Napier hatte 1614 als Erster eine Logarithmentafel
veröffentlicht. 1620 erschien in Prag ein Tabellenbuch des Schweizer
Instrumentenbauers und Astronomen Jost Bürgi. Diese hatte dazu die
Hochzahlen und die Werte von 1,00011 bis
1,0001 23002700 errechnet und
in Zehnerschritten in einer
Tabelle aufgelistet. Im Jahre 1624 veröffentlichte Henry Briggs
erstmals Logarithmen zur Basis 10, die Vereinfachungen beim
Rechnen ermöglichten und bis ins 20. Jahrhundert Verwendung
fanden. ►Rechnen
mit Logarithmen |
|
|
Multiplikationstabelle "eines gewissen Franzosen" nach Harsdörffer 1651 abgebildet bei Jacob Leupolds "Schauplatz der Rechen- und Messkunst" 1727 |
Vielfache (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50 auf Zeiger eingetragen) von 1, 2, 3,..., 10, 20, 30, ..., 100, 200, 300, ... 1000, 2000, 3000, ... 10000 im Kreis angeordnet. Der Zeiger ist drehbar. Nach Harsdörffers Angaben soll die ursprüngliche Scheibe nicht nur aus 14, sondern aus 37 Ringen bestanden haben (so Bischoff 1804). |
|
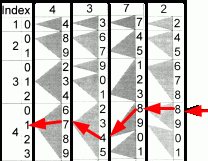
Les Réglettes Multiplicatrices Henri Genaille, Édouard Lucas Frankreich 1885 Nachbau R.A. 2019 ►Animation |
Satz von Holzstäben zur Multiplikation mehrstelliger mit
einstelligen Faktoren. Indexleiste für einstelligen ersten Faktor, Leisten für 0 bis 9 für mehrstelligen zweiten Faktor. Beispiel: 4 x 4372 = 17488 (Im Abschnitt 4 rechts oben (Pfeil) beginnen, dann nach links der Grafik folgen) Weiterentwicklung ►Peter Kernwein ►Stephan Weiss |
|
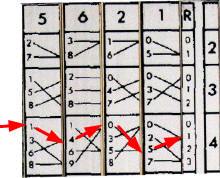
Les Réglettes Multisectrices Henri Genaille Édouard Lucas Frankreich 1885 Nachbau R.A. 2019 |
Satz von Holzstäben zur Division von mehrstelligen durch einstellige
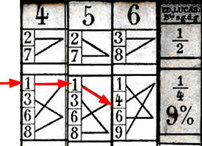
Divisoren. Indexleiste für einstelligen ersten Faktor, Leisten für 0 bis 9 für mehrstelligen zweiten Faktor. Beispiel: 5621 : 4 = 1405 Rest 1 (Indexstab rechts neben Stellenstäbe legen. Einstelligen Faktor auf dem Indexstab suchen. Links in der obersten Zahlenreihe dieses Faktors beginnen und dem Pfeil folgen. In der Spalte R des Indexstabs steht der Rest.) ►Stephan Weiss |
|
Les Réglettes Financières Henri Genaille Édouard Lucas Frankreich 1885 Nachbau R.A. 2019 |
Spezialausgabe der Réglettes Multisectrices für die Zinsrechnung. Die Stäbe sind für die Division durch 2, 4, 6, 8, 9 und 12 eingerichtet. Indem man das Produkt aus Kapital und Tagen erst durch 1000 und dann durch einen dieser Divisoren teilt, erhält man die Tageszinsen für 18%, 9%, 6%, 4,5%, 4% und 3%. 57000 € für 8 Tage kosten bei 9% 114 € Zinsen. Erst im Kopf: 57000 / 1000 * 8 = 456 dann mit Stäben: 456 / 4 = 114 ►Stephan Weiss |
|
|
Theutometer Produkt-Zeiger Merkur Verlag Wehingen, D ca. 1908 (Replik durch Arithmeum)Anleitung |
Laut Packungsaufschrift "ein ägyptischer Rechenstab" (das klingt gehimnisvoll), letztlich aber eine genaue Kopie der Napier-Stäbe in Form von 20 Pappstreifen, vorn und hinten verschieden beschriftet, so dass jede Ziffer viermal zur Verfügung steht. ►Stephan Weiss |

|
Universal Calculator Columbus Calculator Co. (Buchbinderei Franz Kritz) Wien ca. 1920 |
Klapptafel mit einer 3 m langen Doppelskala in 20 Abschnitten. Eine lineare Skala von 0 bis 100 (Ziffern schwarz) ist kombiniert mit einer logarithmischen Skala von 100 bis 1000 (Ziffern rot). Man sucht auf der roten Skala eine Zahl auf und liest daneben auf der schwarzen Skala deren Logarithmus ab. Das wiederholt man mit einer zweiten Zahl. Dann addiert man die Logarithmen, sucht dann auf der schwarzen Skala des Universal Calculators die Summe auf und liest auf der roten Skala das Produkt ab. ►Columbus Addiergerät |
 |
Währungstabelle Nassauische Sparkasse 2001 |
Zugabe bei Umtausch von Deutschen Mark in Französische Franc. |
|
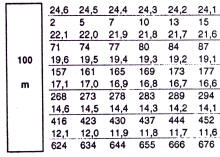
Punktetabelle für die Bundesjugendspiele (100-Lauf, Mädchen) Deutscher Leichtathletikverband 1999 |
Die Formel für die Berechnung der Punktzahl aus der handgestoppten Zeit
lautet P = (100/(Messwert+0,24)-4,0062)/0,00656 Das ist eine nicht nur für Sportlehrer unzumutbare Kopfrechenaufgabe. |
|
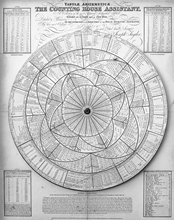
Tabulae Arithmeticae The Counting House Assistant Autor Joseph Taylor Grafik N.L. Hewitt Druck Robert Dutton London, 1814 (Reproduktion eines Originals aus der Sammlung von Valery Monnier) |
Tafel 53 x 66 cm mit 40 Tabellen auf einer drehbaren Scheibe Großes 1x1 Zeit-, Maß- und Währungsumrechnungen |

|
Blitzrechner (D. R. G. M. a) Faltbare Tabelle Nachbau nach Abbildung R.A. 2010 Excel-Tabelle zum Ausdruck |
Additionstabelle von 1+1 bis 24+24, Multiplikationstabelle von 1*1 bis 24*24, gefaltet zum schnellen Nachschlagen. |
|
|
The Lightning Multiplier Copyrighted by The Simplicity Co. Chicago Illinois 1908 |
Einmaleinstafel von 1x1 bis 25x25 in Postkartengröße Umschlag mit Index, Tabelle auf ausziehbarer Karte (Nachbau R.A. 2005) Varianten und Nachfolger |

|
Großes Einmaleins Nestle Vevey, Schweiz 1931 |
Einmaleinstafel von 1x1 bis 20x20 Für alle Schweizer Kantone: Einwohnerzahl, Größe, Eintritt in die Konföderation Umrechnung von Einheiten: Längen, Flächen, Volumina, Hohlmaße, Gewichte |

|
Patenta II Einmaleinsscheibe ca. 1902 |
Vorderseite: 1*2 bis 30x30 Rückseite: 1*31 bis 49*49 |

|
Rechenblitz Bruno Pütz Berlin W36 1950er Jahre |
Zwei Tabellenschieber mit Vorder- und Rückseite 1x1 bis 50x100 auf 4 Tabellen mit jeweils 2 einstellbaren Zeigerpositionen |

|
Rundholzrechenapparat "KUBI" Friedrich Schneider, München angeboten ab etwa 1900, damals als "Cubus" 12 Mark (Der Apparat wird auch heute noch angeboten, das Bild zeigt die aktuelle Ausführung) |
Wenn die Länge eines Baumstamms (in Meter) im roten Feld eingestellt wird und
links oder rechts davon der mittlere Durchmesser (in cm) aufgesucht wird,
kann unter dem Durchmesser das Holzvolumen V=(d/2)²*π*l in Kubikmetern abgelesen werden. Ein ähnliches Gerät entwickelte Friedrich Schneider unter der Bezeichnung "Cubo" für die Berechnung von Kanthölzern. Außerdem bot er Rechengeräte für weitere Anwendungen an. ►Rechnerlexikon |

|
Darnley's Patent Rotable Lightning Calculator,
Pencil Case, Ruler & Measure British Made 1921 |
Einmaleinstabelle 1x1 bis 20x20, darüber drehbarer Zylinder mit Ableselöchern.
Verwendbar zur Aufbewahrung von Stiften, angeblich auch als Lineal oder
zum Messen (6-Zoll-Skala) In Deutschland vertrieben als "Roka, der rechnende Federkasten". |

|
Magic Multiplier Patended Apex Products Corp New York |
Bleistiftaufsatz Folienröhrchen auf Einmaleinstabelle Bereich 2x2 bis 12x12 |

|
Rechenmaschine aus Überraschungsei Ferrero ca. 1986 |
Einmaleinstabellen 2x1 bis 9x5 (Vorderseite) und 2x6 bis 9x10 (Rückseite) auf drehbarem Zylinder unter Plastikquader mit Schaulöchern. |

|
Metric Converter Precisioncraft Kanada 1974 |
Umrechnungsschieber für Längen-, Flächen-, Volumenmaße und Gewichte außerdem Gallonen <-> Liter und Celsius <-> Fahrenheit Luxusausgabe aus Australien |

|
Profilkalkulator Stäbers Wittwe & Co. Eisengroßhandlung Chemnitz 1929 |
Schieber zur Kalkulation von Volumen, Gewicht, Trägheitsmoment, Knickwert und anderen Eigenschaften verschiedener Stahlträgerprofile |

|
Preiskalkulator USA 1. Hälfte des 20. Jahrhunderts |
Zum Einkaufspreis pro Kiste Zitronen (Rückseite: Apfelsinen) gibt die
Scheibe einen empfohlenen Verkaufspreis für das Dutzend an. Verpackte Tabellen |

|
Rechenbuch auf Linien und Ziphren in allerley Handthierung
Geschäften und Kauffmanschafft Adam Ries erstmals 1522 Faksimile der Auflage von 1574 Rechnen wie die Meister Arithmeum/Nicolai |
In mehreren Versionen erschienenes Lehrbuch des Rechnens "auff den
Linihen" (auf einem Rechentisch oder -tuch) und "auff Ziphren" (der schriftlichen
Rechenverfahren). Immer wieder neu zusammengestellt mit
Rechenformeln, Umrechnungsfaktoren, Dreisatzrechnung und Anwendungsaufgaben aus
verschiedenen Lebensbereichen, z.B. einem "Visierbüchlen" zur
Berechnung des Inhalts von Fässern. Auszug |

|
Der bekannte, neue, vermehrte, fehlerfreie
Faulenzer Berechnungen nach Mark und Pfennig Ein Hllfsbuch für jedermann Dr. Chr. Ad. Rise 1844-1958 (Abb.: 1926) insges. 343000 Exemplare |
Sammlung von Tabellen Umrechnung lokaler Maßeinheiten aus Bayern, Baden und Württemberg ins metrische System Umrechnung alter Währungseinheiten in Mark und Pfennig Multiplikationstabellen bis 100x100 berechnung des Volumens von Baumstämmen |

|
Orton's Lightning Calculator Hoy D. Orton Published by W.H. Sadler Baltimore 1875 Preis 1 $ |
Formelsammlung und Rechenanleitung für alle Bereiche des Berufslebens. 216 Seiten mit vielen Abbildungen und Umrechnungstabellen, z. B. Zinstabellen oder eine Tabelle zur Berechnung des Abstands zwischen zwei Kalendertagen. |
|
|
Dekadische Logarithmen (Henry Briggs 1615) Fünfstellige logarithmische und trigonometrische Tafeln Wohlfeile Schulausgabe hrsg. von Dr. Otto Schlömilch Braunschweig (Vieweg), 1897 |
Enthält u. a. - die Brigg'schen Logarithmen der natürlichen Zahlen von 1 bis 10909, - Dimensionen des Erdsphaeroids in geographischen Meilen, von denen 15 auf einen Grad des Äquators gehen, - die Länge der Kreisbögen für Halbmesser Eins, - die Logarithmen der goniometrischen Funktionen der Winkel von Minute zu Minute |
|
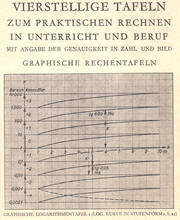
Vierstellige Tafeln zum
praktischen Rechnen in Unterricht und Beruf Philipp Lötzbeyer ab 1918 de Gruyter Berlin |
Zahlentafeln für Quadrate, Quadratwurzeln, Kuben, Kubikwurzel,
Zinsfaktoren, Sterbetafel u.a. Vierstellige Logarithmentafeln der Zehnerlogarithmen von 100 bis 1000 (Differenzangabe für eine weitere Stelle) sowie des Sinus und des Tangens Nomogramm zur grafischen Lösung von quadratischen und kubischen Gleichungen Formelsammlung |

|
Das kleine und große Ein-mal-Eins von 1 bis 100 Heft 14 Seiten A6 J.T.N Deutschland ca. 1910 |
Additions-Tabelle von 1 und 1 bis 9 und 9 Subtraktions-Tabelle von 9 von 9 bis 1 von 1 Multiplikations-Tabelle von 1 mal 1 bis 10 mal 10 Divisions-Tabelle von 1 in 1 bis 9 in 90 Das große 1x1 von 1 mal 11 bis 10 mal 100 Römische Zahlen |
|
|
Weiskircher Doppelblock Schnellrechen-Tafel auch als "Rechenmaschine in Buchform" vermarktet Verlag Wolters & Weiskircher, Hannover 1930 Preis 8,50 RM |
Multiplikationstabellen von1 * 2 bis 999 * 99, aufgeteilt in zwei Blöcke mit Griffregister, außerdem für die Zahlen von 1 bis 1000 die Werte für n², n³, zweite und dritte Wurzel, Logarithmus, Kehrwert, n*p und n²*p/4 |

|
Von der Zahl zum Logarithmus -
vom Logarithmus zur Zahl Wilhelm Friedrich Creutz'sche Verlagsbuchhandlung Magdeburg ab 1931 |
Logarithmentafeln der Zahlen und Winkelfunktionen Anleitung zum Rechenschieber mit Multiplikation, Wurzelziehen, Division, Quadrieren, Sinus- und Tangenswerte etc. |

|
Taschenrechner "Fix" die Rechenmaschine für die Tasche von C. Schade Engelhard-Reyher-Verlag Gotha 1954 7. Auflage Gebrauchsanweisung |
Multiplikationstabellen von 2x100 bis 99x999, außerdem eine Quadrattafel von 1² bis 999². Postkartenformat, 98 Doppelseiten |
|
|
Mathematische Tafeln mit Formelsammlung
E Klett-Verlag, Stuttgart 1981 |
Das Buch enthält Tabellen mit Logarithmen, Winkelfunktionen, Potenzen und Wurzeln, Fakultäten, Binomialkoeffizienten, Zinsfaktoren u.a. |
Rechenwerkzeug.de