Vorwort zur 7. Auflage

Der Taschenrechner „F i x" ist die Rechentafel für jedermann. Schon seit Jahren hat er sich im Berufs-, Geschäfts- und werktätigen Leben, in Büro, Kontor und Werkstatt, besonders auch auf der Reise und bei auswärtiger Tätigkeit als bequemer, praktischer und unentbehrlicher Helfer bewährt.

Der Taschenrechner ermöglicht ein einfaches Ablesen der Produktzahlen, führt in jedem Fall zu einem genauen, einwandfreien Resultat und trägt hierdurch zur Einsparung von Arbeitskraft und Zeit und damit zur Erhöhung der Arbeitsproduktivität bei.

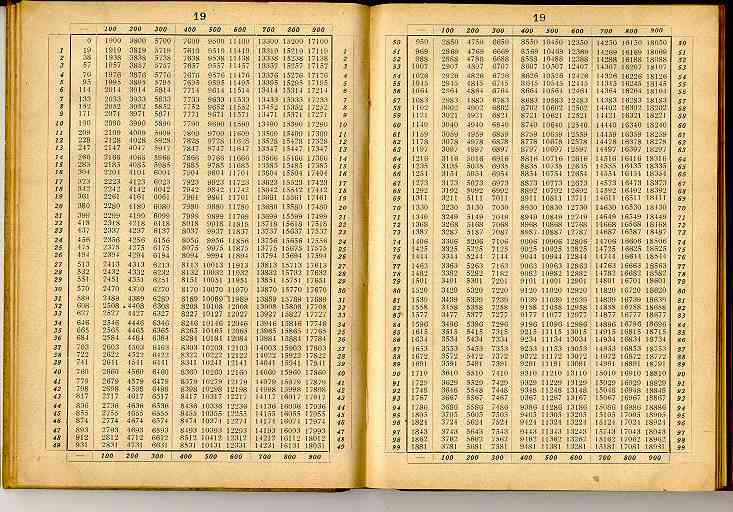
Das Buch umfasst 98 Doppelseiten, welche beginnend mit Seite 2 bis Seite 99 in der oberen Randmitte durchnumeriert sind. Jede Doppelseite ist in 12 senkrechte Spalten geteilt, deren erste (von links) die Randzahlen von l bis 99 enthält, welche in der 12. Spalte wiederholt sind. Die zweite senkrechte Spalte gibt die zu den Randzahlen l bis 99 gehörigen Produkte an, deren zweiten ständigen Faktor die betreffende Seitenzahl darstellt. Die senkrechten Spalten 3 bis 11 enthalten die Produkte der dreistelligen Randzahlen 100 bis 999 mit der Seitenzahl als zweitem ständigem Faktor. Diese dreistelligen Randzahlen, welche in der Tafel nicht direkt ziffernmäßig erscheinen, werden durch Einführung der Kopfzahlen 100 bis 900 (Spalte 3 bis 11) gebildet, dergestalt, dass jede Kreuzungsstelle der senkrechten und waagerechten Zahlenreihen einer dreistelligen Randzahl entspricht, deren Hunderte senkrecht durch die Kopfzahl und deren Zehner und Einer waagerecht durch die Randzahl in der ersten Spalte bezeichnet sind. Man unterscheide also zwischen Seitenzahl, Rand- und Kopfzahl und Produktzahl. Rand- und Kopfzahlen treten durch Fettdruck hervor.

Zur Einführung in den Gebrauch der Tafel sei nachstehende kurze Erklärung an Rechenbeispielen der Beachtung empfohlen. Man gewöhne sich an das Aufschlagen der Seitenzahlen mit der linken Hand, während die rechte notiert.

Am Ende des Buches ist eine Doppeltafel mit den Quadratzahlen von l - 999 beigefügt, deren Benutzung keiner weiteren Erläuterung bedarf.

Der Herausgeber

Dieses Buch wurde gesetzt, gedruckt und gebunden in der Engelhard-Reyherschen Buchdruckerei, Gotha, Siebleber Straße 24.
Copyright 1954 by Engelhard-Reyher-Verlag, Gotha V/6/17-10 130/8G/51

 

Das Multiplizieren

l. Beispiel:

36 x 57 (Faktoren) = 2052 (Produkt)

Man schlage die Seitenzahl 36 (Doppelseite) auf und suche in der ersten senkrechten Spalte (links) die Randzahl 57; waagerecht neben letzterer in der zweiten senkrechten Spalte findet man die gesuchte Produktzahl 2052,

Selbstverständlich kann man auch Seite 57 aufschlagen und liier die Randzahl 36 aufsuchen; man findet dann in der zweiten Spalte dieselbe Produktzahl (2052).

Beachte: Bei zwei ein- oder zweistelligen Faktoren steht die Produktzahl s t e t s in der zweiten senkrechten Spalte!

II. Beispiel :

57 x 389 = 22173

Man suche auf Seite 57 die Randzahl 89 und die Kopfzahl 300 (389 = 300 + 89); wo sich die von dieser ausgehende senkrechte Zahlenreihe mit der durch die Randzahl gegebenen waagerechten Zahlenreihe kreuzt, findet man die Produktzahl (22173).

Beachte: Soll eine zweistellige Zahl mit einer drei- (oder mehr-)stelligen Zahl multipliziert werden, so ist stets die durch die zweistellige Zahl gegebene Seite aufzuschlagen!

III. Beispiel:

57 x 8536   = 57 x   36     2052

            + 57 x 8500   484500

                          486552

Man suche auf Seite 57 die Randzahlen 36 und 85 auf und schreibe die in der zweiten Spalte zu ihnen gehörigen Produktzahlen untereinander, nachdem man an die zweite Produktzahl zwei Nullen angehängt hat, so dass diese um zwei Stellen nach links rückt; ihre Summe ergibt das Gesamtprodukt 486552.

Will man den zweiten Faktor dreistellig zerlegen, so ergibt sich:

  57 x  536 =  30552

+ 57 x 8000 = 456000

              486552 

 

IV. Beispiel :

57X468536   = 57 x    536      30552

            + 57 x 468000   26676000

                            26706552

Auf Seite 57 findet man zur Randzahl 36 unter Kopfzahl 500 die Produktzahl 30552 und zur Randzahl 68 unter Kopfzahl 400 die Produktzahl 26676. Letzterer hänge man 3 Nullen an und addiere sie zu ersterer, so ergibt sich das gesuchte Gesamtprodukt 26706552.

V. Beispiel:

957x536     = 957 X 86   34452

            + 957 x 500 478500

                        512952

Es ist hier einerlei, ob man den ersten oder zweiten Faktor zerlegt; lautete aber der erste Faktor statt 957 etwa 157 oder 951, so würde man einen Seitenaufschlag ersparen, wenn man diesen zerlegte.

VI. Beispiel:

957 X 8536 = 957 x   36    34452 (s. Seite 36)

            + 957 x 8500  8134500 (s. Seite 85)

                          8168952

Bei größerer Stellenzahl der Faktoren empfiehlt es sich, den kleineren Faktor zweistellig, den größeren Faktor dreistellig von rechts nach links abzuteilen und zur Nachprüfung des Produkts die Neunerprobe anzuwenden.

VII. Beispiel:

457382 x 6493  =   93 x    382       35526

               +   93 x 457000    42501000

               + 6400 x    382     2444800

               + 6400 x 457000  2924800000

                                2969781326

Man ermittele die Quersummen beider Faktoren und des Produkts durch Addition ihrer einzelnen Ziffern, subtrahiere von jeder dieser Quersummen die Zahl 9 oder ein Vielfaches derselben und multipliziere die aus den Quersummen der beiden Faktoren hiernach verbleibenden Reste miteinander: so muss das Ergebnis mit der aus der Quersumme des Produkts verbleibenden Restzahl übereinstimmen, bzw. um ein Vielfaches von 9 größer sein. Andernfalls liegt ein Rechenfehler vor. Im vorstehenden Beispiel

                     457382 x  6493  = 2969781326

die Quersummen sind      29      22            53

das Vielfache von 9     —27     —18          — 45

Rest                      2     x 4           = 8

Sind die Faktoren eines Produkts Dezimalzahlen, so trennt man bei der Produktzahl die Summe ihrer Dezimalstellen durch das Komma von rechts nach links ab, z. B.:

               457,382 X 64,93 = 29697,81326

Zinssätze zu Bruchteilen wird man zweckmäßig in Dezimalzahlen verwandeln und mit letzteren multiplizieren, z. B.:

statt mit l 5/4 mit 1,80

statt mit 2 3/4 mit 2,75

statt mit 3 2/3 mit 3,667

statt mit 4 3/5 mit 4,60

statt mit 5 1/2 mit 5,50

statt mit 6 2/5 mit 6,40

statt mit 7 1/3 mit 7,333

statt mit 8 1/4 mit 8,25

statt mit 9 1/5 mit 9,20

Die Produkte zweier gleich lautenden Faktoren (Quadrate) von l bis 999 sind am Schlüsse auf einer Sondertafel zusammengestellt.

Das Dividieren

V11I. Beispiel:

486552 (Zähler)

--------------- = 8536 (Quotient)

  57 (Nenner)

Man schlage den Nenner Seitenzahl 57 auf, suche diejenige vierstellige Produktzahl, welche, von links nach rechts gerechnet, dem Zähler gleich oder die nächst kleinere ist, und findet 4845 mit der zugehörigen Randzahl 85 als ersten Teilquotienten. Man subtrahiere die gefundene Produktzahl von den ersten vier Stellen des Zählers, füge dem Rest die weiteren Stellen des Zählers an, suche in derselben Weise den zweiten Teilquotienten und schreibe ihn hinter den ersten. Man erhält den gesuchten Quotienten mit 8536, und die Division geht hier restlos auf.

57 / 486552 = 85 36

     4845

      2052

      2052

    Rest O

IX. Beispiel;

7963482

--------= 139 710 Rest 12

57

 

57 / 79634827923 = 139710 12

     7923

       40482

       40470

          12

 

X. Beispiel:

81691558

-------- = 85362 Rest 124

   957

Man runde den Nenner von links nach rechts auf zwei Stellen, also auf 96, ab, suche auf dieser Seite diejenige Produktzahl, welche den ersten vier Ziffern des Zählers gleich oder die nächst kleinere ist, also 8160; die zu ihr gehörige Randzahl 85, welche die ersten Ziffern des Quotienten darstellt, schlage man als Seitenzahl auf und findet hierunter Kopfzahl 900 zur Randzahl 57 die Produktzahl 81345, welche, von den ersten fünf Stellen des Zählers abgezogen, den Rest 346 ergibt. (Hätte man den Nenner auf 95 abgerundet, so hätte man auf Seite 95 als nächst niedrigere Produktzahl 8075 und als Randzahl gleichfalls 85 gefunden.) Nachdem man dem Rest 346 zwei weitere Ziffern des Zählers angefügt hat, sucht man in derselben Weise den zweiten Teilquotienten und verfährt weiter, wie die folgende Ausrechnung zeigt:

957 / 81691558 = 85 36 2

      81345

        34655

        34452

          2038

          1914

      Rest 124

 

 

957 |124 = 0,1295...

     1240

      957 '

      2830

      1914

       9160

       8613

        5470 usw

 

85362

    0,1295...

85362,1295...

Will man den Rest 124 durch Dezimalzahlen ausdrücken, so führt man die Division in der oben rechts angegebenen Weise bis zu dem gewünschten Genauigkeitsgrad weiter und hängt dem durch ein Komma abgetrennten Quotienten die gefundenen Dezimalen an.

Handelt es sich beim Zähler oder Nenner oder bei beiden um Dezimalzahlen, so verwandelt man diese zunächst in bruchfreie Zahlen, indem man Zähler und Nenner sooft mit 10 multipliziert, als die größere Zahl der Dezimalstellen eines der beiden beträgt. Ist die Zahl der Dezimalstellen beim Zähler größer als beim Nenner, so trennt man nach Ausführung der Division wieder soviel Stellen (von rechts nach links) durch Komma ab, als man an den Nenner Nullen angehängt hat, z.B.:

486,552    486552

------- = -------- = 85,36

  5,7      5700

Auch beim Dividieren kann man sich durch sinngemäße Anwendung der Neunerprobe davon überzeugen, ob das errechnete Resultat richtig ist.

An Hand der Beispiele wird jedermann in kurzer Zeit sich in den Gebrauch der Tafel eingewöhnen und vor allem bei längerer Übung die Ersparnis an Zeit und Kopfarbeit wie den Vorteil eines gesicherten Rechnens schätzen lernen.

Rechenwerkzeug.de