Drehen oder Schieben: Wie rechnet sich's leichter?
Dr. Philipp Lötzberger, geboren 1881 in Sobernheim, promoviert 1903 in
Straßburg, später wohnhaft in Berlin, im Hauptberuf vermutlich Gymnasiallehrer, war der
Autor einiger erfolgreicher Tafelwerke, Lehrbücher und Aufgabensammlungen, etwa
"Geometrie
und geometrisches Zeichnen",
"Vierstellige Tafeln zum Logarithmische
Dieser Philipp Lötzberger erhielt am 18. Oktober 1923 das Patent DRP 383821 auf ein neuartiges Rechengerät. Er bezeichnete es als "Nomographische Rechen- und Ablesemaschine" oder kurz als "Rechendreher", weil bei diesem Gerät nicht zwei Skalen gegeneinander verschoben, sondern ein Nomogramm mittels eines Drehknopfs über zwei Walzen unter einem Ablesefenster gedreht wurde.
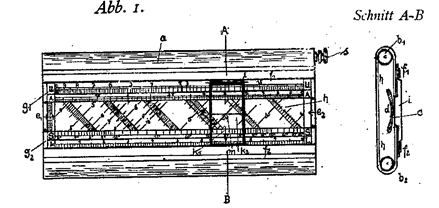
Den Zweck dieses Geräts beschreibt er wie folgt:
"Die nomographische Rechen- oder Ablesemaschine soll dazu dienen, die im praktischen Leben, insbesondere der Technik vorkommenden Rechnungen, welche in den meisten Fällen nur einen beschränkten Genauigkeitsgrad erfordern, schnell und sicher auszuführen oder bei verwickelten Größenbeziehungen, deren Inhalt durch geeignete Zeichnungen (Nomogramme besonderer Art) niedergelegt werden kann, alle für den betreffenden praktischen Zweck in Betracht kommenden Zahlenlösungen mit hinreichender Genauigkeit bequem ablesen zu können."
Die Skalen
![]()
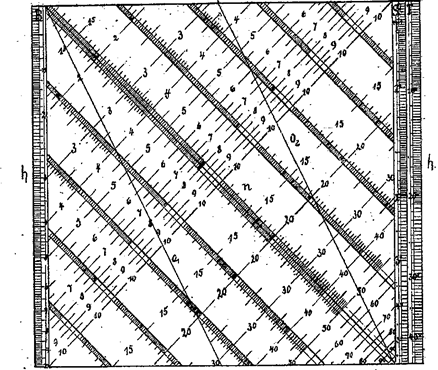

Das Quadrat mit den parallel angeordneten diagonal verlaufenden Skalen läuft als breites Band um zwei Walzen. Sichtbar ist immer nur ein Ausschnitt. Auf dem Band befinden sich links und rechts neben dem Quadrat eine logarithmische Skala B von 1 bis 10 und links das Skalenpaar S und T (Gradzahlen von 0 bis 5° bzw. 5° bis 45° zur Ermittlung des Sinus bzw. Tangens.
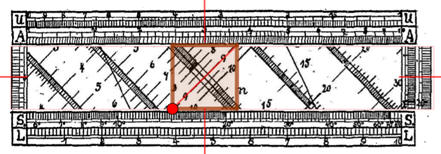
Die beiden horizontalen Skalenpaare U/A und S/L befinden sich oberhalb
und unterhalb des sichtbaren Ausschnitts der Bandskalen auf dem Gehäuse.
Über dem Ausschnitt ist ein verschiebbarer Läufer mit einer horizontalen, einer vertikalen und einer diagonalen Indexlinie angebracht. So werden anders als beim Rechenschieber beide Operanden und das Ergebnis einer Rechnung gleichzeitig in den Blick genommen und durch den Läufer einander zugeordnet.
Ob der "Rechendreher" in der patentierten Form je über das Prototypstadium hinausgekommen ist, ist unklar. Um die Wende vom 9. zum 20. Jahrhundert hatten Unmengen von unterschiedlichen Kleinrechengeräten, vorwiegend Addierer, jeweils ihren eigenen Markt gefunden. Zwischen den beiden Weltkriegen war die klassische Form des Rechenschiebers in deutschen Schulen jedoch schon so verbreitet, dass alternative Konzepte zumal mit aufwendigerer Hardware wenig Chancen hatten, sich im Markt durchzusetzen. Ein ähnlches Schicksal ereilte in den 1950er Jahren den exotischen Tyler-Rechner und in den 1960er Jahren den eigentlich pädagogisch ziemlich genialen Entwurf der Brüder Wern (ABC-Rechner IWA 1638). In allen diesen Fällen galt nicht "Das Bessere ist des Guten Feind", sondern "Gegen das Gewohnte kämpfen auch Genies vergebens."
Der Erfinder behauptet: "Der Rechendreher stellt eine Rechenvorrichtung dar, die gegenüber dem weit verbreiteten Rechenschieber bedeutende Vorzüge aufweist. Insbesondere ist er für den mechanischen Gebrauch leichter verständlich als der Rechenschieber."
Mit meiner Animation (leider nur in 2D, deshalb wird hier doch wieder nur geschoben und nicht gedreht) können Sie diese Aussage verifizieren, indem Sie die folgenden Anwendungen ausprobieren.
Anwendungen (Auszug aus der Patentschrift)
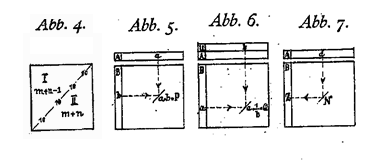
"1. Multiplikation (Abb. 5). Da die Tafel eine
Multiplikationstafel darstellt, ist zu beachten, daß auf den Skalen A und B die
Faktoren stehen und das Produkt auf der Rolltafel abzulesen ist. Zur
Bestimmung des Produktes a • b = P zweier Zahlen stellt man daher den Läufer mit
dem senkrechten Strich auf a der Skala A, dreht die Rolltafel, bis der Zeiger
des Ausschnittes über b der Skala B steht, und liest dann das Ergebnis am
Schrägstrich des Läufers auf der Rolltafel ab. Beispiel: 5,2*3 = 15,6.
Die Verwendung des Rechendrehers als Produktentafel erfordert nur eine Drehung.
2. Division (Abb. 6) a/b = 4,8 / 1,6 = 3 Erst wird der Divisor b = 1,6 auf B (oder Ä) und dann der Läufer mit dem Schrägstrich über a = 4,8 der Rolltafel eingestellt. Das Ergebnis Q = 3 (der andere Faktor) ist auf der Skala A (oder B) abzulesen. Die Skala U ermöglicht, die Division entsprechend wie die Multiplikation durchzuführen.
Bestimmung der Stellenzahl: Die
Rolltafel wird durch den Zehnerstrich (Abb. 4) in zwei kongruente Rechenfelder I
und II eingeteilt. Sind m und n die Stellenzahlen der Zahlen M und X, so ist, je
nachdem ob das Ergebnis im Feld I oder II erscheint, die Stellenzahl
des
Produktes P=M*N p=(m+n-1) (I) oder p=m+n (II) und des Quotienten Q=M/N
q=m-n+1 (I) oder q=m-n (II).
3. Vereinigte Multiplikation und Division. Alle
Dreisatzaufgaben (Aufgaben von der Form x = a/b*c) können durch eine Drehung
ohne Ablesung eines Zwischenergebnisses gelöst werden.
Zinsaufgaben sind bequem
mit Hilfe der Zinszahlenformel Z = (1/100*k*t)/d = N/d zu lösen (Abb.
7).
4. Zweite Potenzen und Wurzeln werden mit Hilfe der Diagonalskala ermittelt.
5. Dritte Potenzen und Wurzeln werden mit Hilfe der 3. Potenzlinien o1 und o2 bestimmt, höhere Potenzen mit Hilfe besonderer Potenzlinien oder der Skala L.
6. Ermittlung von Funktionswerten, z. B. von a/bx, ax³ usf. und der Lösungen von Gleichungen.
7. Bestimmung der Werte trigonometrischer Funktionen und Ausführung trigonometrischer Rechnungen, z. B. mit dem Sinussatz.
8. Berechnung der Inhalte von Flächen und Körpern. Gewichtsbestimmungen. Die Skala U ermöglicht das Produkt a*b*c mit Hilfe einer Drehung zu bestimmen.
Rechenmarken können genau wie beim Rechenstab angebracht werden. Je nach dem besonderen Rechenzweck kann der Rechendreher zur Erzielung der bequemsten Lösung umgestaltet werden. Weitere Skalen oder besondere Linien können ohne Belastung der Vorrichtung angebracht werden."
Vorschlag für Bastler und Tüftler: Ein alternativer Schieber
Lötzbergers Patentansprüche beziehen sich in erster Linie auf den mechanischen Aufbau. Der ist aber in handlicher Form nur bei sehr begrenzter Genauigkeit zu realisieren. Wenn man das in Kauf nimmt, kann man wiederum die Skalenanordnung aus dem Patent auch gleich mit sehr viel geringerem Aufwand auch gleich statt als "Schieber" auf Pappe statt als "Dreher" realisieren.
Falls Sie also gerade Lust auf ein Bastelstündchen haben, empfehle ich Ihnen, die letzte Seite des Patents mit den Skalen auf Postkartenkarton auszudrucken, mit einem Cuttermesser ein Fenster in einen farbigen Karton zu schneiden, den Sie als Hülle um das zweidimensionale Skalensystem herumwickeln. Dann fehlt noch ein Läufer, den man aus einer alten Overheadfolie herstellen kann und fertig ist der "Verbesserte zweidimensionale Rechenschieber":

Wenn Sie einen 3D-Drucker Ihr Eigen nenen, können Sie natürlich auch versuchen, den "Rechendreher" nach den Angaben im Patent nachzubauen, am besten mit exakt berechneten Skalen. Wenn Sie das schaffen, veröffentliche ich hier gern ein Foto.
Rechenwerkzeug.de