Vergleichstest 1906
|
Gut zehn Jahre mag es her sein, dass ein neuer kompakter Rechenmaschinentyp die Bureaus eroberte: das "Odhner Arithmometer", eine Konstruktion des Schweden Willgod T. Odhner aus Sankt Petersburg, die in Deutschland besser bekannt ist unter dem Namen "Brunsviga", weil sie in Braunschweig erfolgreich in Lizenz produziert und eigenständig weiterentwickelt wird. Zwar ist eine solche Sprossenradmaschine deutlich kleiner, kompakter und preiswerter als die seit Jahrzehnten eingeführten Staffelwalzenmaschinen vom Typ des "Thomas Arithmomètre", doch kostet sie immer noch vierhundert Mark, ein Betrag, der von einem kleinen Kaufmann unmöglich investiert werden kann. Im letzten Herbst nun erschien auf dem Markt die "Omega Rechenmaschine" aus der Münchener "Präzisions-Maschinenfabrik" von Justin Wilhelm Bamberger, der zuvor eine ähnliche Konstruktion aus Amerika importiert hatte. Zunächst für lediglich 35 Mark angeboten - was für einen Arbeiter immerhin einen halben Monatslohn bedeutet -, erwies sich das erste Modell offenbar doch als etwas zu leicht gebaut und dem harten Büroalltag nicht gewachsen. So wurde nun bereits nach wenigen Monaten ein verbessertes "Modell 3" zum Preis von nunmehr 48 Mark aufgelegt.
Der Hersteller wirbt mit den Prädikaten "schnell,
einfach, praktisch, dauerhaft" und "BILLIG".
Nichtsdestoweniger behauptet er: "Selbst die größten
Multiplikationen und Divisionen werden auf der 'Omega' mit einer
Schnelligkeit ausgeführt, die auch von vielen sehr teueren Maschinen
nicht übertroffen wird. Man wird erstaunt sein, wie leicht diese
Operationen auszuführen sind."  Anzeige aus dem "Simplicissimus" von Oktober 1905 |
|
|
Vergleichen wir also... |
|
 Original Odhner Modell A |
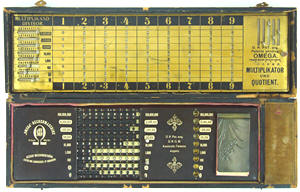 Bamberger Omega |
| Funktionsprinzip: Die Maschine arbeitet mit Sprossenrädern, das sind Zahnräder mit einstellbarer Zähnezahl, die die Werte des Einstellregisters ins Resultatregister übertragen, ohne dabei mit dem Übertrag von einer Stelle zur nächsthöheren in Konflikt zu kommen. Die Maschine besteht aus knapp 1000 Einzelteilen, davon viele hochpräzise Zahnräder, Achsen und Federn aus Messing oder Eisen. |
Funktionsprinzip: Die Maschine ist ein "Zahlenschieber", aber sie arbeitet noch horizontal nach dem Prinzip des Abakus, nur dass nicht Ringe hin- und hergeschoben werden, sondern Marken auf einem Stab. Im Deckel befinden sich weitere, teilweise verdeckte Zahlenschieber, die nach dem Prinzip der Napier-Stäbe die letzte Stelle eines Produkts mit dem Übertrag aus der vorigen Stelle kombinieren. Die Maschine besteht aus etwa 250 Einzelteilen aus Holz, Blech, Samt Stahlfedern, Nägeln und Blechkappen. |
| Löschen: ♦ Schieber im Einstellwerk auf Null stellen. ♦ Umdrehungszählwerk und Resultatwerk mit jeweils einer Drehung der zugehörigen Flügelmutter löschen. ♦ Taste drücken und Wagen nach links fahren. Dauer: 8 s |
Löschen: ♦ Alle Schieber im Additionsteil nach rechts schieben. ♦ Alle Schieber im Mutltplikanden nach rechts und im Multiplikator nach unten schieben. Dauer: 5 s |
 Addition 374+451: ♦ 374 über die Schieber im Einstellwerk eingeben ♦ Kurbel einmal im Uhrzeigersinn drehen ♦ 451 über die Schieber im Einstellwerk eingeben ♦ Kurbel einmal im Uhrzeigersinn drehen ♦ Ergebnis 825 im Resultatwerk ablesen Dauer: 12 s |

Addition 374+451: ♦ 374 von der Einerstelle nach oben einstellen. Dabei Schieber von der Ziffer nach links bis Anschlag ziehen. ♦ 451 von der Einerstelle nach oben addieren: Falls die jeweilige Ziffer schwarz unterlegt ist (hier bei 1), Schieber nach links ziehen. Falls die jeweilige Ziffer hell unterlegt ist (hier bei 5), Schieber nach rechts ziehen und den nächsthöheren Schieber mit der anderen Hand um 1 nach links. Dabei können auch Überträge über mehrere Stellen auftreten (99+1). ♦ Ergebnis 825 von oben nach unten in den runden Fenstern Dauer: 12 s |
| Subtraktion 1045-737: ♦ 1045 über die Schieber im Einstellwerk eingeben ♦ Kurbel einmal im Uhrzeigersinn drehen ♦ 737 über die Schieber im Einstellwerk eingeben ♦ Kurbel einmal im Gegenuhrzeigersinn drehen ♦ Ergebnis 309 im Resultatwerk ablesen Dauer: 15 s |
Subtraktion 1045-737: ♦ 1045 von der Einerstelle nach oben einstellen. Dabei Schieber von der Ziffer nach links bis Anschlag ziehen ♦ 737 von der Einerstelle nach oben subtrahieren: Falls die jeweilige Ziffer, diesmal die rote Komplementärzahl, hell unterlegt ist, Schieber nach rechts ziehen. Falls diese Ziffer dunkel unterlegt ist, Schieber nach rechts ziehen und den nächsthöheren Schieber mit der anderen Hand um 1 nach links. Dabei können Überträge über mehrere Stellen auftreten (100-1). ♦ Ergebnis 309 in den Fenstern ablesen Dauer: 20 s |
 Einstelliges Vielfaches 478*7: ♦ 478 über Schieber im Einstellwerk eingeben ♦ Kurbel sieben Mal drehen ♦ Ergebnis 3346 im Resultatwerk ablesen Dauer: 10 s |
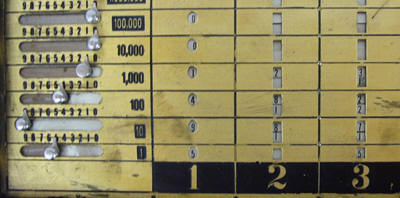 Einstelliges Vielfaches 478*7: ♦ 478 im Deckel über Schieber links eingeben ♦ Vielfaches in den kleinen Fenstern über der 7 ablesen. Dabei müssen Ziffern, die übereinander im gleichen Fenster stehen im Kopf addiert werden. Häufig treten Überträge zwischen den Stellen auf: 478*7 = 2 8+4 9+5 6 = 3346 ♦ Ergebnis 3346 in den Fenstern ablesen Dauer: 12 s |
 Multiplikation 1493*216: ♦ 1493 über Schieber im Einstellwerk eingeben ♦ Kurbel sechs Mal im Uhrzeigersinn drehen ♦ Wagen um eine Position nach rechts verschieben ♦ Kurbel einmal im Uhrzeigersinn drehen ♦ Wagen um eine Position nach rechts verschieben ♦ Kurbel zwei Mal im Uhrzeigersinn drehen ♦ Ergebnis 322488 im Resultatwerk ablesen Dauer: 18 s |
 Multiplikation 1493*216: ♦ 1493 im Deckel links einstellen ♦ 216 im Deckel rechts merken ♦ Sechsfaches ablesen, Ziffern addieren und mit Einerstelle beginnend ins Addierwerk übertragen ♦ Einfaches ablesen, Ziffern addieren und mit Zehnerstelle beginnend ins Addierwerk übertragen. Dabei Regeln unter "Addition" beachten. ♦ Zweifaches ablesen, Ziffern addieren und mit Zehnerstelle beginnend ins Addierwerk übertragen. ♦ Ergebnis 322488 in den Fenstern ablesen Dauer: 56 s |
| Division 8357:14: ♦ Wagen ganz nach links ♦ 8357 beginnend ab Stelle 6 nach rechts einstellen ♦ Kurbel einmal im Uhrzeigersinn drehen ♦ Umdrehungszählwerk löschen ♦ 14 beginnend mit Stelle 6 nach rechts einstellen ♦ Kurbel so oft im Gegenuhrzeigersinn drehen, bis Glocke ertönt, dann noch einmal im Uhrzeigersinn drehen. ♦ Wagen um eine Position nach rechts verschieben ♦ Kurbel so oft im Gegenuhrzeigersinn drehen, bis Glocke ertönt, dann noch einmal im Uhrzeigersinn drehen. ♦ Wagen um eine Position nach rechts verschieben ♦ Das Verfahren kann fortgesetzt werden, solange im Resultatwerk Stellen zur Verfügung stehen. ♦ Wenn Wagen den Anschlag errecht hat, Ergebnis 596,92.. ablesen und Kommaposition überschlagen Dauer: 58 s |
Division 8357:14: ♦ 8357 im Addititonsteil einstellen ♦ 14 im Deckel links einstellen ♦ Feststellen, welches das höchste Vielfache von 14 ist, das in die 83 passt. Es ist 70, also das 5-fache. ♦ 70 von oben beginnend nach den Regeln der Subtraktion abziehen. Der Rest ist 1357. ♦ Ziffer 5 im Quotientenschieber merken ♦ Feststellen, welches höchste Vielfache von 14 in die höchsten Stellen von 1357 passt. Es ist 126, das 9-fache. ♦ 126 von oben beginnend nach den Regeln der Subtraktion abziehen. Der Rest ist 97 ♦ Ziffer 9 im Quotientenschieber merken ♦ Feststellen, welches höchste Vielfache von 14 in 97 passt. Es ist 84, das 6-fache. ♦ 84 von oben beginnend nach den Regeln der Subtraktion abziehen. Der Rest ist 13 ♦ Ziffer 6 im Quotientenschieber merken ♦ Im Qoutientenschieber steht jetzt das Ergebnis 596. Falls zwei Kommastellen ermittelt werden sollen, wird die 8357 um einige Stellen nach oben verschoben und später im Erbgebnis zwei Stellen durch Komma abgetrennt. Vorsicht ist geboten bei sehr kleinen Resten. Nach der ersten Subtraktion darf der Divisor immer nur um eine Stelle nach unten wandern. Ist der darüber liegende Rest kleiner als der Divisor, muss eine 0 im Quotienten eingefügt werden. Dauer: 115 s |
 |
 |
| Fazit: Die Odhner ist eine echte "Maschine", d.h. die mathematischen Gesetzmäßigkeiten sind in mechanische Abläufe übersetzt. Überträge werden automatisch berücksichtigt. Es gibt Sicherheitsvorkehrungen: Bei ungenauer Einstellung im Einstellwerk blockiert die Kurbel, bei nur teilweiser Kurbeldrehung das Einstellwerk. |
Fazit: Die Omega ist keine Maschine im engeren Sinn, sie stellt lediglich beschriftete Schieber als Zahlenrepräsentanten und Merkhilfen, zur Verfügung. Dabei muss der Benutzer zunächst einmal umlernen: Die Ziffern stehen nicht neben- sondern übereinander. Wegen der Überträge ist es sinnvoll, Zahlen beginnend mit der kleinsten Stelle abzulesen und einzugeben, dies aber erfordert weiteres Umdenken. |
| Wie man leicht feststellt, besteht die menschliche Tätigkeit hier überwiegend aus Einstellen, Kurbeln, Zählen, Auf-das Ertönen-der-Glocke-Warten und Ablesen. | Die
Regeln der Zahlenverarbeitung müssen vom Benutzer gelernt und
befolgt werden. Für jede der vier Grundrechenarten sind jeweils drei
bis vier Regeln zu verinnerlichen. Bei Multiplikation und Division
bei der Übertragung von der Vielfachentafel ins
Addierwerk bis zu drei einstellige Zahlen im Kopf addiert werden. |
| Das
Rechnen mit der Odhner erfordert zwar etwas Körperkraft, aber keine
übermäßige Konzentration. Viele Fehler (z.B. eine überzählige
Kurbeldrehung oder ein falsch eingegebenener Summand in einer
Zahlenreihe) sind nachträglich gut korrigierbar. Zwar laufen die Zahnräder mitunter etwas rau, insgesamt hat man aber das Gefühl, dass Einstellhebel und Anzeigeräder präzise einrasten. |
Das Rechnen mit der Omega erfordert höchste
Konzentration. Die Abläufe gehen, insbesodere wenn verschiedene
Rechenarten vermischt vorkommen, auch nach längerem Training nur
teilweise in Fleisch und Blut über. Passiert ein Fehler, so muss
man in der Regel von vorn beginnen. Da insbesondere bei
Multiplizieren und Dividieren die Fehlerquellen steigen, wächst die
benötigte Zeit überproportional zur Kompexität der Aufgabe. |
| Die benötigte Zeit liegt insbesondere bei komplizierteren Aufgaben deutlich unter der für Kopfrechnen oder schriftliches Rechen. | Die benötigte Zeit liegt bei Addition und
Subtraktion etwas unter der für schriftliches Rechnen. Bei
Multiplikation und Division ist insbesondere wegen der
Fehleranfälligkeit der Umdenkprozesse kein wirklicher Zeitvorteil erkennbar. |
| Einzelne Punkte sind
noch verbesserungsfähig: ♦ Das Einstellwerk sollte mit einem Hebel komplett gelöscht werden können. ♦ Ein Mechanismus sollte verhindern, dann man den Wagen versehentlich um zwei statt um eine Stelle verrückt. ♦ Gelegentlich "überschleudern" bei zu schnellem Drehen die Zahnräder, d.h. sie drehen ein Stück über die Raste hinaus. ♦ Die Qualität ist nach dem Stand der Technik optimal, konstruktive Fortschritte scheinen noch möglich. |
Das Gerät ist nur bedingt verbesserungsfähig: ♦ Trotz der Herstellung in einer "Präzisionsmaschinenfabrik" sind die Bestandteile der Omega mit relativ großen Toleranzen gefertigt. Die Multiplikationsschieber rasten nicht ein. Die Ziffern sind sehr klein und stehen häufig nicht in der Mitte des Fensters. Der Anschlag der Schieber ist nicht genau definiert. ♦ Auch scheinen die Materialien nicht auf harte Beanspruchung und große Dauerhauftigkeit ausgelegt. ♦ Die vielen erforderlichen Denkprozesse und die geringe Fehlertoleranz sind Systemmängel und nicht zu beheben. |
|
Anmerkung (2017): Im Prospekt zum "Universal-Rechenapparat" werden von Bamberger erheblich kürzere Rechenzeiten angegeben, die von geübten Benutzern noch unterboten werden sollen - und das alles noch auf einem Zahlenschieber ohne Multiplikationshilfe. Tatsächlich gab es in Russland und China noch vor wenigen Jahren Rechner, die auf einem Abakus atemberaubendes Tempo vorlegten. Allerdings hatten die das bereits in der Schule gelernt und jahrelang geübt. Für Leute, die sich im Erwachsenenalter mal schnell eine "Rechenmaschine" anschaffen, waren solche Zeiten wohl völlig illusorisch, zumal aus Gründen der Baumaße und Präzision an ein blindes Bedienen nicht zu denken ist. Nachfolger der Odhner gab es bis etwa 1970. Die Omega wurde dagegen wohl nur von Ende 1905 bis Anfang 1907 produziert. Die beantragten Patente wurden nie erteilt, der Gebrauchsmusterschutz war bereits dem Vorgängermodell "Universal" zugesprochen worden. Justin Wilhelm Bamberger, ein rühriger, junger Kaufmann und findiger Techniker, befasste sich ab 1907 vor allem mit der Produktion billiger Schreibmaschinen, für die er auch mehrere Patente erhielt. Um 1912 wechselte er nach zahlreichen Umfirmierungen die Branche und hinterließ danach keine Spuren mehr im kollektiven Gedächtnis (siehe ►Rechnerlexikon). Justin Bamberger verfügte wohl schon früh über gute Verbindungen in die USA und kannte den dortigen Markt. Hätte er nach Frankreich geschaut, wäre ihm vielleicht der Rechner von Michel Rous (1869) aufgefallen, der ebenso wie die Omega einen abakusähnlichen Addierer mit einem Napier-Multiplizierer kombiniert.  Rechner von Michel Rous, Collection IBM-Europe. Foto Photo J.-M. Ramès © Inria.fr INRIA-0117-011.jpg Beim Blick nach Frankreich wäre ihm aber sicher erst recht das Urmodell aller Zahlenschieber aufgefallen. Dieser war bereits 1849 von Kummer in Russland patentiert worden und wurde in Frankreich seit 1887 von Troncet erfolgreich als "Arithmographe" vermarktet. Auch Troncet ließ sich übrigens um 1907 ein Modell mit Multiplikationstafel patentieren. Die Zahlenschieber dieses Typs mussten zwar mit Stift bedient werden, aber sie waren sehr viel kleiner als Bambergers Maschinen, sie ordneten die Ziffern einer Zahl in der gewohnten Weise horizontal an und sie verfügten über eine zwangsweise Kontrolle des richtigen Übertrags. Ihre Erfolgsgeschichte begann in Deutschland kurz nach 1910, und sie dauerte bis 1970. |
|
| .. aber ein schönes Spielzeug ist die Omega doch! | |
Rechenwerkzeug.de