Logaritmal-Rechentafel
(Originalgröße 11x17 cm)
Bei der Logaritmal-Rechentafel wurde die Rechenstabskala in mehrere parallele Abschnitte zerlegt. Trotz der Gesamt-Skalenlänge von 1,5 m ist das Gerät nur postkartengroß. Allerdings hat er einen Nachteil: Während bei den Rechenwalzen und beim Multiplex die eine Skala doppelt aufgetragen ist, damit kein Ergebnis außerhalb der Skala liegt, muss man beim Logaritmal bei jeder Multiplikationsaufgabe zwischen vier möglichen Auflegepositionen entscheiden.
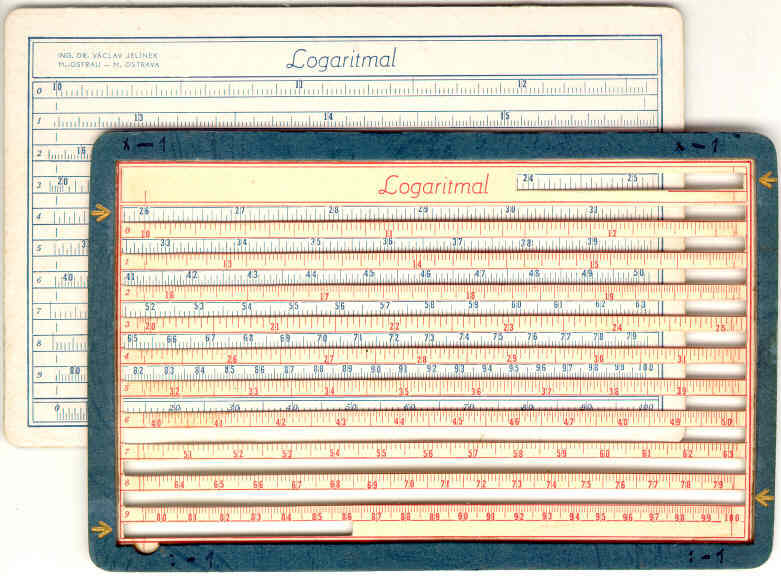
Der Logaritmal trägt kein Produktionsdatum. Auf einem beigefügten kleinen Reklamezettel findet sich eine Schlüsselnummer, die auf -43 endet. Möglicherweise wurde sie im Jahre 1943 gedruckt. Auch eine Anmerkung am Schluss der Anleitung deutet auf kriegsbedingten Materialmangel hin:
"Mangels an anderem geeignetem Material fertigen wir Logaritmal vorläufig aus gutem Papier an. Aus demselben Grunde fertigen wir auch keinen Läufer an. Man kann mit dem Logaritmal ebenso gut ohne Läufer eine Reihe von Rechnungsarten durchführen. Sollte die Interpolation einer weiteren Stelle nötig sein, so kann man sich leicht mit einem durchsichtigen Papier, Zellophan, Zelluloid, Glas usw., auf welchem ein feines Strichelchen (Ritz) angebracht ist, aushelfen."
Hier können Sie einen Scan
(JPEG, ca. 600 KB) herunterladen und
sich selbst einen Logaritmal basteln.
Außerdem gibt es eine lauffähige Demo (ZIP, ca. 600 KB)
für Ihren Bildschirm.
ING. DR. VACLAV JELINEK
Logaritmal
Logarithmisches Rechengerät
in Taschenformat, dessen Genauigkeit
einem logarithmischen Rechenschieber
von 1.5 m Länge entspricht.
Mit dem Logaritmal kann man alle Rechnungsarten höherer Stufen durchführen, vor allem Multiplizieren und Dividieren, Potenzieren und Wurzelziehen, sowie auch andere weitere Rechenaufgaben, welche auf logarithmischer Grundlage basieren.
Logaritmal besteht aus drei Teilen: der Grundplatte, der Zulegeplatte und dem Läufer.
Auf der Grundplatte ist in blauer Farbe eine Zahlenskala (10—100) bezeichnet, welche in 10 gleiche Abschnitte geteilt und auf der linken Seite der Platte mit den Nummern von 0 bis 9 beziffert ist. Außer der Zahlenskala hat die Grundplatte in der letzten, der elften Reihe noch eine logarithmische Skala. Diese logarithmische Skala ist zum Unterschied von der Zahlen-Skala mit schrägen Ziffern bezeichnet.
Auf der Zulegeplatte befindet sich bloß eine Zahlen-Skala, identisch mit der Skala auf der Grundplatte, jedoch der besseren Orientierung halber in roter Farbe bezeichnet. Die Zahlenskala auf der Zulegeplatte hat vier Grundmarken, welche den Anfang und das Ende der Zahlenskala bezeichnen, und zwar so, dass der Anfang von zwei oberen Marken (die linke obere Marke befindet sich über dem 0-ten Abschnitt, die rechte obere Marke im rechten Eck oben) und das Ende von zwei unteren Marken (die linke untere Marke ist unter dem neunten Abschnitt, die rechte untere Marke über dem neunten Abschnitt) angezeigt wird. Diese Anordnung ermöglicht das Rechnen auf einer einzigen logarithmischen Einheit. Die Grundmarken sind genau immer von zwei gegeneinander gezogenen senkrechten Strichen angezeichnet. Zum schnelleren Aufsuchen dienen die an den Seiten der Zulegeplatten befindlichen Pfeile. Zur Durchführung der Berechnung wird die Zulegeplatte so auf die Grundplatte aufgelegt, dass die rote Skala genau parallel in den leeren Reihen unter der blauen Skala erscheint.
Der Läufer ist aus durchsichtigem Material, ähnlich dem Läufer des logarithmischen Rechenschiebers, angefertigt und dient dem genaueren Ablesen, eventuell zur genaueren Interpolation.
Kurze Gebrauchsanweisung des Logaritmals
MULTIPLIZIEREN
Grundregel:
Auf der Grundplatte wird der Multiplikand aufgesucht, auf welchem eine der vier Grundmarken der Zulegeplatte aufgelegt wird, und zwar so, dass der Multiplikand genau zwischen den beiden Strichelchen der Grundmarke der Zulegeplatte zu stehen kommt. Auf der roten Skala wird der Multiplikator aufgesucht. Das Resultat wird genau über dem Multiplikator auf der blauen Skala der Grundplatte abgelesen. Auf den Multiplikand wird stets diejenige der vier Grundmarken aufgelegt, damit sich der Multiplikator auf der roten Skala dann noch im Felde der Grundplatte befindet.
l. 13,4 x 2,74 = 36,72
Multiplikand x Multiplikator = Resultat
Auf der blauen Skala suchen wir den Multiplikand 13,4 (auf dem l. Abschnitt) auf, auf diesen legen wir die obere linke Marke der Zulegeplatte. Auf der roten Skala der Zulegeplatte suchen wir den Multiplikator 2,74 (auf dem 4. Abschnitt) auf und über demselben lesen wir das Resultat auf der blauen Skala der Grundplatte ab. Die Stellung des Dezimalpunktes wird nach der Ordnung des Multiplikanden und Multiplikators bestimmt, genau so wie bei einem gewöhnlichen logarithmischen Rechenschieber.
Ähnlich werden auch weitere Beispiele ausgerechnet.
2. 4,165 x 37,42 = 155,85
Auf den Multiplikand legen wir die linke untere Marke der Zulegeplatte.
3. 0,3133 x 26,72 = 8,372
Auf den Multiplikand legen wir die rechte obere Marke der Zulegeplatte.
4. 606,5 x 0,1744 = 105,77
Auf den Multiplikand legen wir die rechte untere Marke der Zulegeplatte.
DIVISION
Grundregel:
Auf der blauen Skala der Grundplatte suchen wir den Dividend auf, unter welchen wir den auf der roten Skala der Zulegeplatte aufgesuchten Divisor genau anlegen. Das Resultat lesen wir auf der blauen Skala der Grundplatte an der Grundmarke, das ist zwischen den beiden senkrechten roten Strichelchen der Zulegeplatte ab. Zur Geltung kommt immer diejenige von den vier Marken, welche sich im Felde der Grundplatte befindet. Beispiele:
5. 43 : 26 = 1,654
Dividend : Divisor = Resultat
Laut obangeführter Anleitung legt man den Divisor 26 der roten Skala der Zulegeplatte unter den Dividend 43 auf die blaue Skala der Grundplatte. Das Resultat 1,654 lesen wir auf der linken oberen Grundmarke auf auf der blauen Skala ab, wo welches genau zwischen den roten senkrechten Strichelchen aufscheint.
6. 655 : 43 = 15,595
Das Resultat lesen wir an der oberen rechten Marke ab.
7. 13,15 : 0,862 = 152,55
Das Resultat lesen wir an der rechten unteren Marke ab.
8. 18,5 : 35 = 0,5286
Das Resultat lesen wir an der linken unteren Marke ab.
ANDERE HÖHERE RECHNUNGSARTEN
Quadrate rechnet man am schnellsten so aus, dass man die gegebene Zahl mit ihr selbst multipliziert. Ähnlich kann man auch die Kuben berechnen. Man kann auch nach den Regeln für das logarithmische Rechnen vorgehen, was vor allem für das Berechnen von Wurzeln und höheren Potenzen nötig ist.
Logarithmen-Bestimmung:
Die gegebene Zahl suchen wir auf der Zulegeplatte aus, worauf wir die entsprechende Reihe zur logarithmischen Skala auf der Grundplatte so zulegen, dass Anfang und Ende der Reihe sich mit dem Anfang und dem Ende der logarithmischen Skala genau decken. Zu diesem Zwecke ist der Anfang und das Ende einer jeden Reihe auf der Zulegeplatte mit einem kurzen Strich bezeichnet, welcher von der unteren Seite der Reihe führt. Die erste Ziffer der Mantisse ist durch die Reihenfolge gegeben (Bezifferung auf der linken Seite der Platte), die übrigen Ziffern der Mantisse lesen wir auf der logarithmischen Skala ab.
Beispiel 9. Es soll der log. 2,67 bestimmt werden.
Nummer 267 ist in der 4. Reihe, die erste Ziffer der Mantisse ist also 4. Auf der logarithmischen Skala lesen wir den Rest der Mantisse ab: 26,5. Charakteristik = 0.
Resultat: log. 2,67 = 0,4265.
Bei umgekehrtem Vorgange finden wir die Zahl zu dem gegebenen Logarithmus:
Beispiel 10. log. x = 2,1854 Die erste Ziffer der Mantisse ist l, somit ist die gesuchte Zahl in der l. Reihe.
Wir legen also die erste Reihe zur logarithmischen Skala und finden, dass der Rest der Mantisse 85,4 der Zahl 15,325 auf der Zahlenskala entspricht.
Resultat: x = 153,25.
Bei "Illgens-Rechentafel" (hergestellt ca. 1910) ist die Grundplatte vier mal so groß wie die Deckplatte. Dies erleichtert die Multiplikation, vergrößert aber das Gerät.
Rechenwerkzeug.de