Der Soho-Rechenschieber von James Watt

Im 17. und 18. Jahrhundert waren logarithmischen Skalen oft Bestandteil eines Messwerkzeugs für Seeleute, Förster, Steuerbeamte oder andere Praktiker. Für deren jeweiligen Anwendungsbereich waren die Skalen zusammengestellt und mit mit speziellen "Gauge Points" (Markierungen für Konstanten) versehen. Maximale Genauigkeit stand nicht im Vordergrund. Techniker und Konstrukteure, die mit komplizierteren Formeln rechnen mussten, arbeiteten dagegen meist mit der genaueren Logarithmentafel. Erst um 1800 entwarf ►James Watt für die Ingenieure in seiner Maschinenbaufirma mit dem System Soho einen Standard-Rechenschieber mit einfachem Layout, aber sehr exakt gezeichneten Skalen. Den Skalenaufbau übernahm er von Coggeshalls "Timber rule", verzichtete jedoch auf die speziell für Zimmerleute nützliche Verschiebung der D-Skala. Watt bezog die Geräte in Längen von 10 oder 20 Zoll von renommierten Instrumentenbauern in London Später wurden Soho-Rechenschieber auch in Frankreich hergestellt.

Watts Ingenieur und Patentanwalt John Farey liefert in seinem 700-seitigen Buch ►"A Treatise on the Steam Engine" (Buch) nicht nur eine Beschreibung der Dampfmaschine und ihrer Elemente, sondern beschäftigt sich in einem eigenen Kapitel (PDF-Auszug) auf 42 Seiten auch mit Watts Rechenschieber und seiner Anwendung bei Konstruktions- und Rechenaufgaben.

Rechnen mit Logarithmen

Farey definiert den Logarithmus einer Zahl a als diejenige Hochzahl, mit der man 10 potenzieren muss, um a als Ergebnis zu erhalten. Und er erklärt seinen Lesern die Potenz- und Wurzelgesetze: log(a) + log(b) = log(a*b). Wenn man den Logarithmus einer Zahl a und den Logarithmus einer Zahl b addiert, erhält man den Logarithmus des Produkts a * b. Der Logarithmus von 1,8 ist 0,255..., der Logarithmus von 4,2 ist 0,623... Beide Logarithmen addiert ergeben 0,878... Und das ist der Logarithmus von 1,8*4,2, also 7,56.

Anstatt a und b Zahlen zu multiplizieren, kann man also ihre Logarithmen ermitteln, sie addieren und den Logarithmus der Summe delogarithmieren (die dazugehörige Zahl suchen). Anstatt a durch b zu dividieren, kann man ihre Logarithmen subtrahieren und den Logarithmus der Differenz delogarithmieren: log(a) - log(b) = log (a/b). Anstatt die Quadratwurzel aus a zu ziehen, kann man ihren Logarihmus halbieren und das Ergebnis delogarithmieren: log(a)/2 =log(√a).

Zum Logarithmieren und Delogarithmieren benötigt man eine Logarithmentabelle. Die gab es zur Zeit Watts bereits seit fast 200 Jahren Die erste hatte im Jahr 1614 der Schotte John Napier veröffentlicht: "Mirifici Logarithmorum Canonis Descriptio". Kurz darauf hatte der Mathematiker Henry Briggs eine Tabelle der "dekadischen" Logarithmen veröffentlicht. Deren Basis 10 passt zum Dezimalsystem, denn die "Zehnerlogarithmen" von Zahlen mit gleicher Ziffernfolge unterscheiden sich nur in der Vorkommastelle: lg(7,65)=0,878...; lg(76,5)=1,878...; lg(765)=2,878...

Vom Logarithmus zur logarithmischen Skala

Zahlen kann man als Strecken darstellen. Im obigen Beispiel hieße das: Statt 1,8 * 4,2 zu berechnen, zeichnet man eine Strecke von 255 mm und verlängert sie um 623 mm. Dann misst man das Ergebnis: Die gesamte Strecke ist 878 mm lang. Ein Blick in die Logarithmentafel ergibt: Das Ergebnis muss 7,56 oder 75,6 oder 756 ... sein. Wo das Komma hin kommt, muss man durch eine Überschlagsrechnung ermitteln. In diesem Fall hinter die 7.

 

log(3)=0,477

Miithilfe einer logarithmisch geteilten Skala kann man sich das Nachschlagen in einer Logarithmentafel dauerhaft ersparen. Man greift mit einem Stechzirkel den Abstand jedes Skalenstrichs in einem auf drei Stellen genauen Raster ab und markiert ihn auf der Skala. Die Teilstriche beziffert man aber nicht mit den gemessenen Logarithmen, sondern mit den dazugehörigen Zahlen. So erhält man auch nicht den Logarithmus, sondern gleich die Zahl als Ergebnis. Der Logarithmus wird nun nicht mehr in einer Tabelle abgelesen, sondern ist in der Skala versteckt. So entsteht ein Lineal, auf dem der Abstand zweier Zahlen ihrem Verhältnis entspricht: 1 : 3 wie 2 : 6 oder wie 2,7 : 8,1  

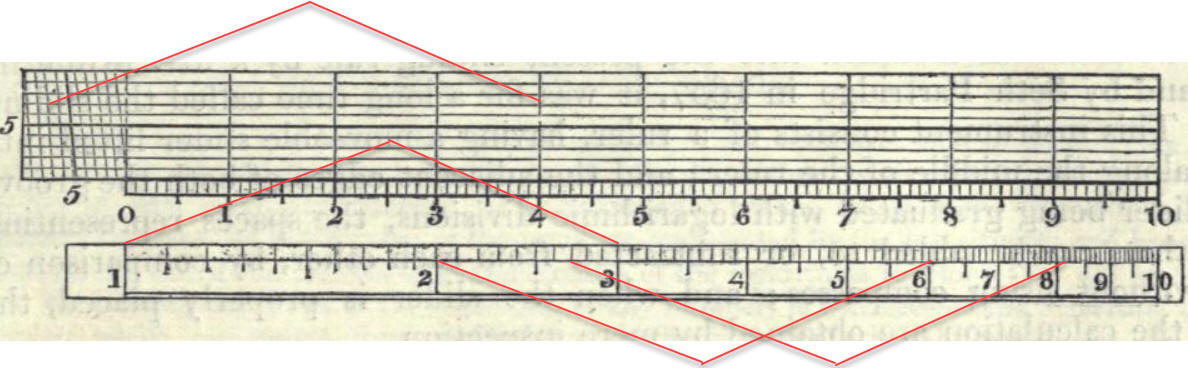
In der oben abgebildeten logarithmischen Skala markiert jeder Teilstrich einen Zuwachs von 0,1. Allerdings werden die Abstände immer enger. Auf der Skala D des Rechenschiebers in der nächsten Abbildung unten werden die Abstände zwischen den Teilstrichen im Bereich zwischen 1 und 2 ihrerseits in jeweils fünf Teile geeilt. Der Zuwachs pro Teilstrich ist hier also 0,02. Zwischen 2 und 10 haben die Teilstriche dann wieder den Abstand 0,1, weil es sonst zu eng werden würde. Dagegen steht auf den Skalen A, B und C, die auf die Hälfte verkürzt sind ein Teilstrich zwischen 1 und 10 immer für die 0,1 und auf der rechten Seite, wo die Nullen von 20, 30, ... bis 100 nur aus Platzgründen weggelassen sind, letztlich für die 1.

Aus zwei Skalenpaaren wird ein Schieber

Das allererste logarithmische Rechengerät war 1624 das Lineal von Gunter, auf dem wie oben dargestellt Verhältnisse mit dem Zirkel abgegriffen und an eine andere Stelle verschoben wurden. Schon ein paar Jahre später fand man es bequemer, den Zirkel wegzulassen und zwei logarithmische Skalen gegeneinander zu verschieben. Das nannte man "Sliding Gunter". Kurz darauf erfand man die Methode, in einen Holzstab ein Bett einzufräsen, in dem man eine Zunge verschieben konnte. So entstand der "Rechenschieber". Um ein derartiges Gerät handelt es sich beim "Soho"-Modell von James Watt. Hier können Sie es ausprobieren. Verschieben Sie einfach den roten Punkt. 

Gerechnet wird bei diesem Modell mit den Skalen A und B. Schieben Sie die 1 der Skala B unter die 2 der Skala A, so steht über der 3 der Skala B die 6 der Skala A: log(2)+log(3)=log(6) oder 2*3=6.  Über jeder Zahl der Skala B steht auf der Skala A der doppelte Wert. Es fällt auf, dass die 20 erneut mit 2 beziffert ist. Tatsächlich ist die rechte Hälfte der Skalen A und B ein exaktes Abblid der jeweils linken Hälfte, nur eben verschoben. Dasselbe gilt für die Logarithmen: War der Zehnerlogarithmus der 1,8  gleich 0,255, so ist der Zehnerlogarithmus der 18 gleich 1,255. In jeder Dekade  wiederholen sich dieselben Nachkommastellen. Die 18 ist von der 10 genauso weit entfernt wie die 1,8 von der 1. Also kann man nicht nur mit den Werten von 1 bis 10, sondern mit allen Zahlen rechnen: Man liest nur die Ziffernfolge aus der Skala ab und setzt das Komma nach einer Überschlagsrechnung.

Dividiert wird übrigens durch Umkehr des Verfahrens: Stellen Sie die 3 der B-Skala unter die 12 der A-Skala, so lesen Sie über der 1 der B-Skala die 4, denn 12 / 3 = 4. Unter der 8 steht jetzt die 2, unter der 20 die 5 ... Alle Zahlenpaare aus einem Wert der A-Skala und dem jeweils darunter stehenden Wert der B-Skala liefern das Divisionsergebnis 4. Man sagt: "Die Zahlenpaare stehen im selben Verhältnis." oder "Sie sind proportional." oder "Sie sind quotientengleich": 8 verhält sich zu 2 wie 20 zu 5.

So lässt sich mit einer einzigen Einstellung eine proportionale Dreisatzaufgabe lösen: Wenn 16 kg Zement 25 Euro kosten, mit welchem Preis muss man dann rechnen, wenn ich 28 kg Zement brauche? Man stellt die 16 über 25 und liest unter der 28 das Ergebnis 45 ab.

Die Skala D  enthält nur eine Dekade von 1 bis 10. Dafür ist sie feiner unterteilt und deshalb auch genauer ablesbar. Beim Soho-Rechenschieber dient sie zum Quadrieren und Wurzelziehen. Wenn man die 4 der Skala A durch einen beliebigen Teilstrich mit der Skala D verbindet, liest man am unteren Ende des Strichs die Quadratwurzel der 4 ab. Genau unter der 9 steht die 3, genau unter der 36 die 6. Die 36 ist die  3,6 auf der rechten Seite. Die Wurzel aus 3,6 (linke Seite) ist nicht 0,6, sondern etwa 1,9. Von unten nach oben wird quadriert. Genau über der 5 der D-Skala kann man auf der A-Skala 2,5 ablesen. Hier bedeutet das 25.

Die Inversskala

Es muss ein Spielkind gewesen sein, das versuchsweise einmal die Zunge verkehrt herum in den Rechenschieber gesteckt hat. Dabei fiel ihm auf: Wenn man auch die Rechenanleitungen für Multiplation und Division vertauscht, dann passt es wieder.

Stellen Sie die 3 der B-Skala unter die 15 der A-Skala, so findet sich die 10 unter der 4,5 (gelesen als 45). Galt in der Normalstellung der Zunge: Paare aus übereinanderstehenden Werten sind quotientengleich, so gilt bei Inversstellung der Zunge: Paare aus übereinander stehenden Werten sind produktgleich. Auch 5*9 ergibt 45 ebenso wie 6*7,5.

Das fand man so praktisch, dass einige Intrumentenmacher Rechenschieber mit zwei Zungen anboten. Da man bei den Soho-Rechenschiebern die Zunge nicht mit der Rückseite nach oben einstecken konnte - baute man die Körper doppelt so dick und verlegte die zweite - rückläufige - Zunge auf der Rückseite des Körpers .

Bei Inversstellung der Skala kann man antiproportionale Dreisatzaufgaben mit einer Einstellung lösen: Wenn man einen Balken mit einem Querschnitt von 35 cm Breite und 16 cm Dicke durch einen Balken von 25 cm Breite mit gleicher Tragkraft ersetzen muss, wie dick sollte dieser dann sein? Man stellt die 16 unter die 35 und liest unter der 25 die 22 ab. (Die Skalenbilder sind ein wenig ungenau.).

Gefaltete Skalen

Nichts ist so gut, dass man es nicht verbessern kann. Die A-Skala mit zwei Dekaden lässt sich nur halb so genau ablesen wie die D-Skala, die nur eine Dekade hat. Indem man die B-/C-Skala der Zunge analog zur D-Skale nur einmal von 1 bis 10 laufen lässt, kann man die Ablesegenauigkeit verbessern. Multiplizert und dividiert wird also jetzt mit C und D.

Manche Ergebisse - etwa das der Rerchnung 3*4 - werden nun jedoch  außerhalb der D-Skala angezeigt. Man müsste in solchen Fällen nicht die 1, sondern die 10 über die 3 stellen - das nennt man "Durchschieben" - und könnte das Ergebnis 12 als 1,2 unter der 4 ablesen. Oft weiß man allerdings vor der Rechnung nicht, ob man durchschieben muss oder nicht. 

Vielleicht war es praktischer, die 1 in die Mitte zu verschieben. Wenn nun das Ergebnis außerhalb der Skala lag - etwa bei 2,7 * 2,8 , brauchte er nicht mehr die Zunge durchzuschieben, sondern nur die Faktoren zu vertauschen, um 2,8 * 2,7. Das Ergebnis fand sich immer unter der 1. Allerdings musste er nun beim Divieren manchmal durchschieben oder die Zunge wenden.

Schon Coggeshall hatte in die mit einem Zollstock kombinierten Rechenstäbe eine um 4 verschobene "Girt Line" integriert. Bei Fareys ersten verbesserten Soho-Rechenstäben war die D-Skala so wie hier um 3 versetzt und außerdem invertiert. Bei Rechenstäben späterer Generationen waren gefaltete Skalen oft als Option erhältlich. Eine Normalskala kombiniert mit einer um Pi gefalteten Skala, ersparte Einstellungen bei Kreis- und Kugelberechnungen. Eine normale Skala, kombiniert mit einer inversen und einer um 3,60 gefalteten Skala ermöglichte die Berechnung taggenauer Zinsen mit einer einmaligen Platzierung der Zunge.

Weitere Skalensysteme

Farey experimentierte weiter: Er setzte die inverse und gefaltete Skala B nach unten und die Skala D auf die Zunge. Nun konnte er mit dem unteren Skalenpaar multiplizieren und dividieren und mit dem oberen Skalenpaar Quadrate und Wurzeln bestimmen.

Außerdem schlug er vor, die Zunge mit symmetrischem Querschnitt zu bauen, sodass man sie auch mit der Rückseite nach oben einsetzen konnte. Dort brachte er zwei weitere Skalen an, die jeweils mit der invertierten und gefalteten B-Skala zusammenarbeiten: Eine E-Skala, die direkt vom Volumen in die Oberfläche einer Kugel  umrechnete, indem sie den Wert der B-Skala mit 3 potenzierte und daraus die Wurzel zog. Außerdem die invertierte Mantissensskala N. Die Rückseite des Körpers belegte er mit Tabellen. Viele Möglichkeiten also bei komplizierter Handhabung. Ob dieser Skalenaufbau jemals realisiert wurde, ist nicht sicher.

►Alle Varianten in einer Animation

Ein Soldat räumt auf

Viele Rechenschieber kamen mittlerweile aus der Werkstatt von Lenoir in Paris, der mit einer neue Skalenteilungsmaschine die Serienfertigung von Mess- und Rechengeräten revolutioniert und gleichzeitig die Genauigkeit gesteigert hatte. Für Lenoirs Nachfolger Tavernier-Gravet entwarf der französische Armeeleutnant und Mathematiker Amédée Mannheim im Jahr 1851 ein Rechenschieber-Layout. Er übernahm die Ideen mit der Wendezunge und der Mantissenskala und fügte auch die von Watt als entbehrlich erachteten Sinus- und Tangensskalen wieder hinzu. Weil er außerdem den Rechenschieber durch einen Läufer erweiterte und in die Unterseite des Körpers Ablesefenster für die Rückseite einfräsen ließ, war es nun möglich, die Werte in einer Rechnung beliebiger Skalen zu kombinieren. Mannheim verzichtete weitgehend auf extra markierte "GaugePoints" in den Skalen und füllte stattdessen die Rückseite mit Konstantentabellen. Und er gewann sogar Platz, um auf seinem Rechenschieber noch eine Zentimeterskala zum Messen und Zeichnen unterzubringen.

Fotos aus Collecting Slide Rules Beginner's Guide von Ted Hume und Rod Lovett auf oughtred.org

Rechenwerkzeug.de