Die Tyler-Rechenscheibe

John Tyler war Professor für Mathematik an der US Marineakademie in Annapolis Maryland. Im Jahre 1919 wurde er zum Associate Professor ernannt, auch 1949 wurde er im Jahrbuch der Marineakademie noch als Professor geführt.

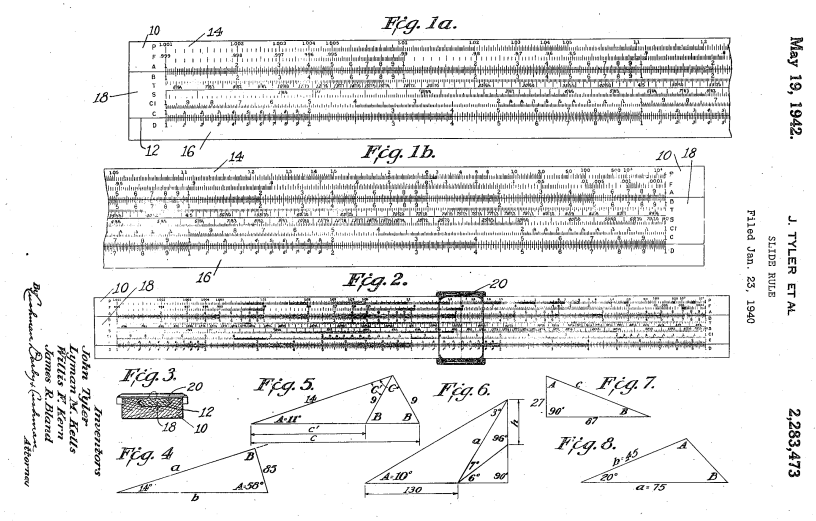
Das US Patent Office erteilte John Tyler (und drei Kollegen) 1942 das Patent 2283473 für einen verbesserten Rechenschieber nach dem Mannheim-Skalensystem: ein einseitiges Gerät, 16 Zoll lang, die A- und B-Skala erstrecken sich über vier, die C- und D-Skala über zwei Größenordnungen und die sonst häufig gedrittelte Log-Log-Skala ist in einem Stück vorhanden. So kann die Zahl der Skalen von 20 auf 9 reduziert werden, ein Umdrehen der Zunge ist überflüssig und viele Rechnungen können ohne "Durchschieben" und mit insgesamt weniger Einstellarbeit ausgeführt werden. Der Rechenschieber wurde von Keuffel und Esser als Modell 4110 vertrieben und ist hier und hier beschrieben. Er erreichte aber wohl keine großen Auflagen und war auch nicht in allen Katalogen von K+E enthalten.

Die exotische Tyler Rechenscheibe

Nach seiner Emeritierung entwarf John Tyler ein weiteres Rechengerät, das in den fünfziger Jahren von der Firma Weems System of Navigation vertrieben wurde und wohl vor allem in der Ausbildung eingesetzt werden sollte. Auch diese Rechenscheibe wurde zum Patent angemeldet, dieses wurde aber offenbar nie erteilt. Die logarithmische Skala ist auf dieser Scheibe nur einfach vorhanden, und zwar in Form einer ca. 30 cm. langen Spirale, die, weil sie von innen nach außen aufgetragen ist, die großen Abstände im unteren Bereich der logarithmischen Skala staucht und die kleinen Abstände im oberen Bereich dehnt und so die bei Rechenscheibern nach oben hin abnehmende Ablesegenauigkeit ausgleicht.

Die Spiralskala befindet sich drehbar auf einer transparenten Folie, darunter sind auf der Grundplatte sechs Funktionsgraphen sichtbar, über die die Werte der Skala eingestellt und abgelesen werden. Für Multiplikations- und Divisionsaufgaben gibt es einen festen Index auf der Grundplatte und einen beweglichen Index als Läufer. Die übrigen Funktionen (Wurzelziehen, natürlicher Logarithmus, Sinus und Tangens) werden am festen Index eingestellt und am Schnittpunkt des jeweiligen Funktionsgraphen mit der logarithmischen Skala abgelesen.

 

Rodger Shepherd widmete der Rechenscheibe im Jahr 2000 eine auführliche Betrachtung im Journal der Oughtred Society (die von Peter Abramson im Folgejahr in einem Leserbrief um einige weitere Informationen ergänzt wurde). Shepherd erkennt die Originalität des Konzepts an, bemängelt jedoch Genauigkeitsverluste durch den teilweise schwer exakt zu bestimmenden Schnittpunkt der Indexlinien mit der Spiralskala.

Als ich eine solche Scheibe bei Ebay entdeckte, hielt ich sie zu erst für ein Nomogramm für irgendeine spezielle Anwendung. Erst bei näherem Hinsehen, entdeckte ich, dass es sich um eine universelle Rechenscheibe handelte. Der emeritierte Mathematikprofessor Tyler hielt sie für einfacher in der Handhabung als die üblichen Rechenschieber.

Während ich meinen Etat noch prüfte, war das exotische Gerät schon weg. Eine kurze Recherche bei http://sliderules.lovett.com/srsearch.html ergab: Die Scheibe erreichte offenbar keine große Verbreitung, bei Ebay wurde sie in all den Jahren gerade 15 mal angeboten - allerdings mit erheblichem Aufschlag gegenüber dem seinerzeit geforderten Preis von 6 Dollar.

Dass Tylers Rechenscheibe in überschaubarer Zukunft wieder bei Ebay auftauchen würde, schien mir unwahrscheinlich. So trieb ich schließlich eine qualitativ gute Abbildung der Scheibe auf und zerlegte diese per Photoshop in ihre beiden Ebenen: die Grundscheibe mit festem Index und Funktionsskalen und das Overlay mit der logarithmischen Spirale und der kreisförmigen Zehnerlogarithmusskala. Daraus erstellte ich eine Animation und einen Nachbau der Scheibe.

Wenn Sie wollen, können Sie jetzt die Rechenscheibe anhand einer Animation ausprobieren.

Sind Sie jedoch mehr der haptische Typ und suchen ein neues Glanzstück für Ihre Sammlung,
dann besorgen Sie sich eine Schaumstoffplatte, eine Overheadfolie und eine Heftzwecke und drucken Sie sich den folgenden Bausatz aus (Download als ZIP).

Ich wünsche viel Spaß.

Hier die Übersetzung der Original-Dokumentation:

TYLER RECHENSCHEIBE
Ein neues Konzept, das unter Verwendung von Indexkurven mit einer Skala auskommt. Entworfen von John Tyler, emeritierter Professor für Mathematik an der US Marineakademie. Hergestellt von Weems Navigationssysteme. 6 $

DIE TYLER-RECHENSCHEIBE

Die Tyler-Rechenscheibe ist einzigartig im Konzept und sehr originell im Design. Bei der ersten Inspektion fällt vor allem das übersichtliche Layout auf: Im Gegensatz zu den meisten Rechenschiebern ist nur eine nummerierte Skala erforderlich, um sowohl mathematische als auch trigonometrische Probleme schnell lösen zu können. Diese Skala hat die Form einer Spirale mit zunehmender Steigung, ein Design, das die Skala in ihrem oberen Bereich, wenn sie sich 10 nähert,  stark erweitertund sie dem herkömmlichen Rechenschieber weit überlegen macht.

Die Tyler-Scheibe hat viele Vorteile gegenüber dem herkömmlichen Rechenschieber. Sie ist flach und dünn und kann in einem Buch aufbewahrt werden. Sie hat nur eine einzelne statt einer Vielzahl von nummerierten Skalen, was ihre Verwendung erheblich vereinfacht. Die Interpolation ist auf dieser Skala immer gleich, unabhängig davon, welches Problem gelöst wird. Die Tyler-Scheibe hat eine einheitliche Methode zur Lösung aller Probleme, die der Mathematiker als Verhältnis angibt. Für diejenigen, die in Bezug auf Multiplikation und Division denken, gilt eine Grundregel für alle Berechnungen: Drehen Sie die Scheibe, um zu multiplizieren, und drehen Sie den Läufer, um zu dividieren.

Die Tyler-Scheibe besteht aus drei Komponenten: einer festen Basis, einer drehbaren durchsichtigen Scheibe und einem drehbaren Läufer. Auf der festen Basis sind ein radiale Indexlinie (schwarzer Index) sowie sechs gekrümmte Indexlinien markiert. Letztere haben keine nummerierten Skalen, sind aber zur Identifizierung beschriftet. Der A-Index wird zur Bestimmung von Quadraten und Quadratwurzeln verwendet. Die S- und T-Indizes werden zur Bestimmung des Wertes von Sinus und Tangens von Winkeln größer als 10° verwendet S₂ und T₂ für Winkel kleiner als 10°. Die ln-Skala wird zur Bestimmung der Potenzen von e verwendet.

Die drehbare Scheibe trägt die spiralförmige C-Skala, die bei allen Berechnungen verwendet wird. Diese Skala ist innen von 1 bis 10 und außen von 10 bis 100 schwarz nummeriert. Sie ist auch umgekehrt in roten Ziffern nummeriert, um sie mit Winkelfunktionen zu verwenden. Am äußeren Rand der Scheibe wird auch eine Skala von 0 bis 10 angezeigt, um die Logarithmen der Zahlen zu bestimmen.

Der Läufer ist transparent und mit einer rot gefärbten Haarlinie (roter Index) versehen.

Wir glauben, dass diese Scheibe durch ihren einfachen Aufbau für Schüler geeignet ist. Ihre Bequemlichkeit und die Tatsache, dass sie überall auf der Skala leicht auf drei Stellen genau abgelesen werden kann, wird sie ebenso dem Ingenieur und Wissenschaftler empfehlen.

GEBRAUCHSANWEISUNG FÜR DIE TYLER-RECHENSCHEIBE

Die Tyler-Rechenscheibe besteht aus drei Teilen: (1) einer Grundplatte, auf der eine gerade schwarze Indexlinie und eine Vielzahl gekrümmter Indexlinien aufgedruckt sind, die entsprechend ihrer jeweiligen Funktion benannt sind. (2) eine runde transparente Auflage, auf der sich eine Spiralkurve (C) befindet, die für alle Berechnungen verwendet wird. Die Zahlen im Inneren der Spirale werden bei  Berechnungen mit Zahlen verwendet, die Zahlen außerhalb der Spirale in Schwarz und Rot werden für Winkelfunktionen verwendet. Die L-Skala befindet sich auf dem Umfang der transparenten Scheibe als Referenz und wird verwendet, um die Zehnerlogarithmen von Zahlen zu bestimmen. (3) Ein transparenter Cursor, auf dem sich eine gerade rote Indexlinie befindet.

PROPORTIONEN VON ZAHLEN - Beispiel: Das Verhältnis 3:4. Drehen Sie die 3 der C-Skala (Auflage) auf den schwarzen Index (Grundplatte) und dann den roten Index (Läufer) auf 4 der C-Skala. Fixieren Sie mit dem Daumen das äußerste Ende des Läufers auf der Grundplatte. Wenn nun die Spirale gedreht wird, stehen alle Paare von Zahlen, durch die die beiden Indexlinien verlaufen im Verhältnis 3:4. Wenn die C-Skala so eingestellt ist, dass 8 beim roten Index erscheint, dann liegt die 6 beim schwarzen Index. Das Verhältnis 3:4 = 6:8 usw.

MULTIPLIKATION UND DIVISION - Solche Aufgaben können als Proportionen betrachtet werden. Wenn Sie sie als Multiplikation und Division betrachten, drehen Sie immer die transparente Scheibe, um zu multiplizieren, und den Läufer, um zu dividieren. Dies ist die einzige Regel, die Sie beachten müssen. Stellen Sie die beiden gegebenen Zahlen ein, drehen Sie den Läufer oder die Skala und lesen Sie das Ergebnis am schwarzen Index ab.

Beispiel: Multiplizieren Sie 4,32 x 5,75. Stellen Sie beim schwarzen Index 4,32 ein. Stellen Sie den roten Index auf 1. Drehen Sie die 5,75 der C-Skala unter den roten Index und lesen Sie das Produkt 24,8 beim schwarzen Index ab. Die Schritte sind 4,32 : 1 x 5,75.

Beispiel: Teilen Sie 7,85 durch 3,4. Setzen Sie 7,85 auf den schwarzen Index, setzen Sie dann den roten Index auf 3,40. Drehen Sie dann 1 unter den roten Index und lesen Sie die Antwort 2,31 beim  schwarzen Index ab. Als Proportion liest sich das so: 7,85 : 3,4 = 2,31 : 1

Um 6 : 3 x 5 zu berechnen, setzen Sie 6 an den schwarzen Index, setzen den roten Index auf 3 fixieren den Läufer mit dem Daumen auf der Grundplatte dund drehen die Scheibe bis die 6 beim roten Index ist. Am schwarzen Index können Sie dann das Ergebnis 10 ablesen.

QUADRATE UND QUADRATWURZELN - Verwenden Sie den gekrümmten Index A und den schwarzen Index.

Beispiel: Finden Sie die Quadratwurzel von 4. Bringen Sie 4 zum schwarzen Index und lesen Sie die Antwort 2 an der Stelle, an der der A-Index die C-Skala schneidet. Die Quadratwurzel von 40, nämlich 6,32 befindet sich genau gegenüber am anderen Schnittpunkt von A und der C-Skala.

Wenn Quadrate in einer Formel vorkommen, ist die Einstellung 3 im A-Index identisch mit der Einstellung 3² oder 9 auf dem schwarzen Index. Dieses Prinzip gilt für alle gekrümmten Indexlinien.

WINKELFUNKTIONEN - Die gekrümmten Indizes S und T werden für Sinus- und Tangenswerte von Winkeln größer als 10° verwendet, S₂ und T₂ für Winkel von weniger als 10°. Die entsprechenden Winkel stehen als schwarze oder rote Zahlen außerhalb der Skala: schwarze Zahlen zum Einstellen von Sinus und Tangens, roten Zahlen zum Einstellen von Cosinus und Cotangens. Beispiel: Wenn Sie 30° auf den S-Index setzen, so werden Sie feststellen, dass 0,5, der Sinus von 30°, auf dem schwarzen Index liegt.

Setzen Sie den T-Index auf 36° und lesen Sie 0,727, den Tangens von 36° beim schwarzen Index. Der Tangens von 62° ist 1,88 usw. Setzen Sie den S-Index auf Rot 15° und lesen Sie 0,955 als Cosinus von 15° beim schwarzen Index ab. Setzen Sie T₂ auf 3° (an diesem Punkt sind T₂ und S₂ identisch) und lesen Sie 0,0524 den Tangens von 3° beim schwarzen Index ab.

Um den Winkel zu finden, dessen Sinus 0,634 ist, setzen Sie 0,634 auf den schwarzen Index und lesen Sie 39,3° am S-Index ab. Um den Winkel zu finden, dessen Tangens 0,334 ist, stellen Sie 0,334 beim schwarzer Index ein und lesen Sie 21° beim T-Index ab. Der Tangens von 45° ist 1, und sein Punkt ist auf dem T-Index markiert, um Sie darauf hinzuweisen, welchen Abschnitt des T-Index Sie benutzen müssen, wenn der T-Indes die C-Skala zweimal schneidet.

FORMELN MIT WINKELFUNKTIONEN (als Proportionen geschrieben) - Bestimmen Sie X für sin 25° : 6,25 = sin X : 7,5 - Setzen Sie 25° auf den S-Index, setzen Sie den roten Index auf 6,25. Drehen Sie die Scheibe, sodass 7,5 beim roten Index steht, und lesen Sie die Antwort X = 30,4° am S-Index.

Bestimmen Sie A für tan A : sin 30° = tan 62° : sin 45° - Verwenden Sie den S-Index und den schwarzen Index und bestimmen Sie den Sinus von 30° und 45° und Vereinfachen Sie die Gleichung zu tan A : 0,5 = tan 62 : 0,707. Setzen Sie den T-Index auf 62° und den roten Index auf 0,707. Drehen Sie die Scheibe, bis 0,5 beim roten Index steht und lesen Sie A = 53° beim T-Index ab.

LOGARITHMEN - Gegenüber N auf der C-Skala lesen Sie Log N auf der L-Skala. Dies ist die Mantisse des Zehnerlogarithmus. Beispiel: Finden Sie den Logarithmus von 4,09. Gegenüber 4,09 auf der C-Skala lesen Sie das Ergebnis 0,612 auf der L-Skala ab.

Potenzen von e: Für Exponenten von e^0,23 bis e^2,3 setzen Sie den Exponenten auf den schwarzen Index und lesen Sie die Zahl auf dem In-Index ab. Beispiel: e^1,9 = 6,68. Um Zahlen zu erhalten, die Potenzen von e darstellen, die nicht innerhalb der oben genannten Grenzen liegen, verwenden Sie Teile des Exponenten und multiplizieren Sie. Beispiel e³: Bestimmen Sie wie oben e^1,5 = 4,48 und quadrieren Sie, um 20,1 zu erhalten. Oder verwenden Sie e² = 7,39 und e = 2,72, multiplizieren Sie 7,39 x 2,72, um e³ = 2,0: 1 zu erhalten.

Als Proportion betrachtet: Wenn N = e^x, dann log N : x = log e : 1 

Potenzen von Zahlen können mit der gleichen Proportionsmethode ermittelt werden, Beispiel N = 5³: log N : 3 = log 5 : 1 Gegenüber 5 der C-Skala lesen Sie log 5 = 0,699 auf der L-Skala ab.  Ersetzen Sie log 5 in der Formel durch 0,699 und lösen Sie mit dem roten und schwarzen Index. Log N = 2,1 und die Mantisse ist 0,1. Gegenüber 0,1 auf der L-Skala lesen Sie 1,25 auf der C-Skala. Durch eine Kommaverschiebung um 2 Stellen erhalten Sie 5³ = 125.

Zum Lösen von ln N = n. Beispiel: Finden Sie ln 2. Setzen Sie den ln-Index auf 2 der C-Skala und lesen Sie das Ergebnis 0,693 beim schwarzen Index ab.

Rechenwerkzeug.de