Teilbarkeitskarte
Ein Lernmittel zu den Kriterien
der Teilbarkeit, vom Bildungsministerium empfohlen
Editione Baldamenti Via Locatelli 7 Bergamo
Zweifarbige Ausführung 1000 Lire in ganz Italien
VORTEILE DER «TEILBARKEITSKARTE VON BADALAMENTI»
Mit der Einführung der «Teilbarkeitskarte» in
Mittel-, Anfänger- und Pflichtschulen (erste, zweite und dritte Klasse)
haben Sie folgende Vorteile:
1 – Die Teilbarkeitskarte
beseitigt Lernhindernisse. Der Mathematikunterricht lehrte bisher die Kriterien der Teilbarkeit durch 2, 3, 5, 11, um die Zerlegung in Primfaktoren zu erleichtern, aber es ging
nicht über diese Teiler hinaus, weil es an Teilbarkeitskriterien mangelte, die
Kindern zugänglich waren. Nachdem Gaetano Badalamenti dieses allgemeine
Teilbarkeitsschema entdeckt hat, hat er es in einer klaren und einfach zu
verwendenden mechanischen Form angepasst und die hier vorgestellte
doppelseitige Tafel entworfen. Wir können also zum Nutzen des
Mathematikstudiums auf Teilbarkeitskriterien für die Zahlen 3, 5, 7, 11, 13, 17,
19, 23, 29. 31, 37, 41, 43 zurückgreifen.
2 – Sie ermöglicht den Schülern, viele
Operationen an Brüchen in viel kürzerer Zeit als bisher
durchzuführen, da die Zeitverschwendung der vielen
nutzlosen Unterteilungen, die durchgeführt werden mussten, um nach dem
Faktor zu suchen, wenn die bereits bekannten Kriterien für 2, 3, 5, 11 nicht
ausreichten, vollständig beseitigt wird.
3 - Sie ist nützlich, um Mathematik zu lernen,
da Sie anstelle von 5 oder 6 Zerlegungsübungen von Hand mit dem Lineal
mindestens 15 oder 20 in kürzerer Zeit ausführen können.
4 – Ihre Verwendung hilft Fehler zu vermeiden.
5 – Sie ermöglicht die Verwendung eines
Präzisionsinstruments schon in den frühesten Klassen.
6 – Sie erspart die Suche in Primzahltabellen,
da diese auf dem Lineal direkt angegeben sind.
7 – Der Lehrer kann problemlos jede Übung
aufgeben, ohne zuvor zumutbare Nenner berechnen zu müssen. Tatsächlich
zerlegt das Lineal alle Zahlen bis zu 6400 (ungerade bis zu 3199).
I – THEORIE
Die "Karte zur Teilbarkeit von Zahlen" basiert
auf einer Theorie, die der italienische Mathematiker Gaetano Badalamenti
1957 entdeckte. Damals befassten sich das italienische Radio und die
italienische Presse damit. Kürzlich wurde der Erfinder von Radio
Monteceneri, dem Schweizer Fernsehen und mehreren ausländischen Zeitungen
interviewt. Die Theorie wird durch das italienische Industriepatent Nummer
572650 geschützt und das eigentliche Werkzeug mit dem italienischen Patent
Nummer 593077.
Im Ausland ist die Karte in den Hauptnationen
durch ebenso viele Patente geschützt.
1962 gewann der Erfinder auf der XI.
Internationalen Ausstellung für Erfindungen in Brüssel die einzige
Goldmedaille von siebzehn teilnehmenden Nationen in der Kategorie
"Bildungsinstrumente".
II – ANWENDUNG
Wir wissen, dass die Mathematik uns lehrt, die
Teilbarkeit einer Zahl anhand der seit langem bekannten
Teilbarkeitskriterien für 2, 3, 5, 11 und für die Quadrate oder oder dritten
Potenzen dieser Zahlen festzustellen.
Über 11 hinaus gibt es keine einfach
anzuwendenden Teilbarkeitsregeln, und man muss durch Ausprobieren fortfahren und für
jeden Test eine vollständige Unterteilung durchführen. Das
Verfahren ist langwierig, nervig und fehleranfällig, so dass es den Schüler
zum Nachteil des Themas irritiert.
Unsere Teilbarkeitskarte beseitigt diese
Nachteile und zeigt sofort an, ob eine Zahl teilbar oder eine
Primzahl ist. Im Fall der Teilbarkeit gibt sie alle Faktoren, d. h. die
Primzahlen, durch die sie geteilt werden können, gleichzeitig an. Sie weist
jedoch nur auf die erste Potenz hin, das heißt, es gibt nicht die
vollständige Zerlegung. Dies stellt ein allgemeines Teilbarkeitskriterium
bis 43 (durch 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43) dar. Das
ist mehr als genug für den normalen Schulgebrauch.
Die Faktoren erscheinen in der ersten Potenz,
da es antididaktisch wäre, wenn die Regel die vollständige Aufschlüsselung
geben würde, die für die Schüler der Mittelschule und den guten Willen
bestimmt ist, die dieses Verfahren lernen müssen. Von jeder in der Regel
markierten Zahl finden wir daher alle angegebenen Primfaktoren, d.h. alle
Teiler, die kleiner als 47 sind. Wenn die Zahl andere Teiler hat, ergeben
sich diese aus der Zerlegung, aber sie sind sicherlich größer als 43.
Die Teilbarkeitskarte ermöglicht so Berechnungen mit Brüchen, Summe
und Differenz zweier Brüche, Reduktion auf die minimalen Terme, d.h. es
hilft auf der Suche nach dem maximalen gemeinsamen Teiler und dem minimalen
gemeinsamen Vielfachen.
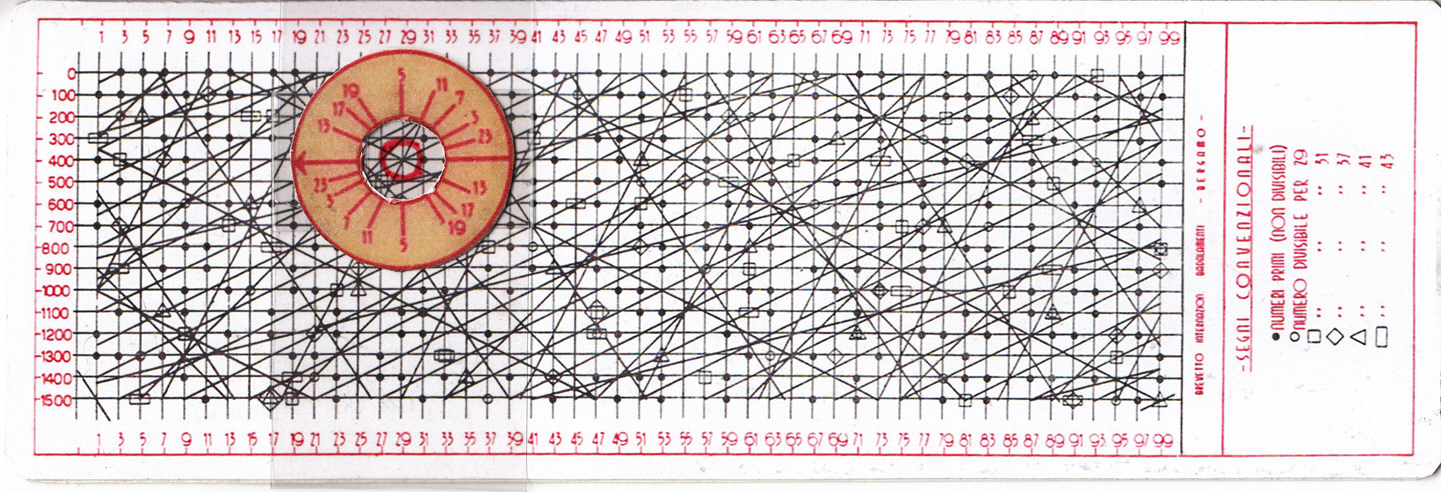
III – DIE TEILE DES INSTRUMENTS
Das komplette Instrument ist in drei Teile unterteilt:
Läufer, Winkelmesser und die eigentliche Teilbarkeitskarte.
LÄUFER aus transparentem
Material – Er ist horizontal verschiebbar und hat zwei kleine vertikale
Hilfslinien, die zur Einstellung auf den Zehner und Einer auf der oberen
oder unteren Skala oder verwendet werden.
WINKELMESSER aus bedrucktem
transparentem Material - Es ist vertikal verschiebbar und hat eine
ringförmige Krone, auf der kleine Segmente markiert sind, die alle auf die
Mitte der Anzeige gerichtet und mit den Primzahlen von 3 bis 23 markiert
sind. Sie werden verwendet, um die geraden geneigten Linien zu
identifizieren, die das Lineal füllen. Auf der linken Seite befindet sich
außerdem ein Pfeil, der auf die Hunderter der zu zerlegenden Zahlen
gerichtet ist.
TEILBARKEITSKARTE beidseitig bedruckt:
– a) dichte vertikale Hilfslinien – b) ebenso dichte
horizontale Hilfslinien – c) ein Netzwerk geneigter Linien,
unterteilt in große Gruppen von Parallelen mit unterschiedlichen
Neigungswinkeln – d) viele Punkte und andere Zeichen in Form
geometrischer Figuren. Auf der rechten Seite befindet sich die Legende für
die Punkte und die geometrischen Figuren.
Die horizontalen Linien
repräsentieren die Hunderter. Jede Linie repräsentiert die Hundert, die am
Anfang der Linie am linken Rand des Lineals stehen.
Vertikale Linien repräsentieren die Zahlen von 1 bis 99. Jede Linie repräsentiert die Zahl, die sie auf der oberen und unteren Skala berührt.
Die geneigten Linien stellen die
Faktoren von 3 bis 23 dar und werden an den Segmenten des Winkelmessers
abgelesen.
Diejenigen vertikalen Linien, die durch
Vielfache von 5 verlaufen stellen Faktor 5 dar.
Die geometrischen Figuren
symbolisieren Faktoren, die in der Legende auf der rechten Seite der Karte
angegeben sind.
Punkte markieren die
Primzahlen von 1 bis 3199 dar und ersetzen eine Tabelle der Primzahlen.
Kreuzungen horizontaler und vertikaler Linien: Jede Kreuzung einer horizontalen Linie mit einer vertikalen Linie entspricht einer Zahl, die der Summe der durch die horizontale Linie angegebenen Hunderte und der durch die vertikale Linie angegebenen Zehner und Einheiten entspricht. Der Schnittpunkt ist daher die Zahl, die wir in Primfaktoren umwandeln möchten. Die herkömmlichen Linien und Zeichen, die exakt über die Kreuzung verlaufen (und nur diese), sind die Faktoren.
Beispiel:
....... 25 27 29 31
300 |
400
----------|-------
500 |
Der Kreuzungspunkt dieser beiden Linien
repräsentiert die zu zerlegende Zahl 429.
GEBRAUCHSANWEISUNG
1 - Lassen Sie die Zahl 523 in Faktoren
zerlegen: Bewegen Sie den Läufer nach links und bewegen Sie
den Winkelmesser nach oben oder unten, bis der Pfeil mit der Linie
übereinstimmt, die aus der 500 herauskommt. Lassen Sie nun den Winkelmesser
in seiner Position. In dieser Zeile bewegen wir den Läufer nach rechts, bis
die obere und untere Hilfslinie die Zeile berühren, die aus Nummer 23 auf
der oberen oder unteren Skala hervorgeht. In der Mitte des Winkelmessers
sehen wir den Schnittpunkt der beiden Linien, die aus der 500 und die aus
der 23 hervorgeht. Diese Kreuzung ist daher dieT 523. Auf dieser Kreuzung
befindet sich ein Punkt. Die Legende rechts neben dem Nomogramm
zeigt an,
dass der schwarze Punkt bedeutet, dass 523 eine Primzahl ist.
2 - Lassen Sie die Zahl 519 in Faktoren
zerlegen: Suchen Sie links nach 500, stellen Sie den Pfeil
des Winkelmessers daneben und bewegen Sie den Läufer, bis die Hilfslinie die
Zahl 19 berührt. An der Kreuzung, die 519 darstellt, sehen wir eine geneigte
Linie, die mit der auf dem Winkelmesser markierten Nummer 3
übereinstimmt. Nehmen wir an, 519 ist durch 3 teilbar und hat keine anderen
Faktoren als 47. Andernfalls würde der Regulus sie anzeigen. Hinweis - Die
Faktoren einer Zahl sind die Linien und herkömmlichen Zeichen, die der
Kreuzung überlagert sind, und nur diese. Die Linien und benachbarten Zeichen
wirken sich nicht auf die Zahl aus, die wir aufteilen.
3 - Lassen Sie uns die Nummer 589
aufschlüsseln: Mit dem Pfeil des Winkelmessers, den wir
nach links zurückbewegt haben, berühren wir die 500, und mit der Hilfslinie
laufen wir, um die Nummer 89 zu berühren, ohne den Winkelmesser von der
horizontale Linie von 500 wegzubewegen. Am Schnittpunkt der Linien in der
Mitte des Winkelmessers lesen wir die Faktoren von 589. Tatsächlich gibt
es es ist eine geneigte Linie, die mit der Winkellinien der roten 19
zusammenfällt und im Schnittpunkt ein Quadrat. Bedeutung: 589 ist durch 19
und 31 teilbar und hat keine anderen Faktoren bis 47.
Hinweis: Wir haben es in
diesem Fall vermieden zu beweisen, ob die Zahl 589 durch 3, 5, 7, 11, 13,
17, 19 teilbar ist oder nicht, wodurch eine Reihe völlig nutzloser
Unterteilungen eingespart werden.
4 - Lassen Sie die Zahl 1763 aufschlüsseln:
Wir nehmen den Läufer ab, wenden die Karte und setzen den Läufer wieder
ein. Der Pfeil muss auf 1700 und die Einstellinie 63 gebracht werden, die
auf der unteren Skala besser lesbar ist, da die obere vom Winkelmesser
abgedeckt bleibt. Am Schnittpunkt der Linien 1700 und 63 finden wir ein
Dreieck und ein Rechteck. Bedeutung: 1763 ist teilbar durch 41 und 43.
Hinweis - In diesem Fall der Zerlegung haben wir es vermieden, die
gemeinsamen Teilbarkeit durch 2, 3, 5, 11 zu untersuchen, und wir haben es
vermieden, auf der Suche nach dem Primfaktor durch Versuch und Irrtum
(kontraproduktive Anwendungsarbeit) vorzugehen, wodurch wir 9 vollständige
Teilungen erspart haben was notwendig gewesen wäre, bevor wir wussten, dass
1763 durch 41 teilbar ist;. Tatsächlich hätten wir 1763 zuerst durch 7, dann
durch 13, 17, 19, 23, 29, 31, 37, 41 teilen müssen, nur um in dieser letzten
Division den Rest 0 zu erhalten, der für die Identifizierung der
Primfaktoren erforderlich ist.
5 - Lassen Sie eine gerade Zahl aufteilen:
Teilen Sie durch 2, bis Sie eine ungerade Zahl finden, die dann mit dem
Lineal aufgeschlüsselt wird.
Der
Pfeil zeigt auf 1500. Die oberste Hilfslinie berührt 67. Daher
ist die zu zerlegende Zahl 1567. In der Mitte des Winkelmessers sehen
wir einen schwarzen Punkt. Bedeutung: 1567 ist eine Primzahl.
Der
Pfeil zeigt auf 700. Die oberste Hilfslinie berührt 41. Die zu
zerlegende Zahl ist 741. In der Mitte des Winkelmessers sehen wir
drei Durchmesser, die 3, 13 und 19 berühren. Bedeutung: 741 ist teilbar
durch 3, durch 13 und 19. WICHTIGER HINWEIS Die Teilbarkeitskarte ist
durch reguläre Patente in Italien und in der Welt geschützt. Fälscher und
Händler, die diese gültigen Patente missachten, werden nach dem Gesetz
bestraft (Art. 88 RD 29. Juni 1939).
Rechenwerkzeug.de