Das Staffelwalzenprinzip
Quelle: Archiv E. Anthes
Einmal einstellen, mehrmals addieren: Die Staffelwalze
| Von einer Maschine erwartet man im Allgemeinen einen automatischen Mechanismus, der eine bestimmte Denkarbeit ersetzt. Insofern sind Abakus und Rechenbrett eigentlich keine Maschinen, sondern nur Merkhilfen, die das teure Papier ersetzen. Die ersten automatischen mechanischen Vorrichtungen finden sich bei der Schickard'schen Maschine von 1624 und der Pascal'schen Maschine von 1642 im automatischen Zehnerübertrag. | |
|
|
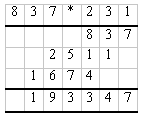
Wollte der Benutzer multiplizieren, beispielsweise 837 * 231 so musste er die drei Teilprodukte 837 * 2, 837 * 3 und 837 * 1 im Kopf ausrechnen und jeweils um eine Stelle verschoben addieren. Pascals Maschine half nur bei der Addition der Teilprodukte. Schickards Maschine unterstützte dagegen auch die Multiplikation insofern als man bei ihr die Teilprodukte nicht im Kopf berechnen musste, sondern von Napier-Skalen ablesen konnte. |
|
|
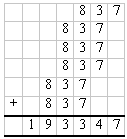
Der Benutzer konnte auch anders vorgehen: Er konnte die Zahl 837 einmal von der Einerstelle aufwärts eingeben, dann dreimal von der Zehnerstelle aufwärts und dann noch zweimal von der Hunderterstelle aufwärts. So wurde aus einer Multiplikation eine Addition. Die Krux bei der Sache war nur: Jeder dieser Summanden musste individuell in das Zählwerk eingedreht werden, was nicht nur zeitaufwendig, sondern mindestens ebenso fehlerträchtig war wie die Multiplikation im Kopf. Maschinell war dieses Prinzip aber leichter umzusetzen als das erste. |
|
|
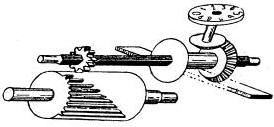
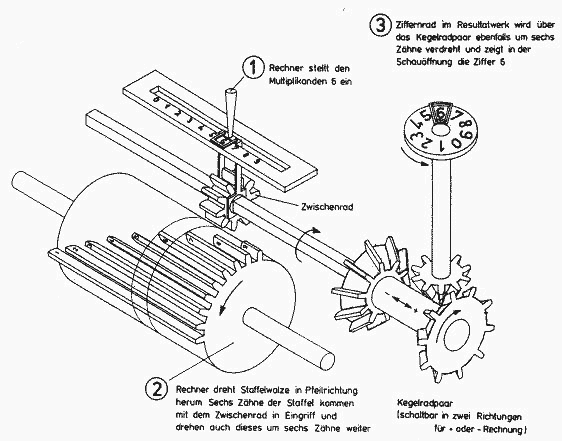
Gefragt war dabei ein Mechanismus, der es erlaubte, die erste Zahl (837) nur einmal einzustellen und dann beliebig oft in ein Zählwerk "einzudrehen". Der erste, dem es gelang, einen solchen Mechanismus zu bauen, war der deutsche Mathematiker Gottfried Wilhelm Leibniz: Er erfand die Staffelwalze, ein Zahnrad mit unterschiedlich langen Zähnen. Diese Walze wird beim Rechnen gedreht und treibt ein kleines Zahnrad an. Je nachdem, wo das kleine Zahnrad die Staffelwalze abgreift, dreht es sich bei einer Umdrehung der Staffelwalze um null bis neun Positionen weiter. Leibniz spendierte jeder Stelle eine eigen Staffelwalze und trieb alle durch eine gemeinsame Kurbel an. |
|
|
Wenn der Benutzer nun im Einstellwerk die 837 eingab, konnte er mit einer Umdrehung der Kurbel die ganze Zahl ins Resultatzählwerk einspeisen. Durch mehrmaliges Drehen der Kurbel wurde die gleiche Zahl ohne erneutes Einstellen nochmals addiert. Da das Resultatwerk außerdem gegenüber dem Einstellwerk verschoben werden konnte, war die Beispielrechnung jetzt durch eine Einstellung, sechs Kurbeldrehungen und zwei Stellenverschiebungen zu erledigen. |
|
Allerdings klingt das einfacher, als es ist. Die Rädchen des Resultatwerks wurden ja nicht nur von den Staffelwalzen gedreht, auch untereinander musste der Zehnerübertrag funktionieren. Dieses Problem bedingte einen so komplizierten Aufbau und erforderte eine so große Präzision der Teile, dass die Maschine zu Leibnitz' Lebzeiten das Prototypstadium nicht verließ. In Serie gebaut und verkauft wurden Staffelwalzenmaschinen erst über 100 Jahre nach Leibniz' Tod von dem französischen Mechaniker Xavier Thomas aus Colmar. Hier eine späte Thomas Maschine:
|
|
|
Und so sahen Thomas-Maschinen von innen aus (hier eine Bunzel Arithmometer): |
|
Rechenwerkzeug.de