Logomat Pfiffikus 2001

Der Pfiffikus war das kleinste und erfolgreichste einer Reihe einfacher Rechengeräte, die die hessische Firma Logomat um 1970 auf den Markt brachte. Dabei handelte es sich meist um logarithmische Rechenscheiben, die auf einen bestimmten Einsatzzweck hin konstruiert waren - etwa Benzinverbrauch oder Währungsumrechnungen. Häufig wurden sie als Werbegeschenk im Zusammenhang mit einem bestimmten Produkt verteilt, sie waren daneben in der Regel aber auch allgemein einsetzbar. Viele davon besaßen eine Spiralskala mit zwei oder drei Windungen.  Ob sie von irgend jemand noch wirklich ernsthaft zum Rechnen benutzt wurde, ist heute nicht mehr festzustellen. Dass das Konzept ernst genommen werden wollte, zeigt die gleichzeitig hergestellte Profi-Variante mit austauschbaren Einstellscheiben.

 

Unter den Rechenscheiben stellt der Pfiffikus eine Klasse für sich dar. Bei nur 4,8 cm Außendurchmesser (die Hülle mit Anleitung hat Streichholzbriefchengröße) besitzt er immerhin eine 35 cm lange Skala, d.h. die Ablesegenauigkeit ist besser als bei einem Standard-Rechenstab mit 25 cm-Skala. Man erkauft sich diesen Vorteil durch die zunächst ungewohnte Bedienung (in Deutschland waren fast ausschließlich Zwei-Skalen-Rechenstäbe und -scheiben im Einsatz) und durch die neben dem Überschlag zusätzliche Überlegung, auf welcher Skala man das Ergebnis ablesen muss. Dies ist bei drei Spiralwindungen überschaubar. Beim Vorbild, der sehr viel größeren amerikanischen Atlas, die nach dem gleichen Prinzip, aber mit etwa 30 Spiralwindungen arbeitete, erhält man zwar eine größere Genauigkeit, muss aber zunächst wie bei den Fowler-Rechenuhren eine Grobkalkulation vornehmen, um die richtige Spiralwinung zum ABlesen zu bestimmen. Ihren Testrechner bekommen Sie hier.

LOGOMAT - das Rechenwunder in Kleinformat

Den pfiffiKUS braucht, wer schneller rechnen will.

Sie müssen nur eines erfasst haben:

das Geheimnis des Einstell-Winkels.

 

 

Mit dem Einstellwinkel zwischen dem roten und dem schwarzen Zeiger legen Sie das Verhältnis zwischen den Ausgangszahlen fest. Sie rechnen dann, indem Sie die Zahlenskala unter diesem Einstellwinkel verschieben.

Probieren Sie an Beispielen aus, wie einfach und schnell Sie mit dem Einstellwinkel auf dem pfiffikus® rechnen.

 

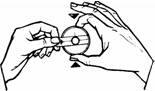
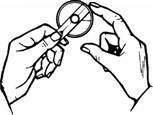
Drei technische Hinweise:

1.          Zum Einstellen des roten Zeigers drehen Sie die Zahlenskala unter den beiden Zeigern. Dann nehmen Sie die Scheibe des pfiffiKUS"' fest zwischen Daumen und Zeigefinger der einen Hand, so dass die Scheibe mit dem roten Zeiger sich nicht mehr drehen kann, und stellen den schwarzen Zeiger ein (Abb. 1). Dann fassen Sie den pfiffiKUS9 fest am schwarzen Zeiger und drehen an der Metallscheibe. Der Einstellwinkel zwischen dem roten und dem schwarzen Zeiger verändert sich nicht, aber die Zahlenskala darunter dreht sich (Abb. 2).

Abbildung 1

Abbildung 2

 

2.      Sie haben bestimmt sofort gesehen, dass die Zahlen 1 bis 10,0 auf einer Skala in Form einer Spirale angeordnet sind. Die Zahlen 1, 2, 3, 4 usw. stehen dabei für alle Werte mit der gleichen ersten Stelle, also auch für 10, 20, 30, 40 usw. Die Zahlen 1,1; 1,2; 1,3; 1,4 usw. stehen folglich auch für 11, 12, 13, 14 usw. Es ist also gleich, ob Sie mit kleinen oder mit großen Zahlen rechnen müssen. Den pfiffiKUS können Sie immer gebrauchen.

 

3.    Die Zahlenspirale hat insgesamt drei Windungen. Sie finden den für das Ergebnis jeweils richtigen Spiralgang so:

Beim Einstellen des Winkels achten Sie darauf, um wie viel Spiralgänge sich die mit dem roten Zeiger und dem schwarzen Zeiger eingestellten Zahlen unterscheiden. Um genauso viele Spiralgänge unterscheidet sich das Ergebnis von der nach dem Drehen der Scheibe eingestellten Zahl. Sonderfall: Wenn das Ergebnis unter 1 oder über 10,0 liegt, wird das andere Ende der Spirale als Fortsetzung angesehen (Abb. 3 bis 6).

Abbildung 3 und 4:

Die Einstellungszahlen liegen auf dem gleichen Spiralgang,
deshalb gilt das auch für alle anderen Einstellungen.

 

Abbildung 5 und 6:

Die Einstellungszahlen liegen auf zwei aufeinander folgenden Spiralgängen.
Deshalb gilt das auch für alle Einstellungen.

Frage: Was kostet... ?

Beispiel 1:

1 Buch kostet 12,50 DM.
Was kosten 7 Bücher?

Einstellen des Winkels:
Roter Zeiger auf 1 (= Bücher)
Schwarzer Zeiger auf 12,5 (= DM)

Rechnen (= Scheibe drehen):
Roter Zeiger (= Bücher) auf 7.
Ablesen beim schwarzen Zeiger = 87,5.

Ergebnis:
7 Bücher kosten 87,50 DM.

 

Beispiel 2:

1 Liter Benzin kostet 57,5 Pf.
Was kosten 22,5 Liter?

Einstellen des Winkels:

Roter Zeiger auf 1 (= Liter)
Schwarzer Zeiger auf 57,5 (= 0,575 DM)
Achtung: 57,5 liegt zwei Spiralgänge über 1 und einen Spiralgang unter 10. Das Ergebnis muss also auch zwei Spiralgänge über oder einen Spiralgang unter der Einstellzahl liegen.

Rechnen (= Scheibe drehen):
Roter Zeiger (= Liter) auf 22,5.
Ablesen einen Spiralgang darunter beim schwarzen Zeiger bei 12,94.

Ergebnis:
22,5 Liter Benzin kosten 12,94 DM

Frage: Was kann man mit ... DM machen?

Beispiel: Wieviel Liter Benzin (á 57,5 Pf.) erhält man für 25 DM?

Einstellen des Winkels:
Roter Zeiger auf 1 (=Liter).
Schwarzer Zeiger auf 57,5 (=0,575 DM)
Achtung: 10 liegt einen Spiralgang über 57,5!

Rechen (=Scheibe drehen):
Schwarzer Zeiger (DM) auf 25
Ablesen einen Spiralgang darüber beim roten Zeiger (=Liter) bei 43,5.

Ergebnis: Für 25 DM erhält man 43,5 Liter Benzin

Frage: Durchschnittlicher Verbrauch

Beispiel: Bei 412 km wurden 35,5 Liter Benzin verbraucht, wieviel pro 100 km?

Einstellen des Winkels:
Roter Zeiger auf 41,2 (= 412 km).
Schwarzer Zeiger auf 35,5 (= Liter)

Rechen (= Scheibe drehen):
Roter Zeiger auf 10 (= 100 km)
Ablesen beim schwarzen Zeiger = 8,6

Ergebnis: Der durchschnittliche Kraftstoffverbrauch pro 100 km betrug 8,6 Liter.

Frage: Prozentrechnen
und Zinsrechnen

Beispiel 1
7,5 % von 346.- DM = ?

Einstellen des Winkels:
Roter Zeiger auf 10 (= 100- DM).
Schwarzer Zeiger auf 7,5 (= Betrag bei 100.- DM).

Rechnen (= Scheibe drehen):
Roter Zeiger auf 346.
Ablesen beim schwarzen Zeiger = 26.

Ergebnis:
7,5 % von 346.- DM sind 26.- DM. (2,6 oder 260 nicht möglich, da Ergebnis mehr als 10 und weniger als 100 sein muss.)

Frage: Einkaufspreis, Verkaufspreis, Aufschlag, Rabatt?

Beispiel 1:
Einkaufspreis = 7,- DM, Verkaufspreis = 8,80 DM. Wie viel Aufschlag?

Einstellen des Winkels:
Roter Zeiger auf 7 (= Einkaufspreis),
Schwarzer Zeiger auf 8,8 (= Verkaufspreis).

Rechnen (= Scheibe drehen):
Roter Zeiger auf 1 (= 100 %).
Ablesen beim schwarzen Zeiger bei 1,26.

Ergebnis:
Der Verkaufspreis von 8,80 DM sind 126 % vom Einkaufspreis, der Aufschlag beträgt also 26 %.

 

Beispiel 2:
Wie groß ist der Aufschlag beim Einkaufspreis von 2,20 DM und einem Verkaufspreis von 5,40 DM?

Einstellen des Winkels:
Roter Zeiger auf 2,2 (= Einkaufspreis).
Schwarzer Zeiger auf 5,4 (= Verkaufspreis).
Achtung: 5,4 liegt einen Spiralgang über 2,2.

Rechnen (= Scheibe drehen):
Roter Zeiger auf 1 (= 100 %).
Ablesen beim schwarzen Zeiger einen Spiralgang darüber bei 245.

Ergebnis:
5,40 DM sind zu 2,20 DM 245 %, der Aufschlag beträgt also 145 %.

 

Beispiel 3:
Wie groß ist der Rabatt, wenn der Verkaufspreis 8,80 DM und der Einkaufspreis 7,- DM beträgt?

Einstellen des Winkels:
Roter Zeiger auf 7 (= Einkaufspreis).
Schwarzer Zeiger auf 8,8 (= Verkaufspreis).

Rechnen (= Scheibe drehen):
Schwarzer Zeiger auf 10 (= 100 %).
Ablesen beim roten Zeiger = 79,5.

Ergebnis:
Der Einkaufspreis ist 79,5 % vom Verkaufs­preis, der Rabatt beträgt mithin 20,5 % (100%-79,5% = 20,5%).

 

Beispiel 4:

Wie viel beträgt der Verkaufspreis, wenn auf 25,40 DM 46 % aufgeschlagen werden sollen?

Einstellen des Winkels:
Roter Zeiger auf 1 (= 100 %).
Schwarzer Zeiger auf 25,4 (= DM).
Achtung: 25,4 liegt einen Spiralgang über 1!

Rechnen (= Scheibe drehen):
Roter Zeiger auf 146 (= 100 % + 46 %).
Ablesen einen Spiralgang darüber beim schwarzen Zeiger bei 37,08.

Ergebnis:
Bei 46 % Aufschlag und einem Einkaufspreis von 25,40 DM beträgt der Verkaufspreis 37,08 DM.

 

Beispiel 5:

Wie hoch ist der Einkaufspreis, wenn auf 25,40 DM 46 % Rabatt gewährt werden?

Einstellen des Winkels:
Roter Zeiger auf 1 (= 100%).

Schwarzer Zeiger auf 25,4 (= DM).
Achtung: 25,4 liegt einen Spiralgang über 1!

Rechnen (= Scheibe drehen):
Roter Zeiger auf 54 (= 100 % - 46 %).
Ablesen einen Spiralgang darüber, da nicht möglich im unteren Spiralgang beim schwarzen Zeiger = 13,72.

Ergebnis:
Der Einkaufspreis beträgt 13,72 DM, wenn auf 25,40 DM 46 % Rabatt gewährt werden.

Frage: Mehrwertsteuerberechnung

Beispiel 1:
Mehrwertsteuer von 31.- DM?

Einstellen des Winkels:
Roter Zeiger auf 10 (= 100.- DM).
Schwarzer Zeiger auf 11 (= Mehrwertsteuer bei 100.- DM).

Rechnen (= Scheibe drehen):
Roter Zeiger auf 31.
Ablesen beim schwarzen Zeiger = 3,41.

Ergebnis:
Die Mehrwertsteuer von 31.- DM beträgt 3,41 DM. (34,1 DM oder 0,34 DM nicht möglich, da der Betrag weniger als 10,- DM und mehr als 1,- DM sein muss.)

 

Beispiel 2:
Nettopreis + Mehrwertsteuer? Nettobetrag 31.- DM, Verkaufspreis?

Einstellen des Winkels:
Roter Zeiger auf 1 (= 100%).
Schwarzer Zeiger auf 11,1 (= 111%).

Rechnen (Scheibe drehen):
Roter Zeiger auf 31.
Ablesen beim schwarzen Zeiger = 34,4.

Ergebnis:
Der Verkaufspreis einschließlich Mehrwertsteuer beträgt 34,41 DM bei einem Nettopreis von 31,- DM. (2. Stelle nach dem Komma schätzen.)

Frage: Währungsumrechnung

(Jeder Zeiger bedeutet immer eine Währung)

Beispiel 1:
Wie viel DM sind 15 $. wenn 1 $ = 3,66 DM sind?

Einstellen des Winkels:
Roter Zeiger auf 1 (= Dollar).
Schwarzer Zeiger auf 3,66 (= DM). Achtung: 3,66 = zwei Spiralgänge über 1.

Rechnen (= Scheibe drehen):
Roter Zeiger auf 15 (= $).
Ablesen zwei Spiralgänge darüber beim schwarzen Zeiger 54,9.

Ergebnis:
15 $ sind 54,90 DM.

 

Beispiel 2:
Wie viel $ sind 27,40 DM, wenn 1 $ 3,66 DM sind?

Einstellen des Winkels:
Wie Beispiel 1

Rechnen (= Scheibe drehen):
Schwarzer Zeiger auf 27,4 (= DM).
Ablesen beim roten Zeiger (= $) zwei Spiralgänge darunter, da nicht möglich im obersten Spiralgang bei 7,49.

Ergebnis:
27,40 DM sind 7,49 $.

Frage: Multiplizieren (Malnehmen)

18 X 8 = ?

Hinweis: Frage zerlegen in: 1 X  = 8,  18 x = ?

Einstellen des Winkels:
Roter Zeiger auf 1,
schwarzer Zeiger auf 8.
Ablesen (= Scheibe drehen):
Roter Zeiger auf 18. Ablesen bei 144.

Ergebnis:
18 X 8 = 144.

Frage: Dividieren (Teilen)

216 : 9 = ?

Hinweis: Frage zerlegen in: 216 :9 = ? :1

Einstellen des Winkels:
Roter Zeiger auf 216.
Schwarzer Zeiger auf 9.
Achtung: Einstellung roter Zeiger zwei Spiralgänge unter Einstellung schwarzer Zeiger!

Rechnen (= Scheibe drehen):
Schwarzer Zeiger auf 10.
Ablesen zwei Spiralgänge tiefer beim roten Zeiger bei 24.

Ergebnis:
216 : 9 = 24.

Frage: Vergrößern und Verkleinern

Beispiel: Eine Seite von 45 cm soll im Verhältnis 3 : 4 vergrößert werden.

Einstellen des Winkels:
Roter Zeiger auf 3. Schwarzer Zeiger auf 4.

Rechnen (= Scheibe drehen):
Roter Zeiger auf 45.
Ablesen beim schwarzen Zeiger bei 60.

Ergebnis:
Die Seite wird 60 cm lang.

Der Logomat pfiffiKUS wurde ausgezeichnet!

Auf der PSI-Tagung 1971 in Düsseldorf wurde der LOGOMAT-Pfiffikus zum interessantesten Werbegeschenk der Gruppe 1 (Verkaufsförderungs-Artikel) gewählt.

Logomat liefert außerdem:

mini 2000, ein programmierbarer Kassettenrechner in Westentaschenformat.
Währungsspiralen für die Umrechnung von verschiedenen Währungen zum Tageskurs.
Mehrwertsteuerspirale, auf einen Blick Bruttobetrag, Nettobetrag und Mehrwertsteuer.
Zinsspirale, berechnet die Zinsen auf den Tag genau.
Sonderanfertigungen von Rechenschiebern und Rechenscheiben.

Die vorstehende Anleitung bezieht sich auf das einseitige Modell. Der doppelseitige Pfiffikus besitzt zwei zusätzliche Skalen auf der Rückseite: Stellt man auf der Vorderseite eine Zahl unter den Läufer (2), so kann man auf der Rückseite die zugehörige zweite Potenz (4) und dritte Potenz (8) ablesen. Kehrt man das Verfahren um, so lassen sich Quadrat- und Kubikwurzeln bestimmen. Quadratwurzeln finden sich auf der gleichen Spitalwindung, bei Kubikwurzeln ist eine Überschlagsrechnung notwendig. Während auf der Vorderseite die Skala auf das Aluminium und die beiden Markierungen auf Plexiglas-Overlays aufgedruckt sind, ist es auf der Rückseite umgekehrt. Dort befindet sich die Skala auf dem Overlay, und die Aluminiumscheibe trägt einen schwarzen Zeiger.

Der einseitige Logomat Pfiffikus besteht aus fünf Teilen, der doppelseitige aus sechs: einer Aluscheibe mit aufgedruckter Skala, einer transparenten Scheibe mit rotem Zeiger und einem Läufer mit schwarzem Zeiger. Diese Teile werden durch eine Art roten Druckknopf zusammengehalten. Die beiden Zeiger sitzen straff aufeinander, so dass sie sich nicht verstellen, während die Aluscheibe unter ihnen verdreht wird. Der doppelseitige Pfiffikus besitzt eine zusätzliche Skalenscheibe aus Plexiglas auf der Rückseite, die mit dem Läufer der Vorderseite fest verbunden ist. Hier die Ergänzungen in der Bedienungsanleitung zur doppelseitigen Ausgabe. Ursprünglich gab es eine weitere Skala von 0 bis 10 auf der Aluscheibe, sodass man auch nach dem Skala-Skala-Verfahren multiplizieren konnte. In der abgebildeten Ausführung ist diese Skala entfallen.

Die Rückseite des pfiffiKUS*
ermöglicht Ihnen, einige weitere, in der Praxis häufig benötigte Rechenoperationen in Sekundenschnelle durchzuführen.

Hier die Hinweise zum Einstellen:


 

Potenzieren
Zum Quadrieren (X³) die Zahl (X) mit dem schwarzen Zeiger auf der Vorderseite einstellen und auf der Rückseite im gleichen Spiralgang über dem schwarzen Zeiger der Metallscheibe ablesen.
Beispiel:
Die Seiten eines Quadrates sind 4 cm lang.
Wie groß ist die Fläche des Quadrates?
Einstellen:
Auf der Vorderseite schwarzen Zeiger auf 4.
Achtung: 4 liegt im zweiten Spiralgang.
Ablesen:
Auf der Rückseite im zweiten Spiralgang über dem schwarzen Zeiger: 16.
Ergebnis: Die Fläche des Quadrates beträgt 16 cm².


Zum Kubieren (X³) die Zahl (X) mit dem schwarzen Zeiger auf der Vorderseite einstellen und auf der äußeren Skala der Rückseite (X³) über dem schwarzen Zeiger der Metallscheibe ablesen.
Beispiel:
Die Seiten eines Würfels sind 4 cm.
Wie groß ist sein Rauminhalt?
Einstellen:
Schwarzer Zeiger der Vorderseite auf 4.
Ablesen:
Auf der Rückseite über dem schwarzen Zeiger der äußeren Skala: 64.
Ergebnis:
Der Rauminhalt des Würfels beträgt 64 cm³.
 

Radizieren (Wurzelziehen)
Zum Berechnen von 2√X auf der Rückseite die Zahl (X) über dem schwarzen Zeiger der Metallscheibe einstellen und auf der Vorderseite im gleichen Spiralgang 2√X ablesen.
Beispiel: Eine quadratische Fläche ist 315 m2 groß.
Wie lang sind die Seiten?
Einstellen:
Schwarzer Zeiger der Rückseite unter 3,15.
Ablesen:
Auf der Vorderseite im gleichen Spiralgang unter 1,77.
Ergebnis:
Die Seiten des Quadrates sind 17,7 m lang.

Zum Berechnen der 3√X auf der Rückseite die Zahl (X) auf der äußeren Skala der durchsichtigen Scheibe einstellen und auf der Vorderseite im ersten Spiralgang unter dem schwarzen Zeiger ablesen.
 


Besonderer Hinweis:
Im ersten Spiralgang ist dann 3VX angezeigt, im zweiten Spiralgang √ioX,  im dritten Spiralgang 3√100X.
 

Beispiel: X = 2    3√2=?
Einstellen:
Auf der Rückseite die 2 der äußersten durchsichtigen Skala über den schwarzen Zeiger der Metallscheibe.
Ablesen:
Auf der Vorderseite unter dem schwarzen Zeiger.
Ergebnis:
3√2 = 1,26
3√20 = 2,714
3√2oo = 5,85

Rechenwerkzeug.de