Wozu braucht man Rechenmaschinen?

In der „Zeitschrift für Vermessungswesen“ erschien in Heft 10/1897 ein Artikel des Herausgebers Dr. W. Jordan über die Leibniz’sche Rechenmaschine. Jordan zitiert darin wörtlich eine in der königlichen Bibliothek zu Hannover befindliche in Latein verfasste Abhandlung von Leibniz über die Anfertigung seiner Rechenmaschine und liefert eine deutsche Übersetzung nach.
Ein Faksimilie des Textes findet sich unter https://archive.org/details/zeitschriftfrve10vermgoog/page/n303 An späterer Stelle ides gleichen Jahresbandes, in Heft 18/1897 findet sich ein Bericht des Rechenmaschinenfabrikanten Artur Burkhardt über seine Restaurierung der einzigen erhaltenen Leibniz-Maschine. https://archive.org/details/zeitschriftfrve10vermgoog/page/n409 .

Ausgehend von seiner Kenntnis der Pascaline entwickelt Leibniz in diesem Text seine Vorstellungen davon, wie man diese Maschine zur Ausführung aller vier Grundrechenarten erweitern müste und welche Vorteile er sich als Wissenschaftler von der Mechanisierung der Rechenvorgänge erhoffte.

Machina arithmetica in qua non additio tantum et subtraction sed et multiplicatio nulle, et divisio vero paene nullo animi labore peragantur

Rechenmaschine, in der nicht nur die Addition und Subtraktion, sondern auch die Multiplikation ohne und die Division fast ohne alle geistige Arbeit ausgeführt wird.

Gottfried Wilhelm Leibniz (Übersetzung Richard Jordan)

Als ich vor einigen Jahren zum ersten Male ein Instrument sah, mit Hilfe dessen man seine eigenen Schritte ohne zu denken zählen kann, kam mir sogleich der Gedanke, es ließe sich die ganze Arithmetik durch eine ähnliche Art von Werkzeug fördern, indem nicht nur die bloße Zählung, sondern auch die Addition mit der Subtraktion und die Multiplikation mit der Division mit sicherem Erfolge von der entsprechend eingerichteten Maschine selbst leicht und bequem ausgeführt würde.

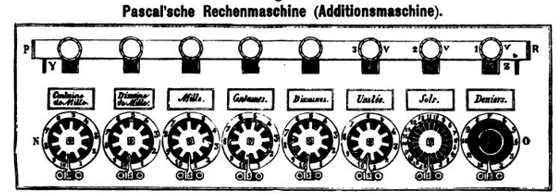
(Abbildung aus dem Artikel von Jordan)

Original-Pascaline im Mathematisch-physikalischen Salon Dresden (eigene Aufnahme)

Noch war mir damals das Pascal‘sche Rechenkästchen nicht bekannt geworden; ich glaube, es war nicht hinlänglich in die Öffentlichkeit gedrungen. Aber sobald ich in der Vorrede seiner „nachgelassenen Gedanken'' (sein „arithmetisches Dreieck" sah ich erst in Paris) nur den Namen einer Rechenmaschine bemerkte, fragte ich sogleich brieflich einen Freund in Paris, wie es damit stände. Als ich von diesem erfahr, dass eine derartige Maschine dort (?) vorhanden sei, bat ich den hochwürdigen Carcavius in einem Brief um eine Aufklärung über die Arbeit, die sie leiste. Er antwortete, die Addition und Subtraktion würden ohne Weiteres, das Übrige nur auf Umwegen in ihr ausgeführt, indem Addition und Subtraktion wiederholt würden und noch eine andere Rechnung hinzukäme. Ich schrieb zurück, ich wage noch etwas Weiteres in Aussicht zu stellen, dass nämlich auch die Multiplikation ebenso wie die Addition in der Maschine mit größter Schnelligkeit und Sicherheit bewerkstelligt würde. Jener erwiderte, dies würde nicht unerwünscht sein, und machte mir zugleich Mut, mein Vorhaben an diesem Orte bei der hochansehnlichen Königlichen Akademie auseinanderzusetzen.

Vor allem muss man wissen, dass die Maschine aus zwei Hauptteilen besteht, von denen der eine für die Addition oder Subtraktion), der andere für die Multiplikation oder Division bestimmt ist, und dass der eine sich dem andern anpassen muss.

Die Additions- und Subtraktions-Maschine stimmt mit dem Pascal‘schen Rechenkästchen im Großen und Ganzen überein. Aber es muss noch etwas hinzukommen wegen der Hinzufügung der Multiplikation, dass nämlich mehrere, ja sogar alle Additionsräder zur selben Zeit umgedreht werden können, indem keines das andere stört und trotzdem ein beliebiges vorangehen kann, das wenn es sich einmal ganz herumgedreht hat, die Einheit auf das nächstfolgende überträgt. Wenn dies in dem Pascal‘schen Rechenkästchen nicht geleistet worden ist, so wird es demselben unschwer hinzugefügt werden können.

Die Multiplikationsmaschine wird aus zwei Reihen von Rädern bestehen: teils aus gleich großen, teils aus ungleichen. Die ganze Maschine wird also drei Arten von Rädern haben: 1) die Additionsräder, 2) die Räder des Multiplikanden, 3) die Räder des Multiplikators oder multiplizierenden Räder.

Die Additions- oder dekadischen Räder sind die, welche jetzt schon in dem Additionskästchen Pascals zu sehen sind, und in der beigefügten Figur mit den Zahlen 1, 10, 100 usw. bezeichnet sind. Von diesen ist jedes mit 10 Zähnen, und zwar unbeweglichen, versehen.

Die Räder, die den Multiplikanden darstellen, sind sowohl unter sich, als auch mit den Additionsrädern gleich groß und ebenfalls jedes mit 10 Zähnen versehen, aber diese sind beweglich, so dass bald 5, bald 6 Zähne hervorstehen usw., je nachdem nämlich die zu multiplizierende Zahl auf ihnen 5oder 6-fach darzustellen ist. Von diesen Rädern müssen so viele vorhanden sein, wie der Multiplikand Ziffern besitzen kann, besteht z. B. der Multiplikand 365 besteht aus den 3 Ziffern, 3, 6 und 5 so sind in diesem Falle ebenso viele Räder anzuwenden, nämlich 3.

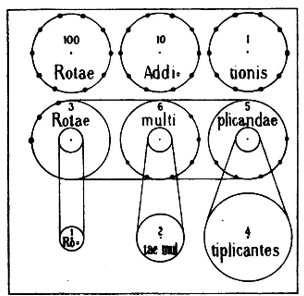
Nachzeichnung eines frühen Entwurfs von Leibniz für eine Vierspeziesmaschine. (Abbildung aus dem Artikel von Jordan)

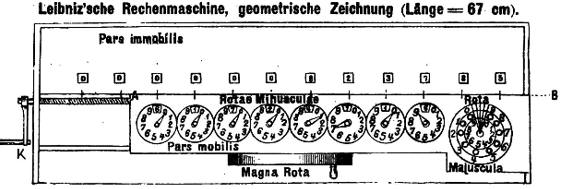
Die erhaltene Maschine, das letzte von mindestens vier Modellen (Abbildung aus dem Artikel von Jordan)
Das letzte erhaltene Original steht heute in der Gottfried Wilhem Leibniz Bibliothek in Hannover

Nachbau der Leibniz-Maschine durch Nikolaus Joachim Lehmann 1990. Technische Sammlungen, Dresden (eigene Aufnahme)

Nachbau durch die Firma Brunsviga 1924.  Deutsches Museum München (Abbildung im Museumskatalog)

Auf diesen Rädern ist die zu multiplizierende Zahl einzustellen, wenn bewirkt werden soll, dass aus dem rechten Rade 5 Zähne hervorragen, aus dem mittleren 6, aus dem linken 3. Damit dieses schnell und leicht geschehen kann, bedarf es einer ganz besonderen Einrichtung, deren Auseinandersetzung mich hier zu weit führen würde.

Es sollen nun die Räder des Multiplikanden den Additionsrädern so angefügt werden, dass das letzte dem letzten, das vorletzte dem vorletzten, das vorvorletzte dem vorvorletzten entspricht, oder 5 und 1, 6 und 10, 3 und 100 sich entsprechen. In dem Additionskästchen selbst aber soll durch kleine Öffnungen die aufgesetzte Zahl 0, 0, 0 usw. sichtbar sein, oder auch nur Null. Wenn man nun nach dieser Anfügung annimmt, dass 365 mit der Einheit 1 multipliziert wird, so müssen die Räder 3, 6 und 5 einmal umgedreht werden (mit der Umdrehung eines einzigen aber drehen sich sämtliche, weil sie gleich und durch Sehnen verbunden sind, was in Folgendem noch deutlicher werden wird) und die Zähne derselben, welche jetzt hervorragen, werden ebenso viele unbewegliche Zähne an den Rädern 100, 10 und 1 umdrehen, und so wird daher die Zahl 365 auf das Additionskästchen übertragen.

Aber gesetzt, es sei die Zahl 365 mit einem beliebigen Multiplikator (124) zu multiplizieren, so bedarf es jetzt der dritten Art von Rädern, der multiplizierenden Räder oder der Räder des Multiplikators. Die Zahl dieser Räder möge 9 sein, und während die Räder des Multiplikanden veränderlich sind, so dass dasselbe Rad zu verschiedener Zeit bald die Einheit 1, bald 9 darstellen kann, so bezeichnen dagegen die Räder des Multiplikators eine bestimmte Ziffer, teils 9, teils 1 usw.

Die Sache gebt nun so zu: Jedes beliebige Rad des Multiplikators ist mit einer kleinen Winde, die auf dem entsprechenden Rad des Multiplikanden befestigt ist, durch eine Sehne oder Kette verbunden. Daher wird das Rad des Multiplikators ebenso viele Einheiten darstellen, als sein Durchmesser denjenigen der entsprechenden Winde in sich enthält. Denn so oft dreht es die Winde um, während es sich selbst nur einmal umdreht. Wenn daher der Durchmesser des Rades viermal den Durchmesser der Winde enthält, so wird das Rad die Zahl 4 darstellen.

Bei einer einmaligen Umdrehung des multiplizierenden Rades, dessen entsprechende Winde den 4. Teil seines Durchmessers hat, wird sich inzwischen die Winde viermal um sich selbst drehen, und mit ihr auch das Rad des Multiplikanden, auf welchem die Winde befestigt ist. Wenn aber das Rad des Multiplikanden sich viermal umdreht, werden auch seine Zähne viermal an dem betreffenden Additionsrad ihren Lauf machen, und daher wird die Zahl seiner Einheiten so oft (nämlich viermal) in dem Additionskästchen wiederholt werden.

Durch ein Beispiel wird die Sache am deutlichsten werden: 365 sei mit 124 zu multiplizieren.

Zuerst muss die ganze Zahl 365 mit 4 multipliziert werden. Man drehe daher mit der Hand einmal das multiplizierende Rad 4, dann wird sich zugleich die entsprechende Winde viermal umdrehen (da ja ihr Durchmesser um so viel kleiner ist, und mit ihr wird sich auch das Rad des Multiplikanden 5, auf dem diese Winde befestigt ist, viermal um sich selbst drehen. Und da das Rad 5 auch 5 hervorstehende Zähne hat, so wird es bei jeder Umdrehung auch die Zähne des entsprechenden Additionsrades 1 um 5 fortbewegen und so in dem Additionskästchen viermal 5 oder 20 Einheiten bilden.

Das Rad 6 des Multiplikanden ist mit dem Rade 5 des Multiplikanden durch eine andere Sehne oder Kette verbunden, und das Rad 3 des Multiplikanden ebenfalls mit dem Rade 6. Da sie nun gleich sind, muss, während das Rad 5 sich viermal umdreht, zugleich auch das Rad 6 bei viermaliger Umdrehung 24 Zehner ergeben (denn es greift in das dekadische Additionsrad 10 ein), und das Rad 3, das in das Additionsrad 100 eingreift, muss 12 Hunderte bilden; es ergibt sich also als Summe 1460.

Auf diese Weise ist 365 mit 4 multipliziert, was die erste Operation ist. Damit es nun auch mit 2 (oder vielmehr 20) multipliziert wird, muss die ganze Multiplikationsmaschine um einen Schritt vorgerückt werden, sodass nun das Rad 5 des Multiplikanden und das Rad 4 des Multiplikators ihre Stelle unter dem Additionsrad 10 erhalten, während sie vorher sich unter Rad 1 befanden, und ebenso 6 und 2 unter 100 und 4 und 1 unter 1000. Nach dieser Anordnung drehe man einmal das Rad 2 des Multiplikators ; dann müssen sich auch zugleich die Räder 6 und 3 zweimal umdrehen, und 5, das nun zweimal in das Additionsrad 10 eingreift, wird 10 Zehner, 6, das in 100 eingreift, 12 Hunderter, 3 das in 1000 eingreift, 6 Tausende ergeben; es kommen also im Ganzen 7300 heraus. Dies wird dann zu dem Ergebnis der vorigen Umdrehung, 1460, hinzuaddiert.

Damit nun auch als 3. Operation mit 1 (oder vielmehr 100) multipliziert wird, rücke man von neuem die Multiplikationsmaschine vor natürlich zugleich die Räder des Multiplikanden und Multiplikators, während die Additionsräder an ihrer Stelle bleiben) und es mögen Rad 5 und 4 unter 100, ebenso 6 und 2 unter 1000 und 3 und 1 unter 10000 Ihren Platz erhalten. Dreht man nun das Rad 1, so werden sich zugleich die Räder 3, 6 und 5 einmal umdrehen und daher ebenso viele Einheiten, nämlich 36 500, dem Additionskästcben hinzufügen. Es ergibt sich also als Produkt im Ganzen:

      1460
     7300
   36500
   45260
Zu bemerken ist hier, dass am der größeren Bequemlichkeit willen die auf den Rädern des Multiplikanden befestigten Winden so anzupassen sind, dass die Räder sich bewegen müssen, wenn die Winden sich drehen, dass jedoch die Winden bei Drehung der Räder sich nicht zu bewegen brauchen. Denn sonst müssten sich, während sich ein Rad des Multiplikators (z. B. 1) dreht und damit alle Räder des Multiplikanden in Bewegung setzt, auch sämtliche Räder des Multiplikators (z. B. 2 und in 4) bewegen, was nur die Beschwerlichkeit erhöhen und die Bewegung verwirren würde.

Zu beachten ist auch, dass es gleichgültig ist, in welcher Reihenfolge die Räder des Multiplikators, 1, 2, 4 usw. angeordnet werden, dass sie jedoch ganz wohl in der Ordnung der Ziffern 1, 2, 3 usw. gestellt werden können. Denn trotzdem bleibt es einem überlassen, welches Rad man an erster oder zweiter Stelle umdrehen will. Dass das multiplizierende Rad, welches z. B. 9 darstellt oder welches im Durchmesser neunmal so groß sein muss als die entsprechende Winde, allzu groß wird, lässt sich dadurch umgehen, dass die entsprechende Winde umso kleiner gemacht wird, indem das richtige Verhältnis zwischen der Winde und dem multiplizierenden Rade gewahrt bleibt.

Damit bei der Anspannung der Sehnen und der Bewegung der Winden keine Unregelmäßigkeit entsteht, können anstatt der Sehnen auch kleine eiserne Ketten verwandt, und auf dem Umfang der Räder und Winden, in dem die Kette ruhen muss, messingene Zähnchen befestigt werden, die immer den einzelnen Gliedchen der Kette entsprechen müssen oder es können auch anstatt der Sehnen sowohl auf den Winden wie auf den multiplizierenden Rädern Zähne befestigt werden, so dass die Zähne des multiplizierenden Rades die Zähne der Winde unmittelbar berühren.

Wenn man die Maschine noch bewundernswerter machen wollte, so ließe es sich machen, dass die Drehung der Räder oder das Fortrücken der Multiplikationsmaschine von Operation zu Operation nicht von Menschenhand zu geschehen brauchte, indem man die Anordnung von vornherein so träfe, dass die Maschine alles von selbst besorgt. Allein dies würde die Maschine nur kostspieliger und umständlicher machen und vielleicht ihre Brauchbarkeit nicht erhöhen.

Schließlich habe ich noch über die Ausführung der Division in der Maschine einiges zu sagen, die freilich wohl noch niemand ohne jegliche geistige Arbeit allein mit der Maschine — bei großen Zahlen — zu Stande gebracht haben dürfte.

Aber was noch an Rechenarbeit bei unserer Maschine übrig bleibt, ist nicht zu vergleichen mit jenem verschlungenen Labyrinth der gewöhnlichen Divisionsmethode, dem langweiligsten Geschäft bei großen Zahlen und dem Unsichersten, was sich denken lässt.
Hier folgt also unsere Divisionsmethode. Es sei die Zahl 45260 durch 124 zu dividieren. Beginne wie gewöhnlich und suche den ersten einfachen Quotienten, oder wie oft 124 in 452 steckt. Es ist nun für jeden nur mäßig Geübten leicht, fast auf den ersten Blick den richtigen einfachen Quotienten zu vermuten. Es möge also 124 in 452 dreimal stecken. Mit diesem einfachen Quotienten multipliziere den ganzen Divisor 124, was mit leichter Mühe durch eine einfache Drehung des Rades geschieht. Das Produkt wird 372 sein. Dies ziehe von 452 ab; den Rest ziehe zu dem übrigen Dividenden 60. Daraus ergibt sich 8060.

Aber dies wird in der Maschine von selbst schon während der Multiplikation geschehen sein, wenn man den Dividenden zu Anfang in ihr einstellt, denn so wird jedes Ergebnis der Multiplikation von selbst von dem Dividenden abgezogen.

Die Subtraktion aber geschieht in der Maschine, während in ihr zu Anfang der Dividend hergestellt wird; denn die ausgeführten Multiplikationen werden von ihm abgezogen und immer der neue Dividend festgestellt nur von der Maschine selbst, ohne alle geistige Anstrengung.

8060 also teile wieder durch 124 und suche, wie oft 124 in 806 steckt. Jedem Anfänger ist es auf den ersten Blick klar, dass es sechsmal darin enthalten ist. Multipliziere nun 124 mit 6. Durch Drehung des einen multiplizierenden Rades 6 erhält man 744. Das Ergebnis ziehe von 806 ab, so bleibt als Rest 62. Zieht man dies zu dem noch übrigen Dividenden, so ergibt sich 620. Dieses dritte Produkt teile wieder durch 124. Es ist klar, dass 124 darin fünfmal steckt. Multipliziere 124 mit 5, so folgt 620. Zieht man dies von 620 ab, so bleibt nichts übrig. Also ist der Quotient 365.

Der Vorteil dieser Divisionsmethode vor der gewöhnlichen besteht vor allem darin (abgesehen von der Unfehlbarkeit), dass bei unserer Methode nur wenige Multiplikationen nötig sind, nämlich so viele, als Ziffern des ganzen Quotienten oder einfache Quotienten vorhanden sind; bei der gewöhnlichen Methode jedoch sind viel mehr nötig, nämlich so viele, wie Ziffern des Quotienten da sind, multipliziert mit der Ziffernzahl des Divisors. So waren in dem vorhergehenden Beispiel nach unserer Methode 3 Multiplikationen nötig, weil der ganze Divisor 124 mit den einzelnen Ziffern des Quotienten 365 multipliziert werden musste, deren Zahl 3 ist. Dagegen nach der gewöhnlichen Methode werden die einzelnen Ziffern des Divisors multipliziert mit den einzelnen des Quotienten, und daher ergeben sich in dem vorliegenden Beispiel 9 Multiplikationen.

Und es macht auch nichts aus, dass unsere wenigen Multiplikationen große sind, während auf dem gewöhnlichen Wege mehrere, aber kleine vorkommen; ebenso könnten ja auch, ließe sich ferner einwenden, bei der gewöhnlichen Methode wenige große nötig sein, wenn der ganze Divisor mit irgend einer Ziffer des Quotienten multipliziert werde. Aber die Antwort liegt ja auf der Hand, nämlich die, dass nach unserer Methode eine einzige große Multiplikation so leicht, ja sogar noch leichter ist als jede andere kleine. Denn sie geschieht schnell und durch eine einfache Drehung eines Rades, und zwar ohne alle Fehlergefahr. Dagegen je größer bei der gewöhnlichen Methode eine Multiplikation ist, desto schwieriger ist sie und der Fehlergefahr umso mehr ausgesetzt. Daher schien es denn den Lehrern der Arithmetik noch am besten, lieber viele kleine Multiplikationen als eine große beim Dividieren anzuwenden. Dazu kommt noch, dass der größte Teil der freilich schon so geringen Arbeit bei unserer Divisionsmethode darin besteht, die zu multiplizierende Zahl einzustellen, oder nach den Umständen die Zahl der beweglichen Zähne an den Rädern des Multiplikanden zu ändern. Aber hier beim Dividieren bleibt der Multiplikand (nämlich der Divisor) immer derselbe; es ändert sich nur der Multiplikator (nämlich der Quotient), ohne dass die Maschine verschoben zu werden braucht. Endlich kommt noch hinzu, dass die Mühe des Abziehens bei unserer Methode überhaupt wegfällt; denn während man in der Maschine multipliziert, ist die Subtraktion von selbst erledigt Hieraus erhellt, dass, je größer der Divisor ist, umso mehr der große Vorteil unserer Methode hervortritt.

Welche ausgedehnte Anwendung fernerhin diese Maschine finden wird, ist hinlänglich klar, denn die Beseitigung jeglichen Fehlers und aller oder doch fast aller Mühe aus der Zahlenrechnung ist von großem Nutzen sowohl im Staate, wie in der Wissenschaft. Es ist bekannt, mit welchem Beifall die Neper'schen Rechenstäbe aufgenommen wurden, und doch ist ihr Gebrauch weder viel schneller noch sicherer als die gewöhnliche Rechenmethode. Denn in Nepers Multiplikation sind fortwährende Additionen erforderlich, die Division aber geht um nichts leichter vonstatten als die gewöhnliche. Daher kamen denn auch die Rechenstäbe fast ganz außer Gebrauch. Dagegen in unserer. Methode erfordert das Multiplizieren gar keine, das Dividieren nur geringe Mühe.

Die Pascal‘sche Maschine ist immerhin ein Probestück des glücklichsten Genies, aber da sie nur die Addition und Subtraktion erleichtert, deren Schwierigkeit ohnehin nicht so groß ist, aber die Multiplikation und Division der früheren Rechnung überlässt, so hat sie sich mehr durch ihre Feinheit bei neugierigen als durch praktischen Nutzen bei ernst beschäftigten Leuten empfohlen.

Aber da jetzt an die Rechenmaschine die letzte Hand angelegt ist, so darf man annehmen, dass sie allen erwünscht sein wird, die mit Berechnungen zu tun haben, wozu bekanntlich die Verwalter des Fiskus, die Verwalter fremder Gelder, Kaufleute, Feldmesser, Geographen, Seeleute, Astronomen gehören, und was von Fachleuten sonst der Mathematik bedarf.

Aber um mich auf den rein wissenschaftlichen Gebrauch zu beschränken, so können nun ohne große Mühe die alten geometrischen und astronomischen Tafeln verbessert und neue aufgestellt werden, mit Hilfe deren man alle Arten von Linien und Figuren, die beliebig zusammengesetzt oder unzusammenhängend und unbenannt und, ebenso sicher messen kann, wie wir jetzt nach den Arbeiten des Regiomontanus Winkel und nach denen Ludolphs von Köln den Kreis wie gerade Linien behandeln können. Wenn das wenigstens bei den hauptsächlichsten und öfter vorkommenden Linien und Figuren der Fall sein wird nach Aufstellung von Tafeln nicht nur der Sinus und Polygone, sondern auch der Ellipsen und Hyperbeln und übrigen wichtigeren Figuren, die durch Bewegung oder durch Punkte zu beschreiben sind, dann erst darf man annehmen, dass die Geometrie zum praktischen Gebrauch vollkommen sein wird.

Aber wenn auch die optische Darstellung oder die astronomische Bobachtung oder die mannigfaltige Zusammensetzung von Bewegungen 5 neue Figuren bringen, so wird es doch jedem leicht sein, sich sogleich eine Tafel herzustellen, um seine Betrachtungen mit größter Leichtigkeit und Sicherheit durchzuführen. Denn es ist bekannt aus dem Scheitern der Versuche, den Kreis zu quadrieren, dass die Arithmetik die sicherste Gewähr für die geometrische Richtigkeit bietet. Daher wird sich auch die Mühe lohnen, arithmetische Tafeln, wie die größere pythagoräische Tafeln der Quadrate, Kuben und anderer Potenzen, Tafeln der Kombinationen, Variationen und Progressionen aller Art so weit wie möglich auszudehnen und dadurch die allgemeine Arbeit zu erleichtern.

Auch der Fleiß der Astronomen wird sicherlich durch keine Beschwerde mehr auf die Probe gestellt, als die des Rechnens. Dies schreckt sie ab von der Aufstellung und Verbesserung von Tafeln, von der Anlage von Ephemeriden, der Ausführung von Hypothesen und den Beobachtungen untereinander. Denn es ist ausgezeichneter Männer unwürdig, ihre Zeit mit sklavischer Rechenarbeit zu verlieren, die mit Anwendung der Maschine jedem Beliebigen mit Sicherheit Übertragen erden kannte.
Aber diese Ausführungen über die Konstruktion und die Anwendung des geplanten Werkes dürften genügen; gewiss werden sie nach Vollendung desselben den Augen des Beschauers noch deutlicher werden.

Die Leibniz-Maschiine erforderte also auch nach Leibniz eigener Darstellung vom Benutzer noch "gestige Arbeit".
Die erste Maschine, deren Ablauf voll mechansiert war und bei der nach Ausführung einer Rechenoperation
alle drei Zahlen angezeigt werden, stammt von Pfarrer Phlipp Matthäus Hahn aus dem Jahr 1774.
Er baute vier Exemplare, von denen zwei erhalten sind. Dieses ist zu sehen im Technoseum Mannheim.

 

Rechenwerkzeug.de