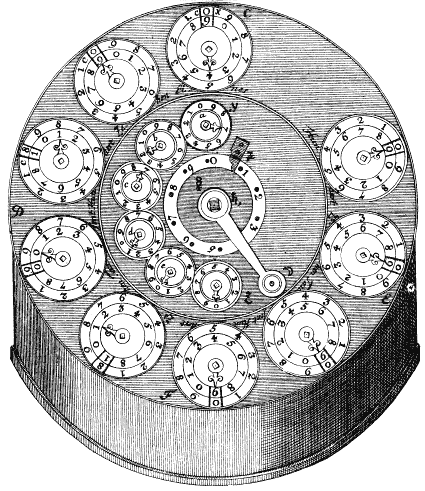
Die innere Skalenreihe stellt das Einstellwerk, die äußere das Resultatwerk dar. Wie das Einstellwerk, so ist auch Resultatwerk mit Zeigern zum Einstellen und Löschen versehen. Zur Addition stellt man auf dem Einstellwerk den ersten und auf dem Resultatwerk den zweiten Summanden ein. Dann dreht man die Kurbel zweimal im Gegenuhrzeigersinn und findet die Summe im Resultatwerk. Für die Subtraktion gibt es auf dem Resultatwerk eine Reihe mit Komplementärzahlen.

Bei Multiplikation und Division muss die Kurbel mehrfach gedreht werden und das Einstellwerk gegenüber dem Resultatwerk verstellt werden. Der Ring um die Achse der Kurbel mit den Zahlen 0 bis 9 stellt ein einstelliges Umdrehungszählwerk dar. Will man die auf dem Einstellwerk eingestellte Zahl mit 4 multiplizieren, so steckt man einen kleinen Stift in das Loch neben der 4 auf dem Ring und dreht die Kurbel so lange, bis der Stift beim Anschlag angekommen ist. Nach jeder Stelle muss der Ring manuell auf Null zurückgestellt werden.

In der Vorderansicht sieht man ganz oben die Einstellzeiger, darunter das Gehäuseblech, dann die Zahlenscheiben und darunter wieder die versetzt angeordneten Zahnräder. Ganz unten auf jeder Achse sitzt ein kleines Zahnrad. Dieses stellt die Verbindung zum Einstellwerk her.

Wie werden nun die Werte vom Einstellwerk ins Resultatwerk übertragen? Unter dem Zeiger jeder Stelle des Einstellwerks sitzt eine Schnecke (v) wie sie in Figur V abgebildet ist. Je nach Einstellung wird ein Hebel (l, m, n), der auf diese Schnecke im Punkt s aufliegt  angehoben oder abgesenkt. Dreht man nun an der Kurbel, so wird der in der Abbildung dunkler abgebildete Zahnkranz gegen den Uhrzeigersinn zwischen dem inneren und dem äußeren Werk hindurchgeführt. Auf diesem Zahnkranz ist ein langer Hebel mit einem Sägezahnsegment N beweglich montiert. Dieser trägt an der Stelle x eine kleine Treppe, wie sie in Figur IV in Vorderansicht gezeichnet ist. Der Die Zunge des Hebels n drückt an dieser Treppe das Zahnsegment nach außen und die Feder h drückt es wieder nach innen, sobald die Treppe die Zunge n passiert hat. Liegt der Hebel n tief, so wird das Zahnsegment über die ganze Breite der Treppe nach außen gedrückt und bewegt das Zahnrad J um neun Positionen weiter. Liegt der Hebel jedoch ganz oben, so wird die Treppe unter dem Hebel hindurchgeführt und das Zahnsegment N greift gar nicht in das Zahnrad J ein.
 

Leupold starb im Jahr 1727, noch vor Erscheinens seines Rechenmaschinen-Buches. Die von ihm erwähnte unvollendete Maschine gilt als verschollen. Ernst Martin ►L 5 schreibt 1925, dass "die Konstruktion nie zur Ausführung kam". Johann Paul Bischoff hatte zuvor schon in seinem 1804 erschienenen "Versuch einer Geschichte der Rechenmaschine" ►L 36 bezweifelt, dass der Zehnerübertrag bei Leupolds Maschine über mehrere Stellen hinweg funktionieren könne.  Jedoch existiert im Deutschen Museum eine Ausführung des Leupold-Entwurfs mit der Aufschrift "Braun invenit, Vayringe fecit". Anton Braun, ein Zeitgenosse Leupolds, der selbst eine Sprossenradmaschine konstruierte und baute, hat sie bei seinem Tod 1728 unvollendet hinterlassen, und Philipp Vayringe, ein lothringischer Uhrmacher, hat sie schließlich 1736 repariert und fertig gestellt. Mittlerweile existieren drei funktionsfähige Repliken.