Anleitung zum Arithmographe Troncet

(Original in Französosch hier)
1 Schachtel mit 12
Etuis für Notizminen 1 Franc 80
1 Schachtel mit 4 Etuis für
Notizminen 75 centimes
1 Schachtel mit 1 Bleistift mit Mine und 2
Etuis 1 Franc
ANLEITUNG ZUM ARITHMOGRAPHE
Beschreibung
Die Vorrichtung besteht im
Wesentlichen aus mehreren beweglichen Schiebern, die beziffert und
gezahnt mit einem festen Blech überzogen sind, in dem sich
kreisförmige Fenster und als Spazierstock geformte Rillen befinden.
Der
Zwischenraum der Zähne der beweglichen Schieber entspricht genau den zehn
Ziffern des Zahlensystems, die mehrmals in vertikalen Spalten auf dem festen
Blatt geschrieben sind.
Der Betrieb
Die Berechnungen
werden mechanisch mit Hilfe eines spitzen Stifts durchgeführt, der so fest
ist, dass er die beweglichen Schieber gleiten lässt.
Regel, Um eine Ziffernspalte zu
betreiben, platzieren Sie die Spitze in derjenigen Zahnlücke, die rechts von
der gesuchten Ziffer steht und ziehen sie bis zum unteren Ende der Rille,
wenn die Spitze zwischen weiß markierten Zähnen steht oder
nach oben, wenn auf einen schwarze Zähnr eingewirkt wird.
Operationen
Zu Beginn einer
Operation muss der Arithmographe auf Null stehen. Wir sagen, dass er
auf Null steht, wenn diese Ziffer in allen unteren Fenstern angezeigt wird,
mit Ausnahme desjenigen ganz links, in dem ein Leerzeichen angezeigt wird.
Auf Null werden die Schieber bis zum oberen Anschlag gefahren, wo ihre
Bewegung im Gerät begrenzt wird.
ADDITION
I. Was ist die Summe der Zahlen 8, 6, 5, 9?
 Wenn der Apparat auf Null steht, arbeiten Sie in der
ersten Spalte von rechts wie folgt: Platzieren Sie nacheinander die Spitze
des Stifts in der Verzahnung der beweglichen Schieber auf den rechten Seite
der 8, der 6, 5 und 9, und schieben Sie jedes Mal, bis zum Ende der Rille
entweder nach unten, wenn der Punkt zwischen die weißen Zähne fällt, oder
nach oben, wenn der Punkt zwischen die schwarzen Zähne fällt.
Wenn der Apparat auf Null steht, arbeiten Sie in der
ersten Spalte von rechts wie folgt: Platzieren Sie nacheinander die Spitze
des Stifts in der Verzahnung der beweglichen Schieber auf den rechten Seite
der 8, der 6, 5 und 9, und schieben Sie jedes Mal, bis zum Ende der Rille
entweder nach unten, wenn der Punkt zwischen die weißen Zähne fällt, oder
nach oben, wenn der Punkt zwischen die schwarzen Zähne fällt.
Die 28 erscheint sofort in den Ziffernfenstern am
unteren Rand der Schieber.
II. Addieren Sie die folgenden Zahlen: 24
Francs, 57 Francs und 876 Francs.
 Gehen Sie so vor, als ob Sie die angegebenen Zahlen
eingeben würden:
Gehen Sie so vor, als ob Sie die angegebenen Zahlen
eingeben würden:
24 steht für 2 in der Zehner- und 4 in der Einerspalte; 57
steht für 5 in der Zehnerspalte
und 7 in der Einerspalte und so weiter.
Der Gesamtbetrag von 957 wird angezeigt, sobald die Zahlen eingegeben sind.
III. Wir haben nacheinander 3,45 Francs, 6 Francs
und 2,75 Francs ausgegeben. Wie hoch ist der Gesamtaufwand?
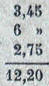 Durch Zuweisen der letzten beiden Spalten als
Dezimalstellen kommt die Einerstelle in die dritte Spalte
Durch Zuweisen der letzten beiden Spalten als
Dezimalstellen kommt die Einerstelle in die dritte Spalte
und wir lesen
12,20 als Summe.
SUBTRAKTION
Wenn das Gerät in den Additionsfenstern Null zeigt, sehen wir in den Subtraktionsfenstern die Ziffer 9. Schreiben Sie zuerst die größer Zahl in die Subtraktionsfenster. Platzieren Sie dazu die Spitze rechts neben der höchsten Zahl 9 und bewegen Sie den Schieber nach unten, bis die einzugebende Zahl in den Subtraktionsfenstern erscheint. Dann geben Sie die kleine Zahl nach der allgemeinen Regel ein und die Differenz erscheint in den Subtraktionsfenstern.
I. Ziehen Sie 3 von 7 ab.
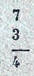 Geben Sie die große Zahl ein, indem Sie die Spitze des
Stifts rechts von der Teilung 9 und nach unten schieben, bis die 7 im
Subtraktionsfenster erscheint. Die kleine Zahl 3 wird gemäß der Regel
registriert, und der Rest 4 wird sofort in den Subtraktionsfenstern
angezeigt.
Geben Sie die große Zahl ein, indem Sie die Spitze des
Stifts rechts von der Teilung 9 und nach unten schieben, bis die 7 im
Subtraktionsfenster erscheint. Die kleine Zahl 3 wird gemäß der Regel
registriert, und der Rest 4 wird sofort in den Subtraktionsfenstern
angezeigt.
II. Was bleibt von 85 Francs, wenn wir
nacheinander 25 Francs und 14,75 Francs wegnehmen?
In der Praxis würden wir hier zwei Dinge tun; Der
Arithmograph hat den Vorteil, dass er nur eine Operation ausführt. Geben Sie
die größte Zahl wie im vorigen Beispiel gefolgt von zwei Nullen (8500)
ein, danach die beiden anderen Beträge durch das übliche Verfahren, um die
Zahlen zu subtrahieren, und lesen Sie die Differenz 45,25 in den
Subtraktionsfenstern.
Grauer Kreis
Wenn in einem
Fenster anstelle einer Zahl ein grauer Kreis angezeigt wird, müssen Sie sich
darüber keine Gedanken machen. Wenn es jedoch anhält, könnte es zu
einem Ärgernis werden. Der Bediener wird aus Erfahrung sehr schnell
beurteilen, ob es nützlich ist, ihn zu verfolgen. Es versteht sich von
selbst, dass Sie den grauen Kreis verfolgen müssen, um ein Ergebnis zu
lesen. Um dies zu tun, platzieren Sie die Spitze unten in der 0-Teilung und
gehen Sie bis zum anderen Ende des Stocks.
Warnung
Dieses
Gerät verarbeitet sieben Stellen: es liefert genaue Ergebnisse bis zu 10 000
000. Wenn man diese Grenze überschreitet oder auf dem Gerät
eine unmögliche Berechnung ausführt (z.B. subtrahieren 36 von 24), erscheint
im letzten Fenster links ein schwarzer Kreis als Warnanzeiger.
 Die folgenden Tabellen enthalten eine Reihe von Zahlen, bei denen es
genügt, sie auf dem Arithmographen zu addieren oder zu subtrahieren, um eine
Multiplikation oder Division durchzuführen. Alle Zahlen von 0 bis 999 sind
der Reihe nach in verschiedene Fächer eingeschrieben; man sieht also
nacheinander die Fächer 50, 51, 52 usw. Alle Fächer sind untereinander
ähnlich: bei jedem steht oben die Hauptzahl fettgedruckt, links reihen sich
vertikal die neun bezeichnenden Ziffern in Kursivdruck und rechts, nach
einem Trennungspunkt, liest man das Produkt der Hauptzahl mit jeder von
ihnen. Untersuchen wir beispielsweise das Fach 53. Das Produkt von 53 und 1
ist die Zahl 53 selbst, die wir jetzt neben der Ziffer 1 sehen; das Produkt
aus 53 und 2 ist 106, wie es nach der Ziffer 2 geschrieben steht, etc.
Die folgenden Tabellen enthalten eine Reihe von Zahlen, bei denen es
genügt, sie auf dem Arithmographen zu addieren oder zu subtrahieren, um eine
Multiplikation oder Division durchzuführen. Alle Zahlen von 0 bis 999 sind
der Reihe nach in verschiedene Fächer eingeschrieben; man sieht also
nacheinander die Fächer 50, 51, 52 usw. Alle Fächer sind untereinander
ähnlich: bei jedem steht oben die Hauptzahl fettgedruckt, links reihen sich
vertikal die neun bezeichnenden Ziffern in Kursivdruck und rechts, nach
einem Trennungspunkt, liest man das Produkt der Hauptzahl mit jeder von
ihnen. Untersuchen wir beispielsweise das Fach 53. Das Produkt von 53 und 1
ist die Zahl 53 selbst, die wir jetzt neben der Ziffer 1 sehen; das Produkt
aus 53 und 2 ist 106, wie es nach der Ziffer 2 geschrieben steht, etc.
Gesucht sei das Produkt aus 279
und 5.827.
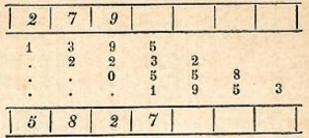

ALLGEMEINE BEMERKUNGEN
Die Zifferstreifen in ihren Rillen hin- und
hergleiten lassen, das ist das einzige Mittel, das hier angewendet wird, um
Rechnungen auszuführen. Dieses Mittel für Rechenoperationen ist einfach und
sicher und für alle Menschen verfügbar. Jeder kann es anwenden und seine
Genauigkeit überprüfen, ohne irgendein Spezialstudium in Mathematik gemacht
zu haben.
Indem man sich an die Hinweise für den
Gebrauch hält, kommt man sehr schnell dahin, dass man den Apparast
flüssig bedienen kann; dennoch ist es gut, die vorliegenden Bemerkungen zu
berücksichtigen, wenn man Wert darauf legt, am Anfang unnötiges Herumtasten
zu vermeiden.
Der Stift
Der Stift des Arithmographen hat eine doppelte
Spitze: eine Minenspitze und eine abgerundete Spitze. Indem man die
Minenspitze zwischen Daumen und Zeigefinger dreht, lässt man die Mine je
nach Wunsch herauskommen oder zurückgehen, mit deren Hilfe man auf dem
Schieferpapier schreiben kann. Die abgerundete Spitze dient dazu, in dem
Apparat die beweglichen und mit Zähnen versehenen Streifen auf- und
abgleiten zu lassen.
Das Gleiten
Die ganze Fertigkeit des Benutzers hängt von seiner Geschicklichkeit ab, die abgerundete Spitze einzusetzen und damit die Streifen zu verschieben. Anfänger tun gut daran, die folgenden Vorbereitungsübungen ein paar Mal zu wiederholen.
Gleiten nach unten: Stecken
Sie die abgerundete Spitze des Stiftes zwischen zwei weißen Zähnen eines
Zifferstreifens ein und ziehen Sie damit nach unten, in gerader Linie, bis
ans Ende der Öffnung.
Gleiten nach oben: Stecken
Sie die Spitze des Stiftes zwischen zwei schwarzen Zähnen eines Streifens
ein und schieben Sie sie nach oben, folgen Sie dabei der Kurve bis zum Ende
der Öffnung des Kreuzstabes.
ZUSATZBEMERKUNG: Der Stift muss fast senkrecht
zur Oberfläche des Rechners gehalten werden. Die abgerundete Spitze soll in
einer stetigen Bewegung auf der Grundfläche des Apparates gleiten, bis zu
einem der Enden des Kreuzstabes, wo sie anschlägt und ihren Lauf beendet.
Einstellen auf Null
Vor jeder Rechenoperation steht der
Arithmographe auf Null, das heißt alle Zifferstreifen sind am Ausgangspunkt
im oberen Teil des Apparates. Um die Streifen auf Null zu stellen, muss man
sie also wieder hochschieben bis zu ihrem natürlichen Haltepunkt, der durch
den oberen Rand des Rechners gebildet wird. Um jeden Streifen völlig wieder
hochzuschieben, und zwar in einer einzigen Bewegung, steckt man die
abgerundete Spitze in die untersten Abteilungen, möglichst in die mit der
Bezeichnung 0. Der Anzeigestreifen (erster von links) muss dann einen
Leerraum anzeigen. Wenn dort eine schwarze Fläche erscheint, schiebt man sie
nach oben, indem man auf den Zahn drückt, der sich links von der Ziffer 9 in
der ersten Zahlenreihe zeigt.
Rechenoperationan
Um gut vorzugehen, genügt es, ohne Zögern auf
dem Arithmographen die Zahl zu finden, die man braucht, die abgerundete
Spitze in die Zahnradhöhlung rechts von dieser Zahl zu setzen und dann bis
zu einem Ende des Kreuzstabes gleiten zu lassen, entweder nach unten, wenn
es sich um einen weißen Zahn handelt, oder nach oben, wenn man an dem
schwarzen Zahn angesetzt hat. Ausnahmsweise schreibt man bei einer
Subtraktion die Ziffern der größeren Zahl, indem man die Gummispitze in die
Abteilung 9 setzt und dann nach unten schiebt bis zu der Zahl, die man
einschreiben will.
Anordnung der Zahlen
Die Zahlenkolonnen des Arithmographen werden
ohne Unterscheidung der verschiedenen Ordnungen der Dezimalzahlenfolge
angewendet. Wenn man also ganze Zahlen addiert, kann die erste Spalte von
rechts die Einer aufnehmen, die zweite die Zehner usw. Der Name der
Reihenfolge wird bei Bedarf auf einem der Notizstreifen notiert. Ein
Beispiel:

Man sieht auf obiger Tabelle, wie sich die
Ziffern einer Zahl, in diesem Fall 23.257, leicht in ihre betreffenden
Spalten eintragen lassen.
Wenn man mit Dezimalzahlen operiert, etwa Francs und Centimes, kann man auf den Notizstreifen folgenden Hinweis eintragen

Normalerweise setzt man nur einen Punkt, um die
Einheitenklassen zu bezeichnen, und ein Komma, um den ganzzahligen Teil von
dem Dezimalteil der Zahl abzugrenzen.
Man muss dazu bemerken, dass man im Allgemeinen
die Zahlen so einträgt, wie man sie ausspricht, indem man mit den größten
Einheiten anfängt und mit den kleinsten aufhört. Aber man kann sie auch so
aufschreiben, dass man einer ganz anderen Richtung folgt. Man kann
ebenfalls, wenn es nützlich erscheint, eine begonnene Operation unterbrechen
und sie später erst fortführen. Der Arithmographe sichert verlässlich das
Ergebnis der Rechenoperation, so lange bis man es auslöscht, indem man alles
wieder auf 0 stellt.
Rechenwerkzeug.de