Auszug aus dem Buch von Adam Riese

Rechenbuch /auff Linien und Ziphren/ in allerley Handthierung Geschäfften unnd Kauffmannschaft.

Rieses Rechentafel ist - ähnlich dem Stschoty und im Gegensatz zum römischen Abakus - in Zeilen aufgebaut. Der Stellenwert jeder Zeile steigt von unten nach oben jeweils um den Faktor 10. Ähnlich dem römischen Zahlensystem werden Rechenmünzen eingespart, indem Münzen in den Zwischenräumen der fünffache Wert der Münzen auf der darunterliegenden Linie zugewiesen wird.

Um zwei Zahlen zu addieren, legt man zuerst die eine, dann die andere Zahl auf das Brett. anschließend wird bereinigt. Fünf Münzen auf einer Linie werden dabei gegen eine Münze im darüber liegenden Zwischenraum getauscht, zwei Münzen im gleichen Zwischenraum durch eine Münze auf der nächsthöheren Linie. Danach kann das Ergebnis abgelesen werden.

Statt in Euro und Cent rechnete man zu Adam Rieses Zeiten unter anderem mit Gulden (fl), Groschen (gr) und Pfennigen oder Hellern (dl). Hierfür benötigte das Rechenbrett drei Spalten, in denen auch von rechts nach links bereinigt wurde: 12 Heller wurden hier gegen einen Groschen, 21 Groschen gegen einen Gulden getauscht. 

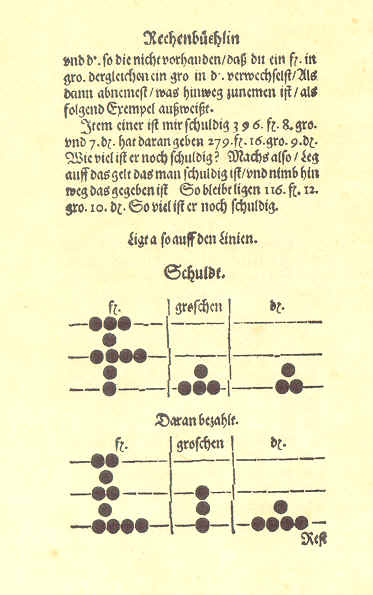
Auf dieser Doppelseite ist ein Subraktionsvorgang abgebildet. In der rechten Spalte der Abbildung sollen von 7 Hellern ("Schuldt") 9 Heller ("Daran bezahlt") subtrahiert werden. Das geht nicht. Deshalb muss zunächst aus der mittleren Spalte ein Groschen weggenommen werden und der rechten Spalte dafür 12 Heller hinzugefügt werden. Zusammen mit den vorhandenen 7 Hellern ergeben sich 19 Heller. Von diesen werden die 9 Heller Schulden weggenommen. Zehn Heller bleiben übrig ("Rest noch").
Von den 8 abgebildeten Groschen ("Schuldt") sind nur noch 7 vorhanden. Davon sollen 16 Groschen ("Daran bezahlt" abgezogen werden. Dies geht nur, wenn man einen Gulden der linken Spalte in 21 Groschen umtauscht. 7+21 = 28; 28 - 16 = 12 Groschen ("Rest noch"). In der linken Spalte sind schließlich von den noch vorhandenen 395 Gulden ("Schuldt") 279 Gulden ("Daran bezahlt") abzuziehen. Das ergibt 116 Gulden ("Rest noch").

Um eine gelegte Zahl zu verdoppeln ("Duplirn") werden beginnend von oben Münzen aus den Zwischenräumen auf die nächst höhere Linie gezogen: So wird z.B. aus einer Mpnze mit dem Wert 500 eine Münze mit dem Wert 1000. Münzen, die auf Linien liegen werden verdoppelt. Wo auf einer Linie drei Münzen lagen, liegen danach 6. Die aber sind zu bereinigen: 5 davon sind wegzunehmen und stattdessen eine Münze in den darüber befindlichen Zwischenraum zu schieben.
Halbiert ("Medirn") wird von unten nach oben, dabei wird immer eine Linie zusammen mit dem darüber liegenden Zwischnraum betrachtet. Liegen auf der untersten Linie drei Einer und darüber ein Fünfer, so ersetzt man sie durch vier Einer. Liegen nur zwei Einer und ein Fünfer dort, so halbiert man 6 zu drei Einern auf die Linie und schiebt den siebten nicht teilbaren Einer in den Zwischenraum unter die Linie.

Multiplizieren erfolgt analog zum Verdoppeln. Dazu muss man nun das kleine Einmaleins kennen. Will man zum Beispiel 6 (ein Fünfer und ein Einer) vervierfachen, so nimmt man die beiden Münzen weg und ersetzt sie durch zwei Zehner und vier Einer.
Íst der zweite Faktor mehrstellig (z.B. bei 6 mal 24), so führt man zunächst die Multiplikation mit 4 aus, man nimmt die 6 weg und legt 24 dafür, danach multipliziert man die 6 im Kopf mit 20, d.h. man verdoppelt sie zu 12 und legt diese 12 aber stellenverschonen als 1 Hunderter und 2 Zehner ab. 

Division erfolgt nach einem ähnlichen Verfahren, wie man schriftlich rechnet: Wenn eine Zahl, die 6 Tausender enthält, durch 3 geteilt werden soll, so nimmt man die 6 weg und legt 2 dafür hin. Wenn man anschließend die 7 Hunderter durch 3 teilt, bleibt 1 Hunderter als nicht teilbar übrig. Dieser wird in Gestalt von 2 Fünfzigern in die nächsten Stelle heruntergezogen und dort berücksichtigt.

Hier geht's zu den Rechenpfennigen

Rechenwerkzeug.de