Der Proportionalzirkel
Freie Übersetzung aus «De l'usage du compas» (Paris 1688) von Jacques Ozanam, 1640-1718
 Die ersten Beschreibungen des Proportionalzirkels
("Gebrauch und Herstellung eines Zirkels bestimmter Maße, mit dem fast alle
Probleme der euklidischen Mathematik gelöste werden können") wurden 1606 von Galilei und
1607 von Baldassare Capra aus Padua veröffentlicht. Aber schon etwa 1568 hatte
ein Freund Galileis, Guidobaldo del Monte, ein ähnliches Werkzeug in
Gebrauch. Dieses Gerät, das sich seit seinem Ursprung nur noch sehr wenig
weiterentwickelt hat, wurde im 17. und 18. Jahrhundert und auch noch bis zum
Ende des 19. Jahrhunderts sehr häufig verwendet. Es war auf die Bedürfnisse
von Ingenieuren, Geometern, Artilleristen und allen Arten von Handwerkern abgestimmt,
da man damit auf graphische Weise Berechnungen durchführen konnte, die numerisch
kompliziert gewesen wären.
Die ersten Beschreibungen des Proportionalzirkels
("Gebrauch und Herstellung eines Zirkels bestimmter Maße, mit dem fast alle
Probleme der euklidischen Mathematik gelöste werden können") wurden 1606 von Galilei und
1607 von Baldassare Capra aus Padua veröffentlicht. Aber schon etwa 1568 hatte
ein Freund Galileis, Guidobaldo del Monte, ein ähnliches Werkzeug in
Gebrauch. Dieses Gerät, das sich seit seinem Ursprung nur noch sehr wenig
weiterentwickelt hat, wurde im 17. und 18. Jahrhundert und auch noch bis zum
Ende des 19. Jahrhunderts sehr häufig verwendet. Es war auf die Bedürfnisse
von Ingenieuren, Geometern, Artilleristen und allen Arten von Handwerkern abgestimmt,
da man damit auf graphische Weise Berechnungen durchführen konnte, die numerisch
kompliziert gewesen wären.
Der Proportionalzirkel besteht aus zwei flachen Linealstäben, die die Schenkel eines Winkels bilden und an einer Schmalseite mit einem flachen Scharnier verbunden sind. Dieses ist so angelegt, dass der Zirkel sich vollkommen öffnen lässt, so dass er dann ein gerades Lineal bildet. Vom Zentrum des Scharniers gehen einige auseinanderstrebende gerade Linien aus, immer zwei und zwei identisch, symmetrisch zur Öffnungsachse des Instruments.
Das Gebrauchsprinzip besteht darin, die Schenkel zu öffnen
und die Eigenschaften ähnlicher Dreiecke zu nutzen. Mit Hilfe eines Stechzirkels
überträgt man zunächst die betreffenden Größen zwischen zwei identische Markierungen
eines Skalenpaars auf den beiden Schenkeln. Dann misst man an einer anderen
Stelle der Skalen zwischen zwei weiteren identischen Markierungen eine die gesuchte
Größe ab. Je nach der verwendeten Skala kann man so direkt Streckenlängen oder
Winkel bestimmen.
Mit weiteren Skalen kann man Aufgaben zum Gewicht oder das
Volumen von Metallen lösen oder den Durchmesser
von Artilleriegeschossen bestimmen.
Klassischerweise sind die Skalen auf jedem Schenkel 6 Pouces (Daumen), also einen halben Fuß lang, so dass das Instrument in voller Länge einen Fuß misst. Wenn es sich dabei um das ab 1668 in Frankreich geltende Maße handelt, erhält man mit 32,4839 cm einen „Königsfuß“. Die damals üblichen Längenmaße (allerdings in verschiedenen Provinzen unterschiedlich groß), waren
-
1 Punkt = 1/12 der Dicke eines mittleren Gerstenkorns
-
1 Linie = 12 Punkte, also die Dicke eines mittleren Gerstenkorns
-
1 Daumen = 12 Linien
-
1 Fuß = 12 Daumen.
Die mit Einteilungen versehenen Skalen
Die Lage der Skalen in Beziehung zueinander ist im Prinzip immer die gleiche: Sie ist festgelegt durch den Gebrauch des Instruments: Danach findet man auf der Vorderseite von außen nach innen die Linie der gleichen Teile (Parties Egales), die der ebenen Figuren (Les Plans) und die der gleichseitigen Vielecke (Les Poligones). Auf der Rückseite sind von außen nach innen die Linie der Sehnen (Les Cordes) verwendbar als Winkelmesser, die der Körper (Les Solides) und die der Metalle (Les Metaux) aufgetragen. Manche Instrumente enthalten noch andere Gradeinteilungen, bei anderen fehlen die Linie der ebenen Figuren und die der Körper.
Vorderseite

Die Linie der gleichen Teile (Les Parties Egales)
ist in 200 gleiche Teile eingeteilt und in Zehnerschritten nummeriert. Sie dient dazu, arithmetische Aufgaben zu lösen, etwa um eine gegebene Länge proportional zu vergrößern oder zu verkleinern, oder sie in gleiche Teilstücke oder zueinander proportionale Teile zu zerlegen.
Die Linie der ebenen Figuren (Les Plans, auf Abbildung unbezeichnet)
ist in 64 Teilstriche eingeteilt und in Zehnerschritten nummeriert. Es ist eine Skala, die mit dem Quadrat des Abstands zum Ursprung im Zentrum des Zirkels nummeriert ist. Diese Skala erlaubt es, Aufgaben zu lösen, die mit Flächen zu tun haben, z.B. eine ebene Figur in eine doppelt so große ähnliche Figur zu verwandeln.
Die Linie der Vielecke (Les Poligones)
umfasst 10 Gradeinheiten, die von 3 bis 12 nummeriert sind. Sie gibt die Länge der Seiten der zehn ersten regelmäßigen Vielecke an, die in einen Kreis mit gegebenem Durchmesser eingezeichnet werden können.
Die Linie der Geschosskaliber (Calibre des Pieces)
dient zur Bestimmung des Durchmessers von eisernen Kanonenkugeln.
Rückseite

Die Linie der Sehnen (Les Cordes)
ist in 180 Teile eingeteilt, die in Zehnerschritten nummeriert sind. Die Gradeinteilungen sind proportional zum Kosinus der Skalenwerte. Die Skala erlaubt es, Winkel zu messsen und Winkel mit gegebener Gradzahl zu zeichnen.
Die Linie der geometrischen Körper (Les Solides)
ist in 64 Teile eingeteilt, ebenfalls in Zehnerschritten nummeriert. Sie ist mit der dritten Potenz des Abstands jeder Teilung zum Zentrum des Zirkels beziffert. Die Skala erlaubt es z.B., zu einem gegebenen Körper einen Körper mit doppelt oder halb so großem Volumen zu konstruieren.
Die Linie der Metalle (Les Metaux)
umfasst 6 Gradeinteilungen, die bezeichnet sind mit den astronomischen Symbolen für die sechs gebräuchlichsten Metalle in der Reihenfolge ihrer Dichte. Von den äußeren Spitzen des Zirkels zum Zentrum hin findet man hier: Jupiter für Zinn, Mars für Eisen, Merkur für Kupfer, Mond für Silber, Saturn für Blei und Sonne für Gold. Die Entfernungen von jeder Gradeinteilung zum Zentrum des Proportionalzirkels sind umgekehrt proportional zur Kubikwurzel der Dichte dieser Metalle. Mit Hilfe dieser Skala kann man Aufgaben lösen, die das Gewicht, das Volumen oder die Zusammensetzung der Legierung von Metallen betreffen.
Die Linie des Gewichtes von Eisenkugeln (Poids de Boulets),
dient zur Umrechnung der von Volumen und Gewicht bei verschiedenen großen Eisenkugeln. Diese Linie wird ebenso wie die Linie Calibre des Pieces auf der anderen Seite bei vollständig geöffnetem Instrument verwendet.
 Der Hersteller des abgebildeten Proportionalzirkels, Michel Grilliet wurde
1743 geboren und betrieb eine Uhrmacherwerkstatt in Paris.
Der Hersteller des abgebildeten Proportionalzirkels, Michel Grilliet wurde
1743 geboren und betrieb eine Uhrmacherwerkstatt in Paris.
Einige Anwendungsbeispiele
Im Allgemeinen benutzt
man de Proportionalzirkel in Verbindung mit einem Stechzirkel. Mit diesem greift
man ein gegebenes Maß ab und überträgt es auf den Proportionalzirkel zwischen
zwei identische Gradeinteilungen von der gleichen Linienart auf die Schenkel,
die man entsprechend öffnet. Danach misst man mit dem Stechzirkel zwischen zwei
anderen identischen Gradeinteilungen derselben Linie die gesuchte Größe ab,
wobei man die Öffnung des Proportionalzirkels beibehält.
Linie der gleichen Teile (Parties Egales)
1. Addition oder Subtraktion von Strecken mit gegebenem Maß:
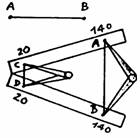 Wenn
AB 140 Einheiten misst, wie groß ist dann die Strecke CD mit 20 Einheiten?
Wenn
AB 140 Einheiten misst, wie groß ist dann die Strecke CD mit 20 Einheiten?
Nachdem
man mit dem Stechzirkel das Maß von AB abgenommen hat, wird dieses Maß zwischen
den zwei Gradeinteilungen 140 der Linie der gleichen Teile übertragen und die
zwei Schenkel des Proportionalzirkels entsprechend geöffnet. Mit den Spitzen
des Stechzirkels übernimmt man dann das Maß zwischen den zwei Einheiten 20 der
Linie der gleichen Teile auf dem Proportionalzirkel, der immer noch so weit
geöffnet ist wie vorher. Das ist die Länge der gesuchten Strecke CD.
2. Teilen eines Geradensegments in gleiche Teile oder Vergrößerung eines solchen Segments:
Zu finden ist der 7. Teil der Strecke AB.
Man trägt AB zwischen den identischen Gradeinteilungen eines Vielfache von 7 (beispielsweise 140) ein. Nun nimmt man die Länge des 7. Teils zwischen den identischen Gradeinteilungen des Werts 140/7, also 20.
Mit dem umgekehrten Verfahren kann man auch CD vergrößern.
3. Maß der Seiten eines Vielecks, von dem eine Seite bekannt ist:
Wenn AB 140 Einheiten misst, wie lang ist dann CD?
Man trägt AB zwischen den identischen Markierungen 140 ab, sucht die Markierungen, die dem Maß von CD entsprechen, die man mit dem Stechzirkel abgenommen hat, und die Zahl, die diese Gradabstufungen charakterisiert, ist der gesuchte Wert.
4. Einteilung eines Geradenabschnitts (ähnlich wie Fall 2, aber nicht zu verwechseln mit Fall 5):
Es sind 2/7 oder 20/70 von AB zu markieren.
Man nimmt AB zwischen den identischen Gradabstufungen 70 ab, dann misst man die Länge der 2/7 zwischen den Gradabstufungen 20.
5. Teilung eines Geradenabschnitts in proportionale Teile
AB ist in zwei Teilstücke zu teilen, die zueinander im Verhältnis 2:7 stehen sollen.
2 + 7 = 9 (oder 20 + 70 = 90) AB wird zwischen den identischen Gradeinteilungen 90 abgenommen, dann wird das Maß zwischen den Gradabstufungen 20 oder 70 bestimmt und von dem einen oder anderen Endpunkt der Strecke aus abgetragen.
Für alle
diese Operationen gilt: Wenn AB zu lang ist, um zwischen die zwei Schenkel des
Proportionalzirkels zu passen, reicht es aus, mit einem beliebigen Bruchteil
von AB zu operieren (1/4, 1/1000...) und das Ergebnis mit dem entsprechenden
Faktor zu multiplizieren (4, 1000...)
Linie der ebenen Figuren (Les Plans)
Vielecke sind in Dreiecke zu zerlegen, so dass man mit ähnlichen Seiten arbeiten kann. Bei Kreisen arbeitet man mit dem Durchmesser.
6. 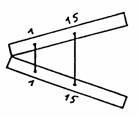 Vergrößerung
oder Verkleinerung einer Vieleck- oder Kreisfläche
Vergrößerung
oder Verkleinerung einer Vieleck- oder Kreisfläche
Ein Dreieck ist so zu verändern, dass seine Fläche 15fach vergrößert wird.
Man trägt die erste Seite zwischen den beiden Gradeinteilungen 1 ab. Dann misst man die entsprechende Seite zwischen den beiden Gradeinteilungen 15 und verfährt entsprechend weiter für die anderen Seiten. Umgekehrt kann man, statt zu vergrößern, entsprechend verkleinern.
7. 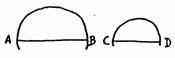 Beziehung zwischen zwei ähnlichen Vieleck- oder Kreisflächen
Beziehung zwischen zwei ähnlichen Vieleck- oder Kreisflächen
Wie ist das Verhältnis der Flächen der Kreise AB und CD?
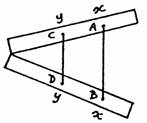 Bei einer beliebigen Öffnung des Proportionalzirkel werden die zwei Durchmesser
zwischen identischen Gradeinteilungen bei x und y abgetragen. Das Verhältnis
zwischen den Zahlen dieser Gradeinteilungen y und x ist das gesuchte. (Wenn
es möglich ist, öffnet man den Proportionalzirkel so, dass x und y ganze Zahlen
sind.)
Bei einer beliebigen Öffnung des Proportionalzirkel werden die zwei Durchmesser
zwischen identischen Gradeinteilungen bei x und y abgetragen. Das Verhältnis
zwischen den Zahlen dieser Gradeinteilungen y und x ist das gesuchte. (Wenn
es möglich ist, öffnet man den Proportionalzirkel so, dass x und y ganze Zahlen
sind.)
Hinweis: Wie bei den gleichen Teilen kann man auch hier mit Bruchteilen der Seiten oder Durchmesser operieren.
Linie der Vielecke (Les Poligones)
8. Konstruktion eines regelmäßigen Vielecks in einen Kreis mit gegebenem Radius
Der gegebene Radius wird zwischen den Gradeinteilungen 6 abgetragen (und zwar für alle Arten von Vielecken). Danach wird die Seite des Vielecks zwischen den identischen Gradeinteilungen, die es charakterisieren (3 für Dreieck, 4 für Quadrat...) abgemessen und entlang der Kreislinie abgetragen.
9. Zeichnen eines regemäßigen Vielecks mit Hilfe einer Strecke, die als Seite gegeben ist
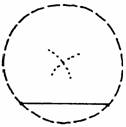 Zunächst
muss man die Länge des Geradenabschnitts zwischen den Gradeinteilungen messen, die das
geplante Vieleck charakterisieren. Dann wird zwischen den Gradeinteilungen 6
das Maß des Radius desjenigen Kreises abgenommen, in den man dieses Vieleck
einzeichnen kann. Von jedem Ende der gegebenen Strecke zeichnet man nun zwei
Kreisbögen, die als Radius die oben beschriebene Strecke haben: Ihr Schnittpunkt
ist der Mittelpunkt des Umkreises, in den das Vieleck eingezeichnet wird. Dieser
Kreis wird nun gezeichnet und dann nacheinander die übrigen Seiten eingezeichnet.
Zunächst
muss man die Länge des Geradenabschnitts zwischen den Gradeinteilungen messen, die das
geplante Vieleck charakterisieren. Dann wird zwischen den Gradeinteilungen 6
das Maß des Radius desjenigen Kreises abgenommen, in den man dieses Vieleck
einzeichnen kann. Von jedem Ende der gegebenen Strecke zeichnet man nun zwei
Kreisbögen, die als Radius die oben beschriebene Strecke haben: Ihr Schnittpunkt
ist der Mittelpunkt des Umkreises, in den das Vieleck eingezeichnet wird. Dieser
Kreis wird nun gezeichnet und dann nacheinander die übrigen Seiten eingezeichnet.
Linie der Sehnen (Les Cordes)
10.
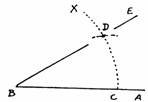 Zeichnung
eines Winkels von gegebenem Wert
Zeichnung
eines Winkels von gegebenem Wert
Ein Winkel von 40° ist von B aus zu zeichnen. Mit B als Mittelpunkt wird ein beliebiger Kreis CX gezogen. Der Proportionalzirkel wird so weit geöffnet, dass der Radius des Kreises zwischen die Gradeinteilungen 60 passt. Dann wird die Länge zwischen den Gradeintielungen 40 abgenommen und sie auf D übertragen, wobei C als Mittelpunkt genommen wird. Der Winkel ABD beträgt nun 40°.
11. Maß eines gegebenen Winkel bestimmen
Vom Scheitelpunkt
B aus zeichnet man einen beliebigen Kreisbogen CX, der die Strecke BE in D schneidet.
Der Radius dieses Kreises wird zwischen den Gradabstufungen 60 abgetragen. Danach
greift man die Länge von CD ab und sucht die identischen Gradeinteilungen, die
ihr entsprechen: Die Zahl dieser Gradeinteilungen ist der gesuchte Wert.
Linie der Körper (Les Solides)
Wenn es sich um Parallelflächner handelt, arbeitet man mit den Kanten. Wenn es sich um Kugeln handelt, arbeitet man mit dem Durchmesser.
12. Vergrößerung oder Verkleinerung eines Parallelflächners oder einer Kugel
Ein rechtwinkliger Parallelflächner mit dem Inhalt 3 soll auf den Inhalt 5 vergrößert werden.
(Um exakter arbeiten zu können, benutzen wir hier 30 und 50 anstelle von 3 und 5.)
Man trägt die erste Kante zwischen den Gradabstufungen 30 ab. Dann nimmt man die entsprechende Kante zwischen den Gradabstufungen 50 ab und verfährt bei den anderen Kanten genauso.
13. Verhältnis zwischen zwei ähnlichen geometrischen Volumen
Man arbeitet
nach demselben Prinzip wie in 7. und wendet es hier auf die Linie der Körper
an.
Linie der Metalle (Les Metaux)
14. Gegeben ist der Durchmesser einer Kugel aus einem bestimmten Metall mit bekanntem Gewicht. Gesucht wird der Durchmesser einer Kugel gleichen Gewichts aus einem anderen Metall.
Man trägt den bekannten Durchmesser zwischen den beiden Gradabstufungen ab, die für dieses Metall gegeben sind (Sonnensymbol für Gold etc.) Dann liest man den gesuchten Durchmesser zwischen den beiden Gradeinteilungen für das gewünschte Metall ab.
15.
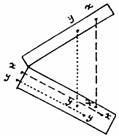 Das
Verhältnis der Gewichte entsprechend dem gleichen Volumen verschiedener Metalle
Das
Verhältnis der Gewichte entsprechend dem gleichen Volumen verschiedener Metalle
Man nimmt die Entfernung vom Zentrum des Proportionalzirkels bis zu der Gradeinteilung, die das leichteste Metall bestimmt und überträgt sie als x;x) zwischen zwei beliebige identische Gradeinteilungen auf der Linie der Körper (Les Solides). Dann misst man die Entfernung vom Zentrum des Proportionalzirkels bis zu der Gradeinstellung, die das schwerere Metall bestimmt. Darauf sucht man auf der Linie der Körper, welcher Gradeinstellung diese Entfernung entspricht (y;y). Das Verhältnis der Zahl der Gradeinstellung von y zu der von x ist das gesuchte Verhältnis.
16. Ein Gegenstand aus Metall ist gegeben, dessen Material, Gewicht und Ausmaße bekannt sind. Gesucht wird das nötige Gewicht eines anderen Metalls, um das gleiche Objekt mit denselben Ausmaßen herzustellen.
Gegeben ist eine Zinndose mit dem Gewicht von 36. Welches Gewicht in Silber braucht man, um die gleiche Dose herzustellen?
Man nimmt die Entfernung vom Zentrum des Zirkels bis zur Bezeichnung für Silber und überträgt sie auf die Gradeinstellung 36 auf der Linie der Körper.
Dann nimmt man die Entfernung vom Zentrum des Zirkels bis zum Symbol für Zinn und sucht auf der Linie der Körper, welche zwei identischen Gradeinstellungen dieser Entfernung entsprechen. Die Zahl dieser Gradeinstellungen ist das nötige Gewicht in Silber.
Der Proportionalzirkel erlaubt auch noch andere Operationen, wie beispielsweise:
-
das Segment einer Gerade zu finden, dessen Länge einem gegebenen Kreisumfang entspricht;
-
eine Gerade zu zeichnen, die zwei oder drei anderen proportional ist;
-
eine Figur zu zeichnen, die zwei anderen geometrisch ähnlich ist und deren Fläche der Differenz der Flächen der beiden anderen Figuren entspricht;
-
einen Würfel zu finden, dessen Volumen dem eines gegebenen Parallelflächners entspricht;
-
das Verhältnis zwischen den Gewichten zweier Körper zu finden, die geometrisch ähnlich sind, aber aus verschiedenen Metallen bestehen.
Drei Abbildungen aus einem Lehrbuch des 17. Jahrhunderts:
Der französische Kartograph und Ingenieur Allain Manesson Mallet (1630-1706), zunächst Kriegsbaumeister des portugiesischen Königs, zuletzt Mathematiklehrer am Hofe Ludwig des XIV, war einer der bedeutensten Fortifikationsingenieure seiner Zeit. Der erste Teil beschäftigt sich mit der Befestigung regelmäßiger und unregelmäßiger Plätze, der zweite Teil mit dem Bau der Fortifikationen und der dritte Teil mit Angriff und Verteidigung dieser Befestigungen.- Die Kupfer zeigen Befestigungen, Kriegsgerät oder Schlachtformationen, der Hintergrund jeweils eine klein Stadtansicht, darunter Amsterdam, Antwerpen, Budapest, Brest, Lissabon, Madrid, Neapel, Speyer, Venedig, Wien.


Abbildungen aus: 'Les Traveaux de Mars ou L'Art de
la Guerre'
(Die Arbeiten des Mars oder die Kunst des Krieges)
von Alain Manesson Mallet. Paris 1684 S. 39, 41 und 29
Die erste Abbildung beschreibt, wie man ein regelmäßiges Fünfeck mit Hilfe der Gradskala (Cordes) des Proportionalzirkels und eines gewöhnlichen Zirkels konstruiert: Zunächst rechnet man den Mittelpunktswinkel jeder Seite aus: 360° : 5 = 72°. Dann zeichnet einen Kreis und öffnet den Proportionalzirkel so weit, dass der Radius zwischen wie beiden 60°-Marken passt. Nun greift man mit dem Zirkel den Abstand der beiden 72°-Marken des Proportionalzirkels ab und markiert entlang der Kreislinie das Fünfeck.
Die Methode der zweiten Abbildung erfordert keine Rechnung. Der Radius des Kreises wird mit dem Zirkel gemessen. Dann wird der Proportionalzirkel so weit geöffnet, dass dieser Radius zwischen die beiden Markierungen "6" der Polygonskala passt. Nun wird der Zirkel so eingestellt, dass seine beiden Spitzen auf die beiden Markierungen "5" deuten. Mit diesem Abstand werden nun auf der Kreislinie die Ecken des Fünfecks abgetragen.
Die dritte Abbildung zeigt, dass man mithilfe der Linie "Parties Egales" eine gegebene Strecke in gleiche Teile aufteilen kann. Um eine Linie in drei gleiche Teile zu teilen, nimmt man sie in den Zirkel und legt sie im Proportionalzirkel zwischen die 9 des oberen und des unteren Schenkels. Der Abstand zwischen den beiden Markierungen mit der 3 ist das gesuchte Drittel.
Rechenwerkzeug.de